Лабораторная работа №1. Диаграммы растяжения пластичных материалов.
Цель работы:
изучить поведение малоуглеродистой стали при растяжении
определить ее механические характеристики.
определение работу упругих сил
Основные сведения
Для количественной оценки основных свойств материалов, как правило, экспериментально определяют диаграмму растяжения в координатах и . Для этого образцы испытывают в лаборатории на специальных машинах. Образцы для испытания на растяжение изготовляют в виде стерженей круглого или прямоугольного сечения. Образцы имеют на концах утолщения (головки). Размеры образцов установлены стандартом (рис.1.)
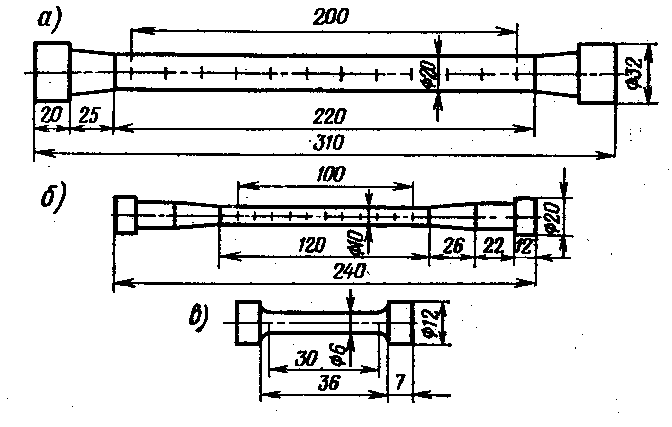
Рис 1.
Испытание дает возможность установить зависимость между растягивающей силой и удлинением бруса. Результат можно представить на графике, при построении которого по оси абцисс откладывают удлинение, по оси ординат -силу. График называются диаграммой растяжения (рис. 2.) На диаграмме отмечены характерные точки. Дадим их определение.
Наибольшее напряжение, до которого материал следует закону Гука, называется пределом пропорциональности п .
σп
=
(1)
В пределах закона Гука тангенс угла наклона прямой = f () к оси определяется величиной Е.
Упругие свойства материала сохраняются до напряжения У , называемого пределом упругости:
σу
=
(2)
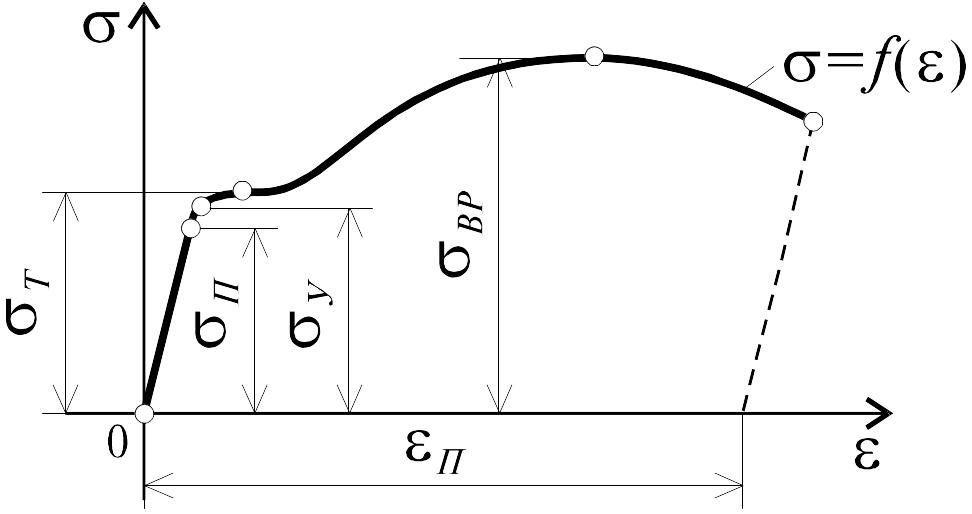
Рис2.
Под пределом упругости У понимается такое наибольшее напряжение, до которого материал не получает остаточных деформаций, т.е. после полной разгрузки последняя точка диаграммы совпадает с начальной точкой 0.
Величина т называется пределом текучести материала:
σт
=
(3)
Под пределом текучести понимается то напряжение, при котором происходит рост деформаций без заметного увеличения нагрузки. Если необходимо различать предел текучести при растяжении и сжатии Т соответственно заменяется на тр и тс . При напряжениях больших Т в теле конструкции развиваются пластические деформации П , которые не исчезают при снятии нагрузки.
Отношение максимальной силы, которую способен выдержать образец, к его начальной площади поперечного сечения носит название предела прочности, или временного сопротивления, и обозначается через, вc (при сжатии всс ).
σв
с
=
(4)
напряжение в точке разрыва равно:
бр
=
(5)
Относительное удлинение бруса:
δ
=
(6)
где l0 , l-длина бруса до и после деформации.
Относительное сужение бруса:
ψ
=
(7)
где А0 , А- площади поперечного сечения до и после деформации.
Относительное сужение бруса и удлинение (6), (7) бруса называются пластическими характеристиками материала. Напряжения (1) –(5) –прочностные или механические характеристики материалов.
При выполнении практических расчетов реальную диаграмму (рис. 2) упрощают, и с этой целью применяются различные аппроксимирующие диаграммы. Для решения задач с учетом упругопластических свойств материалов конструкций чаще всего применяется диаграмма Прандтля. По этой диаграмме напряжение изменяется от нуля до предела текучести по закону Гука = Е , а далее при росте , = Т (рис. 3.).
Способность материалов получать остаточные деформации носит название пластичности. На рис. 3. была представлена характерная диаграмма для пластических материалов.
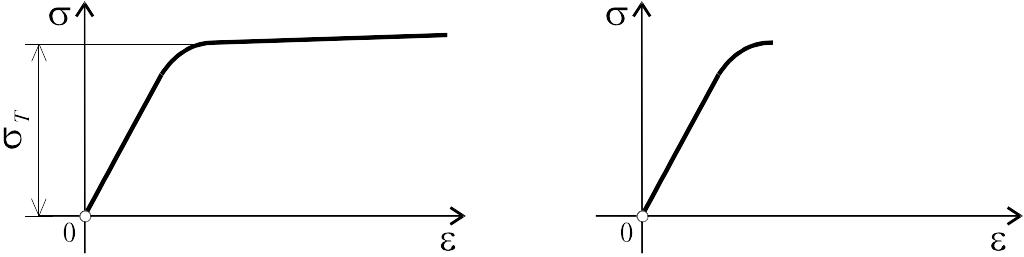
Рис. 3. Рис. 4
Противоположным свойству пластичности является свойство хрупкости, т.е. способность материала разрушаться без образования заметных остаточных деформаций. Материал, обладающий этим свойством, называется хрупким. К хрупким материалам относятся чугун, высокоуглеродистая сталь, стекло, кирпич, бетон, природные камни. Характерная диаграмма деформации хрупких материалов изображена на рис. 4.
Результаты работы.
1.Размеры образца:
до испытании: длина-l0 =
диаметр- d=
площадь сечения-A0=
объем- V=
после испытании: длина-l =
диаметр- d=
площадь сечения-A=
2. Построение диаграмму растяжения в координатах и .
3. Определение напряжения в характерных точках:
бпц=
=
бт=
=
бвс=
=
бр= =
Определение
работу упругих сил:
А=
=
Контрольные вопросы:
1.Что такое пластичность, прочность материалов?
2.Определение предела пропорциональности, предела упругости и предела текучести.
3.Что такое хрупкость и перечислите хрупкие материалы?