МІНІСТЕРСТВО ОСВІТИ І НАУКИ,

МОЛОДІ ТА СПОРТУ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

«ХАРКІВСЬКИЙ ПОЛІТЕХНИЧНИЙ ІНСТИТУТ»

Кафедра: «Обчислювальна техніка та програмування»

	ЗАТВЕРДЖУЮ Завідуючий кафедрою проф. Домнін Ф.О. (подпись, фамилия и инициалы) “ ” 2013 г.

ОБМЕЖЕНА ЗАДАЧА ПАКУВАННЯ ОБ’ЄКТІВ

Науково-дослідна робота

РОЗРОБНИКИ

Керівник проекту

____________/доц. Черних О.П./

“_____” _______________2013 г.

Консультант по НДРС

_______/проф. Дмитрієнко В.Д./

“_____” _______________2013 г.

Виконавець

студент группы КІТ-18м

______________/ Проценко Д.І./

“_____” _______________2013 г.

Харків 2013

ЗМІСТ

ВСТУП 3

1. ПОСТАНОВКА ЗАДАЧІ 5

1.1 «0-1» задача пакування рюкзаку 5

1.2 Обмежена задача пакування рюкзаку 6

1.3 NP- повнота задачі 6

2. МЕТОДИ РОЗВ’ЯЗАННЯ 8

2.1 Класифікація методів 8

2.2 Динамічне програмування 8

2.3 Повний перебір 9

2.4 Метод гілок і меж 10

2.5 Жадібний алгоритм 11

2.6 Порівняльна характеристика алгоритмів 11

ВИСНОВОК 14

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ 15

ВСТУП

Віртуалізація серверних ресурсів - технологія, що дозволяє побудувати і використовувати керовану, високонадійну, гнучку, безпечну і максимально ефективну ІТ-інфраструктуру.

Віртуалізація дозволяє розгорнути на одному фізичному сервері кілька віртуальних серверів , кожен з яких має власну операційну систему і набір сервісів. При цьому вирішується питання з недостатнім завантаженням існуючого обладнання, з'являються вільні ресурси для розгортання нових сервісів. Технології балансування навантаження і відмовостійкості дозволяють гарантувати високу доступність всіх інформаційних сервісів компанії. До того ж перехід у віртуальне середовище дозволяє заощадити на ліцензуванні операційних систем і сервісного програмного забезпечення, обслуговуванні парку серверного обладнання, що значно скорочується, системах кондиціонування та електроживлення.

Віртуальні машини можуть використовуватися для:

1. Захисту інформації та обмеження можливостей програм;

2. Дослідження продуктивності програмного забезпечення або нової комп'ютерної архітектури;

3. Емуляції різних архітектур;

4. Оптимізації використання ресурсів мейнфреймів та інших потужних комп'ютерів;

5. Тестування шкідливого коду для управління інфікованою системою;

6. Моделювання інформаційних систем з клієнт-серверної архітектурою на одній ЕОМ(емуляція комп'ютерної мережі за допомогою декількох віртуальних машин);

7. Спрощення управління кластерами(віртуальні машини можуть просто мігрувати з одного фізичної машини на іншу під час роботи);

8. Тестування і налагодження системного програмного забезпечення.

Технології віртуалізації роблять можливим «упаковку» всього сервера, – апаратних засобів, операційної системи, програм і конфігурацій, – в портативний пакет віртуальної машини. Безліч віртуальних серверів можуть працювати одночасно і незалежно на одному фізичному сервері. Це стає можливим тому, що шар віртуалізації, пропонований спеціалізованим програмним забезпеченням, з одного боку, надає кожному віртуального сервера повну апаратну конфігурацію, а з іншого, займається розподілом ресурсів фізичного сервера між віртуальними серверами.

Проте, існує одна суттєва проблема при використанні віртуального середовища – розміщення віртуальних машин всередині фізичного сервера, а надалі, в усьому дата центрі. Іншими словами – обмежена задача пакування об’єктів або «задача про рюкзак».

1. Постановка задачі

Задачу упаковки рюкзака можна визначити засобами математичного апарату. Нехай кожному об'єкту для упаковки відповідає індекс , який приймає значення від 1 до n . Числа і відповідають вазі та вартості об'єкта. Максимальна допустима маса, яку здатний витримати рюкзак, дорівнює .

1.1 «0-1» задача пакування рюкзаку

Існує багато варіантів заповнення рюкзака. Для описання такого типу задач для кожного об’єкту необхідно вказати, обраний він або ні. Для цього можна використовувати двійковий вектор , компонента якого дорівнює 1, якщо -тий об'єкт запаковано, і 0 якщо ні. Цей вектор називається вектором заповнення. Вага та вартість запакованих предметів, можна обчислити як функцію від вектора заповнення.

Для заданого вектора заповнення X вартість предметів упакованих в рюкзак дорівнює:

(1)

За аналогією, загальна маса предметів дорівнює:

(2)

Таким чином завдання пакування рюкзаку полягає у знаходженні такого вектора заповнення , котрий максимізує функцію  за умови:

(3),

тобто, загальна маса обраних предметів не перевищує місткості рюкзаку .

Але існують певні додаткові умови:

– загальна вага всіх предметів більша за місткість рюкзаку;

– вартість предмета – натуральне число;

– будь-який об’єкт займає ресурси.

Припустимо, крім вартості предмети мають ще одну характеристику (наприклад, щільність). Завдання пошуку вектора заповнення X, який максимізує обидві функції (сумарна вартість і сумарна щільність) є багатокритеріальним варіантом «0-1» задачі пакування рюкзака.

1.2 Обмежена задача пакування рюкзаку

Обмежує кількість копій кожного виду предметів максимальним цілим значення . Математично цю задачу можна описати так: максимізувати за умов:

1. ;

2. 

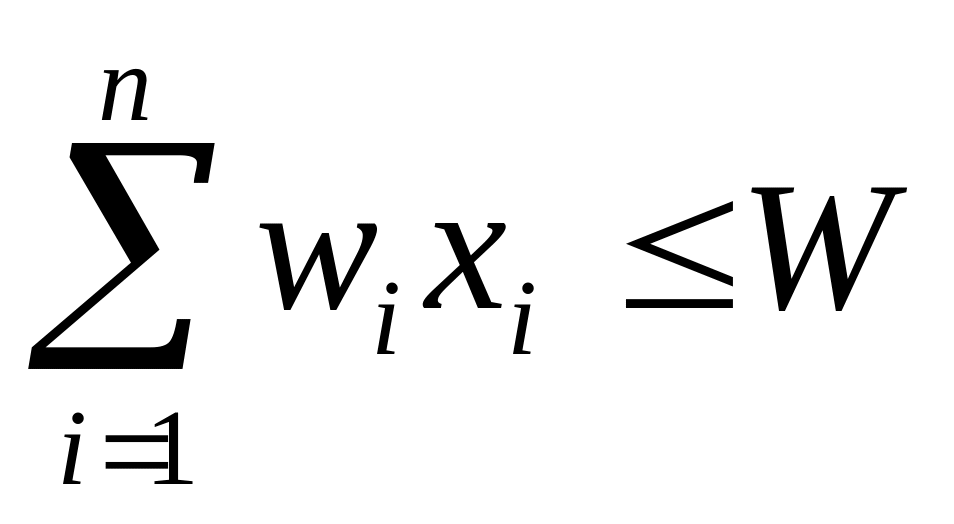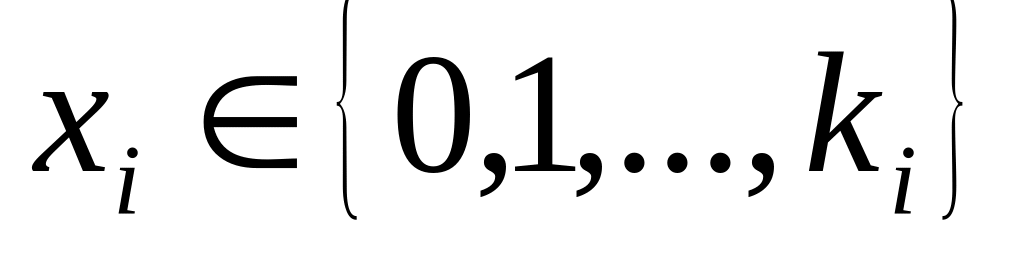
1.3 NP- повнота задачі

Зустрічаються задачі , які не можна розв’язати за поліноміальний час. Це клас NP- повних задач. Деякі задачі цього класу на перший погляд аналогічні задачам, які розв'язуються за поліноміальний час, але це далеко не так. Задача називається NP- повною, якщо для неї не існує поліноміального алгоритму. Алгоритм називається поліноміальним , якщо його складність O (N) в гіршому випадку обмежена зверху деяким многочленом (поліномом) від N. Такі задачі виникають дуже часто в різних галузях: в булевій логіці, в теорії графів, теорії множин, кодуванні інформації, в алгебрі, в біології, фізиці, економіці, теорії автоматів і мов. Вважається що NP- повні задачі дуже важко розв’язуються, а також, якщо хоча б для однієї з них вдасться знайти поліноміальний алгоритм , то такий алгоритм буде існувати для будь-якої задачі з цього класу. Над пошуком поліноміальних алгоритмів до таких завдань трудилися багато вчених, і все ж і при такому розмаїтті NP- повних задач, ні для однієї з них до цих пір не знайдено поліноміального алгоритму. З усього вищесказаного випливає , що якщо відома NP- повнота задачі, то краще витратити час на побудову наближеного алгоритму, ніж намагатися побудувати поліноміальний, або ж, якщо це дозволяють умови, використовувати алгоритми з експоненціальною складністю роботи.