4.2.4. Интерференция света в тонких пленках.

В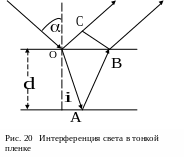 есьма распространенным случаем интерференции является интерференция световых лучей, отраженных от двух поверхностей прозрачной пластины (масляные пятна на воде, мыльные пузыри, оксидные пленки и т.д.).

Пусть на плоскопараллельную пластинку в точке О падает луч света (рис. 20). В этой точке он разделится на два - отраженный и преломленный. Преломленный луч после отражения в точке А и преломления в точка В снова выходит в воздух. Лучи 1 и 2 отраженные от верхней и нижней поверхности пластинки, когерентны между собой. Если на их пути поставить собирающую линзу, то они сойдутся в некоторой точке фокальной плоскости линзы и дадут интерференционную картину, которая определяется оптической разностью хода между этими лучами.

Оптическая разность хода лучей (как видно из рисунка 20)

, 2.8

где - показатель преломления пленки, а слагаемое обусловлено потерей полуволны при отражении света от оптически более плотной среды. Если показатель преломления среды , то потеря полуволны происходит в точке О и берется знак , в противном случае потеря полуволны происходит в точке А и берется знак .

Учитывая закон преломления света легко показать, что

, 2.9

где - толщина пленки, - угол падения луча.

Из полученного выражения следует, что при заданных , интерференционная картина зависит от .

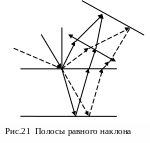
1. Полосы равного наклона. При постоянной толщине пленки разность хода волн зависит от угла падения лучей на пленку. Интерференционная картина, возникающая в результате интерференции лучей, падающих на пленку под различными углами, получила название полос равного наклона. Полосы равного наклона локализованы в бесконечности и поэтому для их наблюдения используют собирающую линзу, а экран располагают в ее фокальной плоскости. Если оптическая ось линзы перпендикулярна плоскости пластины, то линии равного наклона будут иметь вид концентрических окружностей с центром в фокусе линзы.

2. Полосы равной толщины. Рассмотрим отражение света от прозрачной пластины, поверхности которой не параллельны между собой (тонкий клин). В этом случае также появятся два луча, отраженные от верхней и нижней поверхности клина, но эти лучи не будут параллельными, а пересекаются в точке В, вблизи поверхности клина. Поэтому говорят, что полосы равной толщины локализованы на поверхности клина. При малых значениях угла клина оптическую разность хода волн можно найти по той же формуле 2.9. Если на пути лучей поставить собирающую линзу, то они будут интерферировать.

Лучи, падающие в другую точку клина под тем же самым углом, будут собираться линзой в другой точке. Оптическая разность хода волн будет определяться уже другой толщиной пленки. Таким образом, на экране возникает система интерференционных полос. Каждая из полос возникает за счет отражения света от мест пластинки, имеющих одинаковую толщину и поэтому называется полосой равной толщины.

К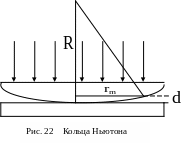 ольца Ньютона. Классическим примером полос равной толщины являются кольца Ньютона, наблюдающиеся при отражении света от тонкого воздушного клина, образованного плоско параллельной стеклянной пластиной и соприкасающейся с ней плоско выпуклой линзой с большим радиусом кривизны. При нормальном падении света луч отражается от верхней и нижней поверхности клина и при наложении этих лучей образуется интерференционная картина, имеющая вид концентрических колец.

В отраженном свете оптическая разность хода волн будет определяться толщиной воздушного клина в месте отражения луча и потерей полуволны при отражении от нижней границы клина (показатель преломления стекла больше показателя преломления воздуха), т.е.

. 2.10

Из рисунка следует, что . Пренебрегая величиной второго порядка малости можно получить, что и тогда

. 2.11

Подставляя в условие интерференционного минимума 2.4, найдем радиус темных колец Ньютона

. 2.12

Из полученного выражения 2.12 следует, что зависит от длины волны и поэтому при освещении линзы белым светом наблюдается система радужных колец.

Зная радиус кривизны линзы, и измеряя радиус колец Ньютона на опыте можно определить длину световой волны.