
- •Главные этапы в развитии теории света
- •1.4. Геометрическая оптика
- •Законы распространения света.
- •2.1.4. Преломление света на сферической поверхности.
- •3.1.4. Тонкие линзы. Формула тонкой линзы.
- •4.1.4. Аберрации линз.
- •Оптические приборы.
- •Задачи к зачету
- •2.2. Интерференция света
- •1.2.4. Интерференция света. Условия образования интерференционного максимума и минимума.
- •2.2.4. Методы наблюдения интерференции света
- •3.2.4. Расчет интерференционной картины от двух источников.
- •4.2.4. Интерференция света в тонких пленках.
- •5.2.4. Применение интерференции. Интерферометры.
- •Задачи к зачету
- •3.4. Дифракция света
- •1.3.4. Принцип Гюйгенса.
- •2.3.4. Метод зон Френеля. Закон прямолинейного распространения света.
- •3.3.4. Дифракция Френеля на круглом отверстии и диске.
- •4.3.4. Дифракция Фраунгофера (дифракция в параллельных лучах).
- •5.3.4. Дифракционная решетка
- •6.3.4. Разрешающая способность оптических приборов.
- •Задачи к зачету
- •4.4. Поляризация света.
- •1.4.4. Естественный и поляризованный свет
- •2.4.4. Поляризация света при отражении и преломлении света.
- •3.4.4. Двойное лучепреломление
- •4.4.4. Поляризационные призмы и поляроиды.
- •5.4.4. Искусственная оптическая анизотропия
- •6.4.4. Вращение плоскости поляризации.
- •Задачи к зачету
- •5.4. Элементы теории относительности.
- •1.5.4. Скорость света и ее опытное определение.
- •2.5.4. Принцип относительности Галилея и законы электродинамики
- •2.5.4. Преобразования Лоренца.
- •3.5.4. Следствия из преобразований Лоренца.
- •1. Относительность одновременности.
- •2. Относительность промежутков времени.
- •3. Относительность длин отрезков.
- •4. Релятивистский закон сложения скоростей.
- •5. Интервал между событиями.
- •6.4. Тепловое излучение.
- •1.6.4. Тепловое излучение и его характеристики
- •2.6.4. Закон Кирхгофа. Универсальная функция Кирхгофа.
- •3.6.4. Законы Стефана – Больцмана и смещения Вина.
- •4.6.4. Формулы Релея – Джинса, Вина и Планка
- •4.6.4. Оптическая пирометрия.
- •Задачи к зачету
- •7.4. Квантовые свойства света.
- •1.7.4. Явление фотоэффекта и его законы.
- •2. Максимальная кинетическая энергия фотоэлектронов пропорциональна частоте падающего излучения.
- •3. Существует красная граница фотоэффекта, т.Е. Минимальная частота света, при которой свет любой интенсивности фотоэффекта не вызывает.
- •2.7.4. Уравнение Эйнштейна для фотоэффекта. Фотон.
- •3.7.4. Эффект Комптона и его объяснение на основе квантовых представлений.
- •4.7.4. Фотон. Масса и импульс фотона. Давление света.
- •Задачи к зачету
- •8.4. Теория атома водорода.
- •1.8.4. Спектр атома водорода
- •2.8.4. Атом водорода по Бору.
- •3.8.4. Рентгеновское излучение.
- •4.8.4. Поглощение, спонтанное и вынужденное излучение. Лазеры.
- •9.4. Элементы квантовой механики.
- •1.9.4. Корпускулярно - волной дуализм.
- •2.9.4. Соотношение неопределенностей Гейзенберга
- •3.9.4. Волновая функция и ее статистический смысл.
- •4.9.4. Уравнение Шредингера.
- •5.9.4. Частица в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками.
- •5.9.4. Гармонический осциллятор в квантовой механике.
- •6.9.4. Атом водорода в квантовой механике.
- •Задачи к зачету
- •10.4. Элементы физики атомного ядра.
- •1.10.4. Открытие нейтрона. Строение атомного ядра.
- •2.10.4. Дефект масс. Энергия связи атомного ядра.
- •3.10.4. Радиоактивное излучение и его состав.
- •5.10.4. Ядерные реакции и их основные типы.
Задачи к зачету
Линза, расположенная между предметом и экраном дает, дает на экране увеличенное изображение предмета. Когда линзу передвинули на 40 см ближе к экрану, на нем появилось четкое уменьшенное изображение предмета. Определить фокусное расстояние линзы, если расстояние между предметом и экраном равно 80 см.
Каково наименьшее возможно расстояние между предметом и его действительным изображением, создаваемым собирающей линзой с фокусным расстоянием 12 см?
Доказать, что оптическая сила системы сложенных вместе тонких линз равна алгебраической сумме оптических сил каждой из этих линз.
У линзы находящейся в воздухе фокусное расстояние равно 5 см, а погруженной в раствор сахара 35 см. Определить показатель преломления раствора сахара.
Определить оптическую силу выпукло-вогнутой линзы с радиусами кривизны 1 м и 40 см, изготовленной из стекла с показателем преломления 1,5.
Определить радиусы кривизны выпукло-вогнутой линзы, если известно, что один из них в три раза больше другого, а оптическая сила линза равна 8 дптр.
Два плоских зеркала образуют двугранный угол
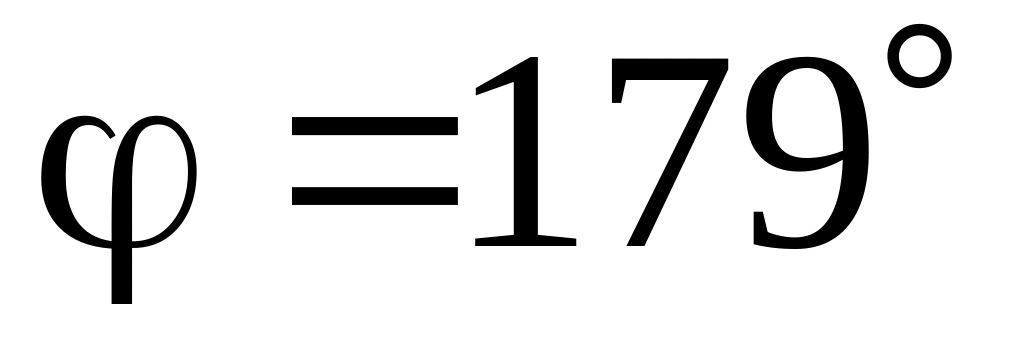 .
На расстоянии
.
На расстоянии
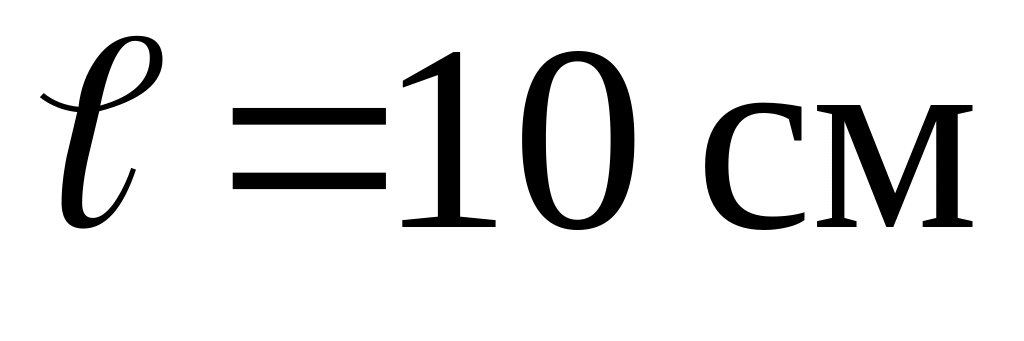 от линии соприкосновения зеркал и на
одинаковом расстоянии от каждого
зеркала находится точечный источник
света. Определить расстояние между
мнимыми изображениями источника в
зеркалах.
от линии соприкосновения зеркал и на
одинаковом расстоянии от каждого
зеркала находится точечный источник
света. Определить расстояние между
мнимыми изображениями источника в
зеркалах.Пучок параллельных лучей падает на толстую стеклянную пластинку под углом
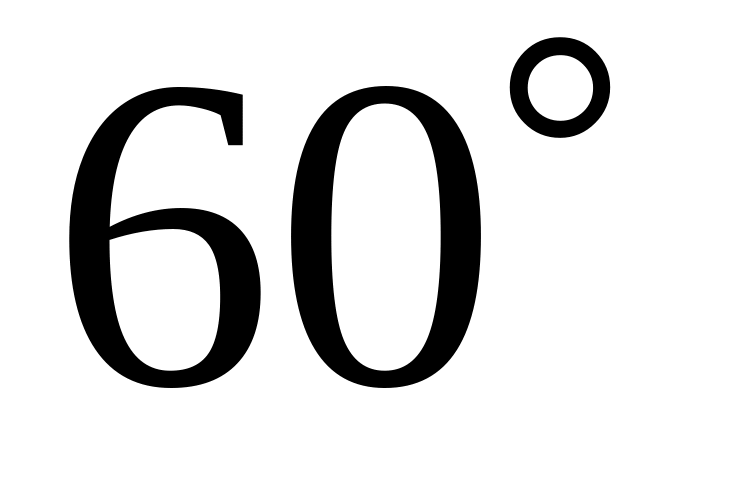 ,
и, преломляясь, переходит в стекло.
Ширина пучка в воздухе равна 10 см.
Определить ширину пучка в стекле, если
показатель преломления стекла равен
1,5.
,
и, преломляясь, переходит в стекло.
Ширина пучка в воздухе равна 10 см.
Определить ширину пучка в стекле, если
показатель преломления стекла равен
1,5.Луч света переходит из среды с показателем преломления
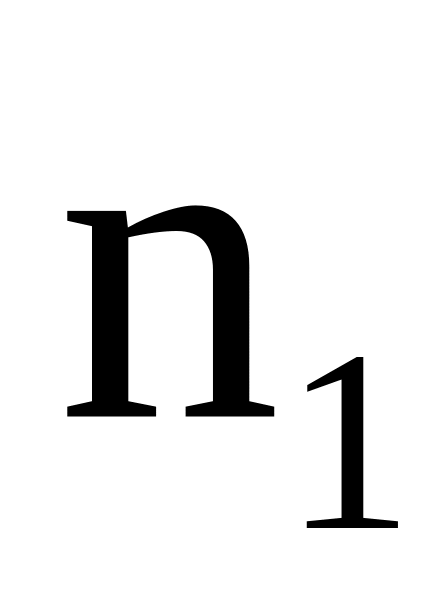 в среду с показателем
в среду с показателем
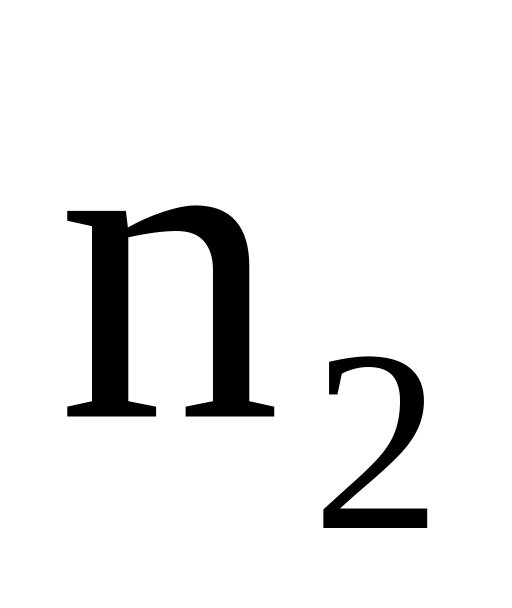 .
Показать, что если отраженный и
преломленный лучи взаимно перпендикулярны,
то выполняется условие
.
Показать, что если отраженный и
преломленный лучи взаимно перпендикулярны,
то выполняется условие
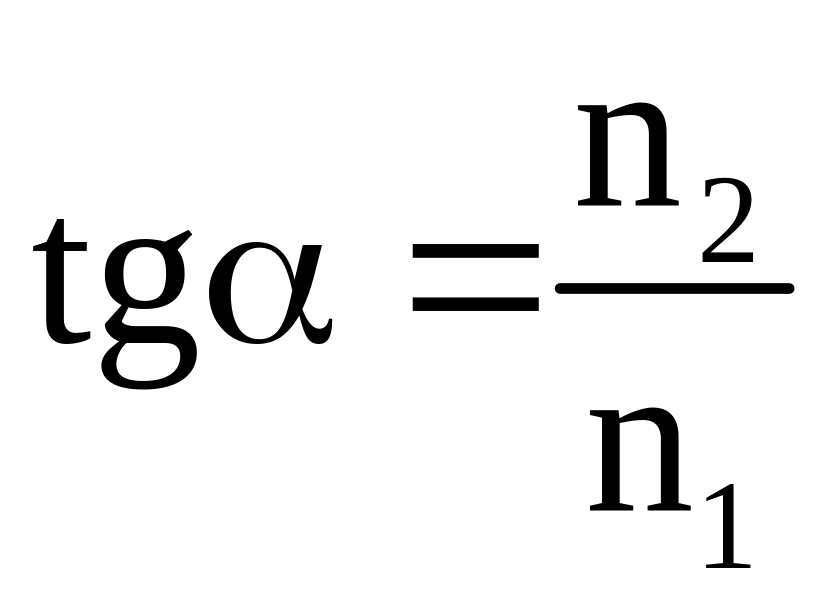 ,
где
- угол падения луча.
,
где
- угол падения луча.Отношение радиусов кривизны поверхностей линзы равно 2. Определить радиус кривизны выпуклой поверхности линзы, если оптическая сила линзы равна 10 дптр.
Определить радиус кривизны выпуклой поверхности линзы, если при отношении радиусов кривизны поверхностей линзы, равном 3, ее оптическая сила равна – 8 дптр.
Линза изготовлена из стекла, показатель преломления которого для красных лучей 1,50, а для фиолетовых 1,52. Радиусы кривизны поверхностей линзы одинаковы и равны 1 м. Определить разность фокусных расстояний линзы для красных и фиолетовых лучей.
Фокусное расстояние собирающей линзы в воздухе равно 10 см. Определить чему оно будет равно в воде, если показатель преломления стекла равен 1,5, а воды 1,33.
Человек без очков читает книгу, располагая ее на расстоянии 12,5 см от глаза. Какой оптической силы очки ему надо носить?
2.2. Интерференция света
1.2.4. Интерференция света. Условия образования интерференционного максимума и минимума.
Для описания световой волны можно
воспользоваться уравнением гармонических
колебаний
![]() ,
где под
,
где под
![]() понимают напряженность электрического
понимают напряженность электрического
![]() или магнитного
или магнитного
![]() полей волны. И тогда интерференцию света
можно объяснить рассматривая сложение
колебаний.
полей волны. И тогда интерференцию света
можно объяснить рассматривая сложение
колебаний.
Ранее мы показали, что при сложении двух
гармонических колебаний одного периода
происходящих по одному направлению
![]() и
и
![]() ,
получается вновь гармоническое колебание
того же периода
,
получается вновь гармоническое колебание
того же периода
![]() ,
амплитуда А которого определяется из
соотношения
,
амплитуда А которого определяется из
соотношения
![]() 2.1
2.1
Из данного выражения следует, что квадрат
амплитуды результирующего колебания
не равняется сумме квадратов амплитуд
складываемых колебаний, т.е. интенсивность
результирующего колебания не равна
сумме интенсивностей складываемых
колебаний. Так как интенсивность волны
![]() ,
то можно написать
,
то можно написать
![]() .
2.2
.
2.2
Отсюда следует, что в тех точках
пространства где
![]()
![]() ,
а там где
,
а там где
![]()
![]() .
В частности, при
.
В частности, при
![]() будем иметь
будем иметь
![]() при
при
![]() и
и
![]() при
при
![]() .
.
Следовательно, при наложении двух колебаний происходит пространственное перераспределение энергии колебаний, в результате чего в одних точках возникают максимумы, а в других минимумы колебаний. Это явление и называют интерференцией света.
Однако нужно иметь в виду тот факт, что
полученный результат будет иметь место
только в том случае, если разность фаз
складываемых колебаний
![]() не меняется с течением времени. Такие
волны называются когерентными.
не меняется с течением времени. Такие
волны называются когерентными.
Этому условию удовлетворяют так называемые монохроматические волны – не ограниченные в пространстве и во времени волны одной строго определенной частоты и постоянной амплитуды.
Если же разность фаз складываемых
колебаний беспорядочно меняется во
времени, то интенсивность результирующего
колебания будет равна сумме интенсивностей
складываемых колебаний, так как в этом
случае среднее значение разности фаз
![]() и, следовательно,
и, следовательно,
![]() и
и
![]() .
Колебания в этом случае называются не
когерентными. Поэтому мы не наблюдаем
интерференции света от двух независимых
источников света (например, от двух
электрических лампочек).
.
Колебания в этом случае называются не
когерентными. Поэтому мы не наблюдаем
интерференции света от двух независимых
источников света (например, от двух
электрических лампочек).
Объяснить это можно следующим образом.
Процесс излучения света атомом конечен
и длится очень короткое время (![]() ).
Через некоторое время атом может снова
возбудиться и начать испускать световые
волны, но уже с другой начальной фазой.
В двух независимых источниках света
атомы излучают свет независимо друг от
друга и в результате этого волны,
излучаемые ими, не будут являться
когерентными.
).
Через некоторое время атом может снова
возбудиться и начать испускать световые
волны, но уже с другой начальной фазой.
В двух независимых источниках света
атомы излучают свет независимо друг от
друга и в результате этого волны,
излучаемые ими, не будут являться
когерентными.
Поэтому для наблюдения интерференции света применяют метод разделения волны излучаемой одним источником, на две части, которые после прохождения различных оптических путей накладываются друг на друга.
Пусть в точке О, где происходит разделение,
волна описывается уравнением
![]() .
До точки М, в которой наблюдается
интерференция, первая волна в среде с
показателем преломления
.
До точки М, в которой наблюдается
интерференция, первая волна в среде с
показателем преломления
![]() проходит расстояние
проходит расстояние
![]() и она будет описываться уравнением
и она будет описываться уравнением
 .
Вторая волна в среде с показателем
преломления
.
Вторая волна в среде с показателем
преломления
![]() проходит расстояние
проходит расстояние
![]() и описывается уравнением
и описывается уравнением
 .
Здесь мы учли, что
.
Здесь мы учли, что
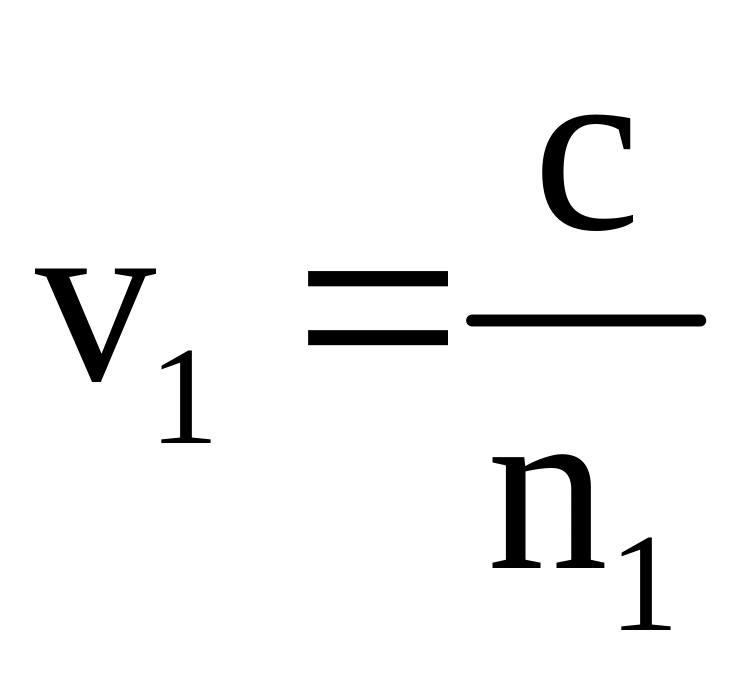 и
и
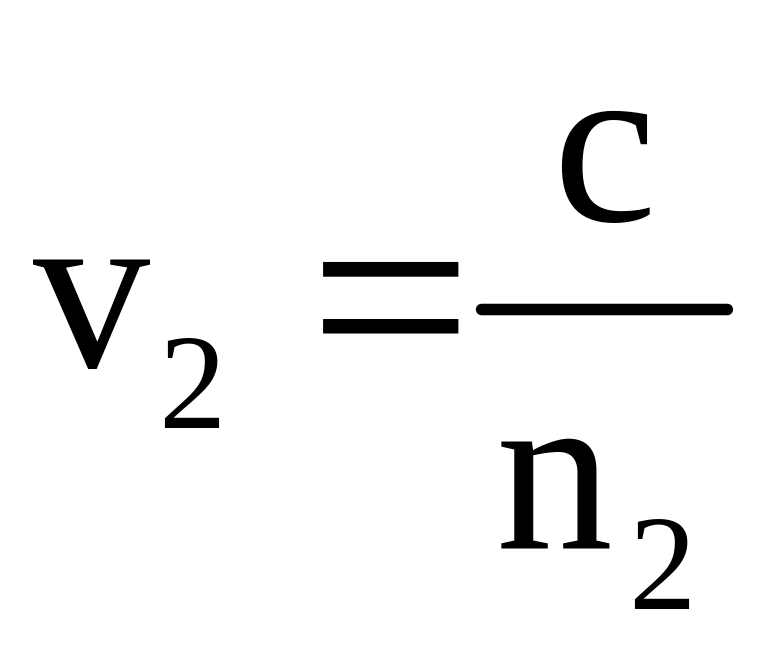 Следовательно, разность фаз
Следовательно, разность фаз
![]() .
Обозначим
.
Обозначим
![]() и будем называть эту величину оптическим
ходом волны. Учитывая, что
и будем называть эту величину оптическим
ходом волны. Учитывая, что
![]() ,
где
,
где
![]() -
длина световой волны в вакууме, получим
-
длина световой волны в вакууме, получим
![]() ,
где
,
где
![]() оптическая разность хода волн.
оптическая разность хода волн.
Если
![]() ,
то
,
то
![]() и в этой точке будет наблюдаться максимум
интерференции. Подставляя это условие
в найденное значение разности фаз
складываемых колебаний, получим условие
наблюдения интерференционного максимума
и в этой точке будет наблюдаться максимум
интерференции. Подставляя это условие
в найденное значение разности фаз
складываемых колебаний, получим условие
наблюдения интерференционного максимума
![]()
![]() .
2.3
.
2.3
Максимум интерференции наблюдается в том случае, если оптическая разность хода волн равна четному числу полуволн или целому числу длин волн.
Если же
![]() ,
то
,
то
![]()
![]() 2.4
2.4
- условие наблюдения интерференционного минимума.
