
- •Главные этапы в развитии теории света
- •1.4. Геометрическая оптика
- •Законы распространения света.
- •2.1.4. Преломление света на сферической поверхности.
- •3.1.4. Тонкие линзы. Формула тонкой линзы.
- •4.1.4. Аберрации линз.
- •Оптические приборы.
- •Задачи к зачету
- •2.2. Интерференция света
- •1.2.4. Интерференция света. Условия образования интерференционного максимума и минимума.
- •2.2.4. Методы наблюдения интерференции света
- •3.2.4. Расчет интерференционной картины от двух источников.
- •4.2.4. Интерференция света в тонких пленках.
- •5.2.4. Применение интерференции. Интерферометры.
- •Задачи к зачету
- •3.4. Дифракция света
- •1.3.4. Принцип Гюйгенса.
- •2.3.4. Метод зон Френеля. Закон прямолинейного распространения света.
- •3.3.4. Дифракция Френеля на круглом отверстии и диске.
- •4.3.4. Дифракция Фраунгофера (дифракция в параллельных лучах).
- •5.3.4. Дифракционная решетка
- •6.3.4. Разрешающая способность оптических приборов.
- •Задачи к зачету
- •4.4. Поляризация света.
- •1.4.4. Естественный и поляризованный свет
- •2.4.4. Поляризация света при отражении и преломлении света.
- •3.4.4. Двойное лучепреломление
- •4.4.4. Поляризационные призмы и поляроиды.
- •5.4.4. Искусственная оптическая анизотропия
- •6.4.4. Вращение плоскости поляризации.
- •Задачи к зачету
- •5.4. Элементы теории относительности.
- •1.5.4. Скорость света и ее опытное определение.
- •2.5.4. Принцип относительности Галилея и законы электродинамики
- •2.5.4. Преобразования Лоренца.
- •3.5.4. Следствия из преобразований Лоренца.
- •1. Относительность одновременности.
- •2. Относительность промежутков времени.
- •3. Относительность длин отрезков.
- •4. Релятивистский закон сложения скоростей.
- •5. Интервал между событиями.
- •6.4. Тепловое излучение.
- •1.6.4. Тепловое излучение и его характеристики
- •2.6.4. Закон Кирхгофа. Универсальная функция Кирхгофа.
- •3.6.4. Законы Стефана – Больцмана и смещения Вина.
- •4.6.4. Формулы Релея – Джинса, Вина и Планка
- •4.6.4. Оптическая пирометрия.
- •Задачи к зачету
- •7.4. Квантовые свойства света.
- •1.7.4. Явление фотоэффекта и его законы.
- •2. Максимальная кинетическая энергия фотоэлектронов пропорциональна частоте падающего излучения.
- •3. Существует красная граница фотоэффекта, т.Е. Минимальная частота света, при которой свет любой интенсивности фотоэффекта не вызывает.
- •2.7.4. Уравнение Эйнштейна для фотоэффекта. Фотон.
- •3.7.4. Эффект Комптона и его объяснение на основе квантовых представлений.
- •4.7.4. Фотон. Масса и импульс фотона. Давление света.
- •Задачи к зачету
- •8.4. Теория атома водорода.
- •1.8.4. Спектр атома водорода
- •2.8.4. Атом водорода по Бору.
- •3.8.4. Рентгеновское излучение.
- •4.8.4. Поглощение, спонтанное и вынужденное излучение. Лазеры.
- •9.4. Элементы квантовой механики.
- •1.9.4. Корпускулярно - волной дуализм.
- •2.9.4. Соотношение неопределенностей Гейзенберга
- •3.9.4. Волновая функция и ее статистический смысл.
- •4.9.4. Уравнение Шредингера.
- •5.9.4. Частица в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками.
- •5.9.4. Гармонический осциллятор в квантовой механике.
- •6.9.4. Атом водорода в квантовой механике.
- •Задачи к зачету
- •10.4. Элементы физики атомного ядра.
- •1.10.4. Открытие нейтрона. Строение атомного ядра.
- •2.10.4. Дефект масс. Энергия связи атомного ядра.
- •3.10.4. Радиоактивное излучение и его состав.
- •5.10.4. Ядерные реакции и их основные типы.
6.9.4. Атом водорода в квантовой механике.
Решение задачи об энергетических уровнях электрона в атоме водорода сводится к решению задачи о движении электрона в кулоновском поле ядра.
Потенциальная энергия взаимодействия электрона с ядром определяется выражением
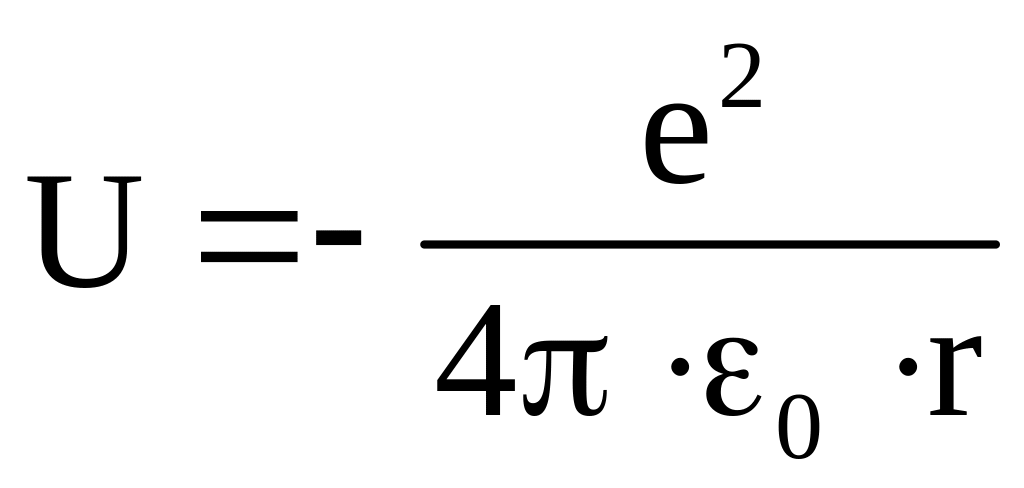 .
.
Следовательно, состояние электрона в
атоме водорода описывается функцией
![]() ,
удовлетворяющей уравнению Шредингера
в виде
,
удовлетворяющей уравнению Шредингера
в виде
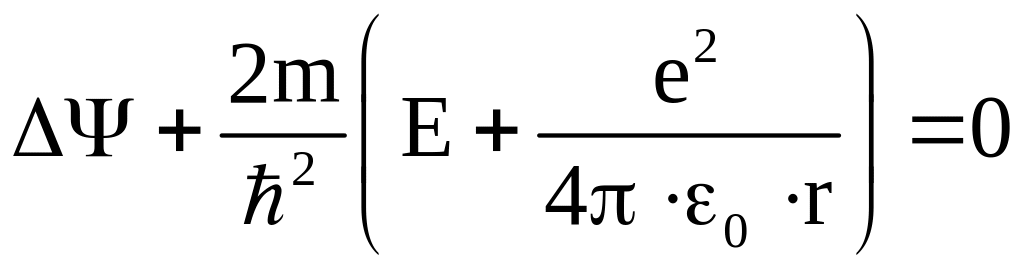 .
.
Мы уже указывали, что подобное дифференциальное уравнение имеет решение только при определенных значениях параметра Е. Как показывают расчеты
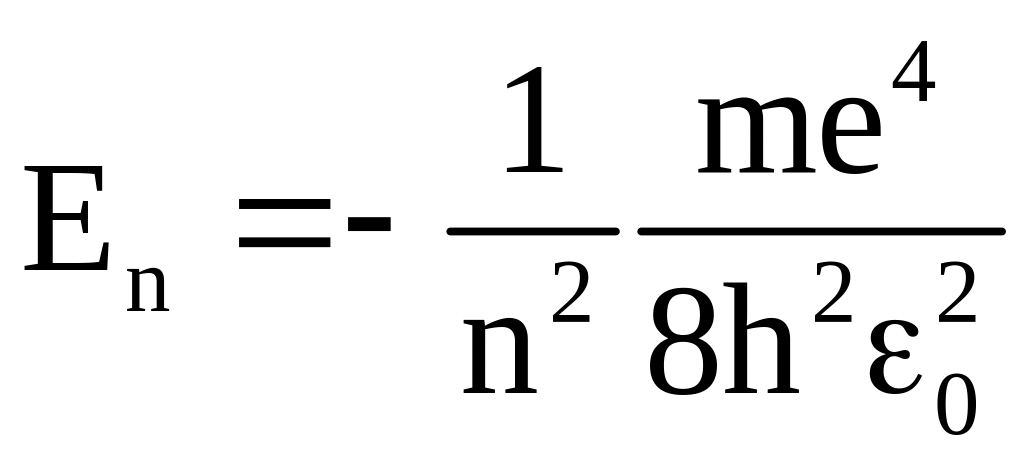 .
.
Легко заметить, что полученное решение совпадает со значением полученным Бором, но Бор вынужден был вводить дополнительные гипотезы, а в квантовой механике это результат самой теории, вытекающий из решения уравнения Шредингера.
Задачи к зачету
Электрон движется со скоростью
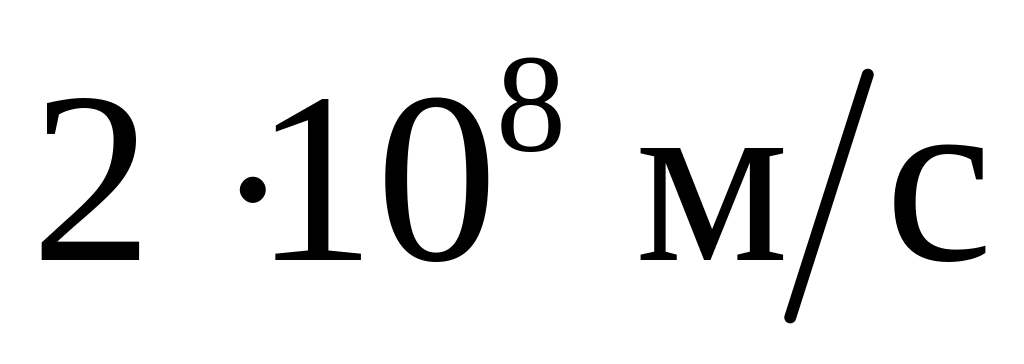 .
Определить длину волны де Бройля для
электрона, учитывая зависимость массы
от скорости.
.
Определить длину волны де Бройля для
электрона, учитывая зависимость массы
от скорости.Какую ускоряющую разность потенциалов должен пройти электрон, чтобы длина волны де Бройля была равна 0,1 нм?
Найти длину волны де Бройля протона, прошедшего ускоряющую разность потенциалов 1 МВ.
Предполагая, что неопределенность координаты движущейся частицы равна дебройлеровской длине волны, определить относительную неопределенность
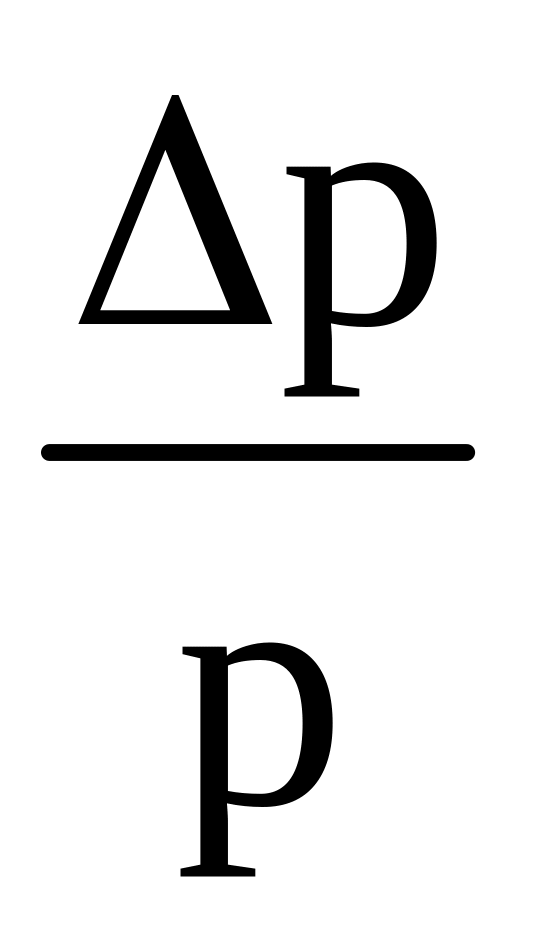 импульса частицы.
импульса частицы.Электрон находится в потенциальной яме шириной в возбужденном состоянии
 .
Определить в каких точках интервала
.
Определить в каких точках интервала
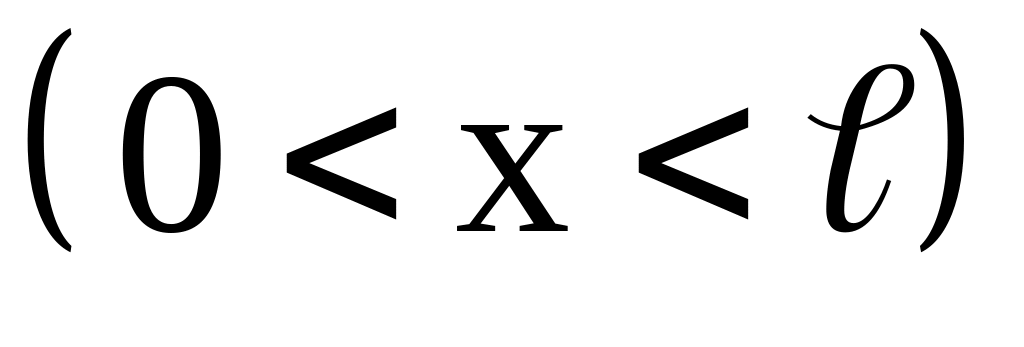 плотность вероятности нахождения
частицы минимальна?
плотность вероятности нахождения
частицы минимальна?Электрон находится в потенциальной яме шириной в возбужденном состоянии . Определить в каких точках интервала плотность вероятности нахождения частицы максимальна?
Электрон в одномерной потенциальной яме шириной находится в возбужденном состоянии . Определить вероятность обнаружения частицы в области
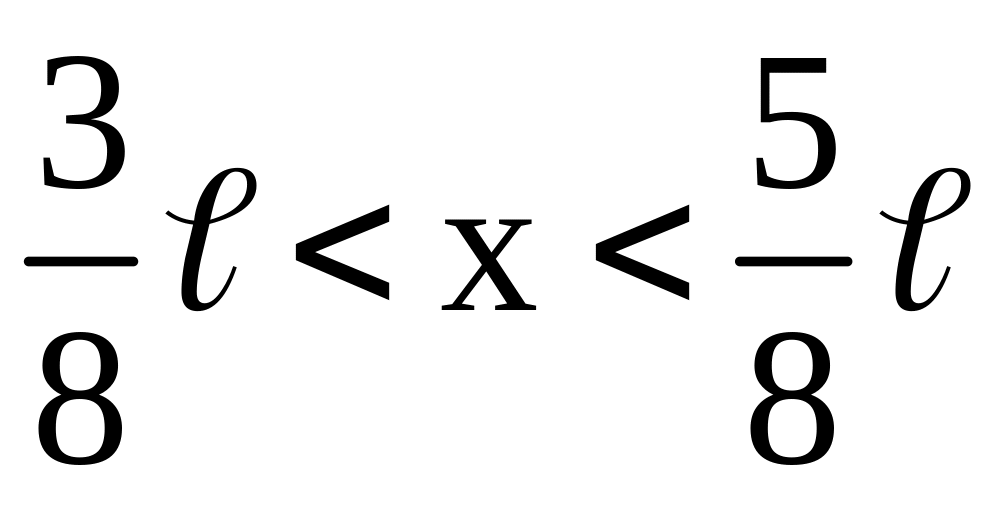 .
.Электрон в одномерной потенциальной яме шириной находится в возбужденном состоянии
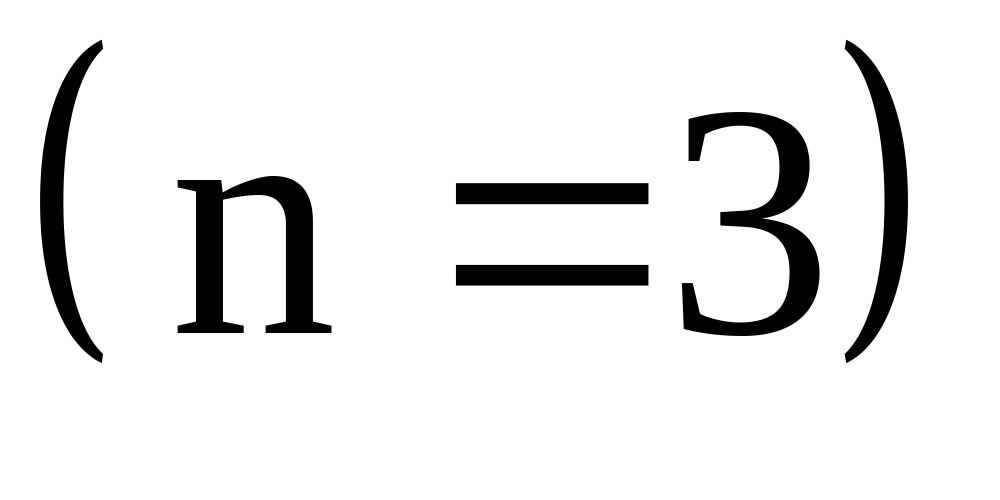 .
Определить вероятность обнаружения
частицы в области
.
Определить вероятность обнаружения
частицы в области
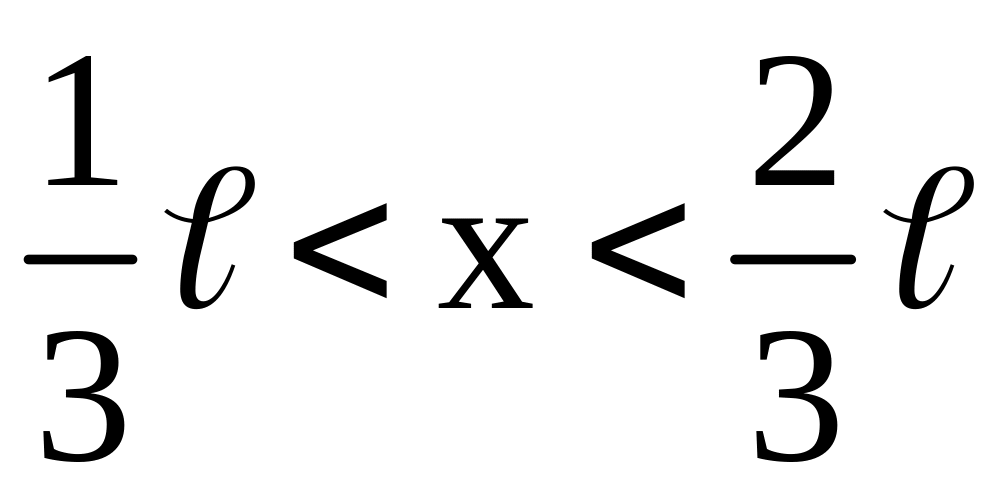 .
.
10.4. Элементы физики атомного ядра.
1.10.4. Открытие нейтрона. Строение атомного ядра.
В 1920 году Э.Резерфорд в камере Вильсона наблюдал первую ядерную реакцию
![]() 10.1
10.1
в результате которой образовывался протон.
В 1930 году В.Боде и Г. Беккер облучая ряд
элементов обнаружили, что при облучении
бериллия
-
частицами возникает излучение большой
проникающей способности, но не оставляющей
следов в камере Вильсона. Так как большой
проникающей способностью могут обладать
только нейтральные частицы, то было
высказано предположение о том, что это
кванты электромагнитного излучения.
Однако измерение энергии
![]() -
квантов проведенное Ирен и Фредериком
Жолио-Кюри показало, что они должны были
обладать невероятной энергией, порядка
50 МэВ, вместо расчетных 7 Мэв.
-
квантов проведенное Ирен и Фредериком
Жолио-Кюри показало, что они должны были
обладать невероятной энергией, порядка
50 МэВ, вместо расчетных 7 Мэв.
В 1932 году Д.Чедвик вначале предположил, а затем и доказал, что при бомбардировке бериллия образуются нейтральные частицы, которые он назвал нейтронами. Таким образом, при бомбардировке бериллия протекает ядерная реакция
![]() .
10.2
.
10.2
По своим характеристикам (кроме электрического заряда) нейтрон подобен протону и поэтому для этих частиц используется общее название нуклон.
Открытие нейтрона позволило Д.И.Иваненко
и Гейзенбергу высказать гипотезу о
строении атомного ядра. Так как заряд
ядра равен
(
-
атомный номер элемента), то в его состав
должно входить
протонов и число нейтронов равное
![]() (А – массовое число, число нуклонов в
ядре).
(А – массовое число, число нуклонов в
ядре).
Поскольку нейтроны не участвуют в электромагнитном взаимодействии, а протоны отталкиваются друг от друга, то необходимо было ответить на вопрос о стабильности ядра.
В ядре между нуклонами действуют особые, специфические силы, называемые ядерными силами. Закон ядерных сил не установлен, но установлены их основные свойства:
- ядерные силы являются силами притяжения;
- эти силы являются короткодействующими
– радиус действия
![]() ;
;
- ядерным силам свойственна зарядовая независимость (действуют между протонами и нейтронами);
- им свойственно насыщение, т.е. каждая частица может взаимодействовать с определенным числом соседей;
- ядерные силы не являются центральными.
Сложный характер ядерных сил, трудность решения уравнений движения нуклонов в ядре не позволяют разработать единую теорию атомного ядра. И поэтому в настоящее время прибегают к рассмотрению приближенных моделей ядра. Наиболее известны из них капельная и оболочечная.
1. Капельная модель (Я.И.Френкель, Н.Бор). Эта модель основана на аналогии между поведением нуклонов в ядре и молекул в капельке жидкости. Силы, действующие между молекулами в жидкости (силы поверхностного натяжения) и ядерные силы обладают сходными свойствами (не являются центральными, для них характерно насыщение). Объем капли и ядра зависит от числа частиц. Плотность капли жидкости и плотность ядра остаются величинами постоянными.
В рамках этой модели удалось получить полуэмпирическую формулу для энергии связи ядра и объяснить механизм деления ядер.
2. Оболочечная модель. В данной модели
нуклоны ядра располагаются по оболочкам
(подобно электронам в атоме) с дискретными
значениями энергии. Устойчивость ядра
зависит от степени заполнения оболочек.
Ядра с полностью заполненными оболочками
наиболее устойчивы. Магические числа
– 2, 8, 20, 28, 50, 82, 126. Ядра, содержащие это
число протонов или нейтронов, наиболее
устойчивы (
![]() ).
В рамках этой модели удалось объяснить
устойчивость ядер и периодичность их
свойств.
).
В рамках этой модели удалось объяснить
устойчивость ядер и периодичность их
свойств.
