3.9.4. Волновая функция и ее статистический смысл.

Экспериментальное подтверждение гипотезы де Бройля поставило перед специалистами новые проблемы. В частности необходимо было истолковать физическую природу волн де Бройля.

Для выяснения природы волн де Бройля сравним дифракцию света и частиц. Согласно волновым представлениям о природе света интенсивность дифракционной картины пропорциональна квадрату амплитуды световой волны, но с точки зрения корпускулярной теории – интенсивность картины определяется числом фотонов, попадающих в данную точку дифракционной картины. Следовательно, число фотонов в данной точке определяется квадратом амплитуды световой волны, в то время как для одного фотона квадрат амплитуды световой волны определяет вероятность попадания фотона в ту или иную точку пространства.

Дифракционная картина, наблюдаемая для микрочастиц, также характеризуется неодинаковым распределением потоков частиц. В одних направлениях наблюдается большее количество частиц, в других меньшее. В максимуме дифракционной картины – наибольшее количество частиц и наибольшая интенсивность волн де Бройля. Таким образом, дифракционная картина для микрочастиц является отражением статистической (вероятностной) закономерности, согласно которой частицы попадают в те точки, где интенсивность волн де – Бройля наибольшая.

Необходимость вероятностного подхода к описанию микрочастиц является важнейшей отличительной особенностью квантовой механики.

Волны де Бройля нельзя истолковывать как волны вероятности (вероятность не может быть отрицательной). Поэтому М.Борн предположил, что по волновому закону меняется не сама вероятность, а некая величина названная амплитудой вероятности или пси – функцией, или волновой функцией. Вероятность обнаружить частицу в той или иной точке пространства определяется квадратом волновой функции, т.е.

. 9.5

4.9.4. Уравнение Шредингера.

Необходимость применения статистического метода привело к выводу о том, что уравнение движения в квантовой механике, описывающее движение микрочастиц во внешних силовых полях, должно быть уравнением, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Очевидно, что это уравнение должно быть уравнением относительно волновой функции , так как именно она определяет вероятность обнаружения частицы в объеме в данный момент времени. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением.

Следует отметить, что это уравнение не выводится, а постулируется (подобно второму закону Ньютона или уравнениям Максвелла). В 1926 году Шредингер нашел вид этого уравнения

, 9.6

где - волновая функция, - потенциальная энергия частицы. Это уравнение называется общим уравнением Шредингера.

Для многих физических процессов, происходящих в микромире это уравнение можно упростить, исключив из него зависимость от времени . Это возможно в том случае, если силовое поле стационарно, т.е. функция не зависит явно от времени и имеет смысл потенциальной энергии . В этом случае уравнение Шредингера будет иметь вид

9.7

и называется уравнением Шредингера для стационарных состояний. В это уравнение в качестве параметра входит полная энергия частицы Е. В теории дифференциальных уравнений доказывается, что это уравнение имеет решение лишь при определенных значениях параметра Е, которые получили название собственных значений энергии. Собственные значения энергии могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном спектре, во втором – о дискретном. В качестве примера рассмотрим движение свободной частицы.

При движении свободной частицы ее потенциальная энергия равна нулю и полная энергия совпадает с кинетической энергией. Для свободной частицы, движущейся вдоль оси Х, уравнение Шредингера будет иметь вид:

.

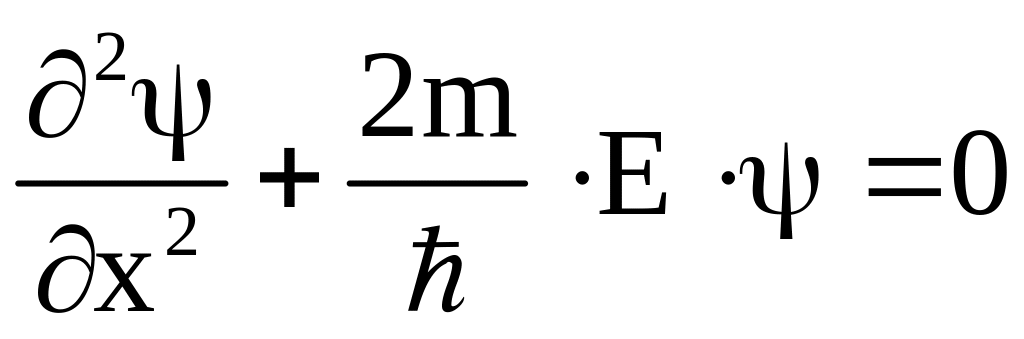Прямой подстановкой можно убедиться в том, что частным решением этого уравнения является функция

,

где и . Так как и, учитывая, что длина волны де Бройля , то будем иметь . Следовательно, - из полученного выражения следует, что зависимость энергии от импульса оказывается обычной для нерелятивистской частицы и для ее энергии получается выражение . Из этого выражения следует, что энергия свободной частицы может принимать произвольные значения.