2.1.4. Преломление света на сферической поверхности.
Рассмотрим преломление света на
сферической поверхности. Пусть две
прозрачные среды с показателями
преломления
разделены сферической поверхностью
радиуса R (рис. 5).
Для построения изображения точки проведем луч, идущий вдоль главной оптической оси и луч, идущий под малым углом к оптической оси. Будем рассматривать только лучи, составляющие с оптической осью столь малые углы, что для них синусы и тангенсы можно заменять самими углами, а косинусы считать равными единице.
Р
ассмотрим
луч SA, исходящий из точки
S, падающий на границу
раздела сред в точке А и пересекающий
после преломления главную оптическую
ось в точке
.
При соблюдении указанного правила
знаков закон преломления света можно
записать в виде:
.
1.5
Заменив синусы углов самими углами, будем иметь:
.
1.6
Из треугольников
будем
иметь
и
.
Подставляя в 1.6, получим:
.
1.7
Из треугольников
с учетом малости углов можно найти
.
1.8
Подставляя эти значения в 1.7, после преобразования получим:
.
1.9
Формула 1.9 позволяет определить положение изображения точки, зная положение точки и радиус кривизны поверхности.
3.1.4. Тонкие линзы. Формула тонкой линзы.
Случай преломления света на одной сферической поверхности сравнительно редок. Большинство реальных систем содержит, по крайней мере, две преломляющих поверхности или больше двух.
Система сферических поверхностей называется центрированной, если центры всех поверхностей лежат на одной прямой, которая называется главной оптической осью.
На практике большое значение имеет простейший случай центрированной системы, состоящей всего из двух сферических поверхностей, ограничивающих какой-либо прозрачный хорошо преломляющий материал от окружающего воздуха. Такая система получила название линзы.
Л
инза
называется тонкой, если ее вершины можно
считать совпадающими, т.е. если толщина
линзы мала по сравнению с радиусами
кривизны ограничивающих поверхностей
(рис. 6). В дальнейших расчетах мы будем
считать, что точки
и
сливаются в одну точку О. Все расстояния
будем отсчитывать от этой точки. Точка
О получила название оптического центра
линзы.
Преломление на первой сферической
поверхности создало бы без второй
преломляющей поверхности в сплошном
стекле с показателем преломления
,
изображение на расстоянии
от оптического центра, так что,
.
1.10
Для второй сферической поверхности
точка С является мнимым источником
света. Построение изображения этой
точки на второй преломляющей поверхности
дает точку
на
расстоянии
от оптического центра, так что
.
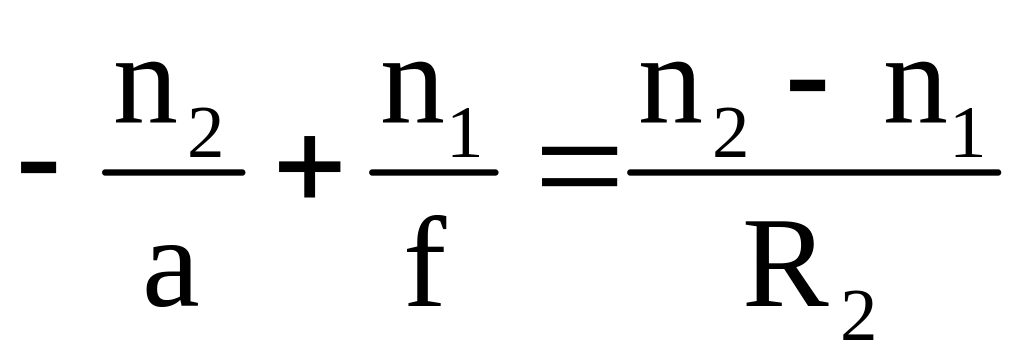1.11
Суммируя выражения 1.10 и 1.11 получим:
1.12
Вводя относительный показатель
преломления
,
окончательно получим общую формулу
линзы:
1.13
Общая формула линзы пригодна для любой линзы при произвольном положении источника света. Нужно только принять во внимание знаки d, f, R. Расстояние от предмета до линзы d считаем положительным для действительного источника (на линзу падает расходящийся пучок лучей). Для мнимого источника это расстояние считается отрицательным (на линзу падает сходящийся пучок лучей). Расстояние от линзы до изображения f считается положительным для действительного изображения источника света и отрицательным - для мнимого изображения. Для выпуклой поверхности радиус кривизны считается положительным, для вогнутой поверхности – отрицательным.
Если
светящаяся точка, лежащая на главной
оптической оси, удаляется от линзы, то
изображение ее перемещается. Положение
изображения, когда источник удален в
бесконечность, носит название фокуса
линзы. Другими словами, это есть точка,
в которой пересекаются лучи (или их
продолжения) падающие на линзу параллельно
главной оптической оси (рис. 7). Расстояние
от линзы до фокуса называется фокусным
расстоянием F. Для
определения фокусного расстояния линзы
мы имеем:
при
1.14
Из выражения 1.14 следует, что фокусное расстояние линзы зависит только от относительного показателя преломления материала линзы и радиусов кривизны ограничивающих поверхностей.
Вводя фокусное расстояние линзы F выражение 1.14, может быть записано в виде:
1.15
Величина
называется оптической силой линзы.
Единица измерения
диоптрия.
Линзы с положительной оптической силой называются собирающими, а с отрицательной – рассеивающими.
Построение изображения предмета в линзах осуществляется с помощью следующих лучей:
луча, проходящего через оптический центр линзы и не меняющего своего направления распространения;
луча, идущего параллельно главной оптической оси; после преломления в линзе луч (или его продолжение) проходят через фокус;
луча (или его продолжения), идущего через фокус линзы; после преломления в линзе он идет параллельно главной оптической оси.
Д
ля
примера на рисунке 8 приведено построение
изображения в собирающей и рассеивающей
линзах.
Отношение линейных размеров изображения и предмета называется линейным увеличением.
.
1.16