3.8.4. Рентгеновское излучение.

В 1895 году В.Рентгеном было открыто излучение, получившее название рентгеновского. Оно представляет собой электромагнитное излучение с длиной волны порядка . Источником рентгеновского излучения является рентгеновская трубка, в которой ускоренные до больших значений энергии электроны, бомбардируют анод (металлическая мишень из тяжелых металлов), испытывая на нем резкое торможение.

Исследование спектрального состава рентгеновского излучения показало, что его спектр имеет сложную структуру. Он представляет собой наложение сплошного спектра, ограниченного со стороны коротких волн некоторой границей и линейчатого спектра – совокупности отдельных очень резких линий, появляющихся на фоне сплошного спектра. Характер сплошного спектра совершенно не зависит от материала анода, а определяется только энергией электронов, бомбардирующих анод. Исследования показали, что оно испускается электронами в результате их торможения при столкновении с анодом и поэтому, сплошной рентгеновский спектр получил название тормозного спектра. Наличие коротковолновой границы спектра подтверждает справедливость квантовой теории. Предельная энергия рентгеновского кванта соответствует тому случаю, когда вся кинетическая энергия электрона переходит в энергию кванта, т.е.

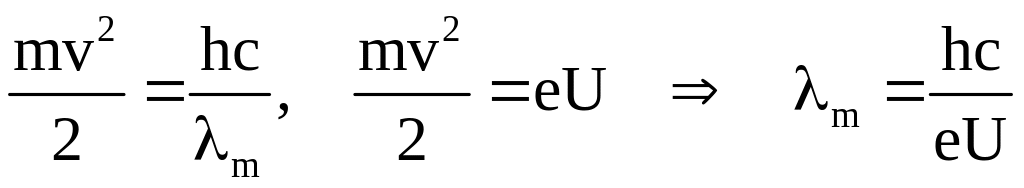. 8.8

Измеряя границу рентгеновского спектра по данной формуле можно вычислить значение постоянной Планка .

При увеличении кинетической энергии электронов (увеличение напряжения на электродах трубки) наряду со сплошным возникает линейчатый спектр, зависящий от материала анода и называемый характеристическим спектром.

П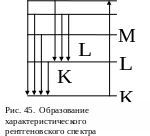 о сравнению с оптическими спектрами химических элементов (они самые разнообразные) рентгеновские спектры совершенно однотипны и состоят из нескольких серий, обозначаемых . Каждая серия состоит из нескольких линий. При переходе от легких элементов к тяжелым структура спектра не меняется, лишь весь спектр смещается в сторону более коротких волн. Особенность этих спектров состоит в том, что атомы каждого элемента, независимо от того свободны они или входят в состав химического соединения обладают определенным характерным для данного элемента линейчатым спектром.

Изучение структуры характеристических рентгеновских спектров приводит нас к выводу о том, что их возникновение связано с процессами, происходящими во внутренних заполненных электронных оболочках атомов, которые имею сходное строение.

Под действием кого-нибудь внешнего фактора электрон с оболочки К может перейти на более высокую оболочку, а в К-оболочке возникает вакансия, куда может перейти электрон с другой оболочки, излучая при этом рентгеновский квант.

Мозли установил, что частоту линий в характеристическом рентгеновском спектре можно определить по формуле, аналогичной сериальной формуле для атома водорода

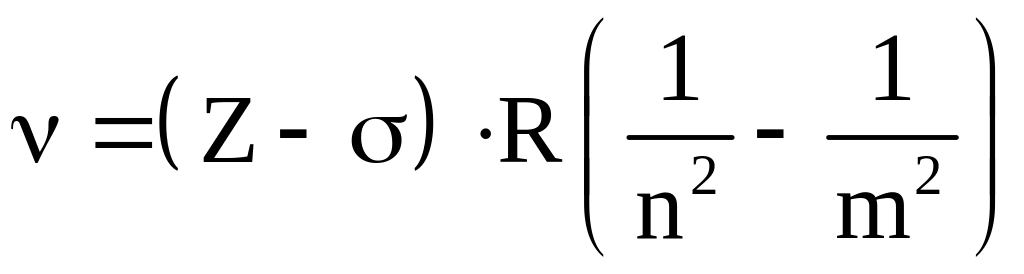, 8.9

где - порядковый номер элемента в таблице Менделеева, - постоянная экранирования.