3.6.4. Законы Стефана – Больцмана и смещения Вина.

Закон Кирхгофа ставит в центре внимания теории теплового излучения универсальную функцию Кирхгофа и поэтому нахождение ее явной зависимости от частоты и температуры являлось важнейшей задачей.

Решение этой задачи было найдено не сразу. В начале был установлен теоретически и экспериментально подтвержден закон, определяющий суммарное излучение абсолютно черного тела, т.е. его энергетическую светимость закон Стефана - Больцмана. Опираясь на законы термодинамики и идею о существовании давления излучения, пропорционального его плотности, Стефан и Больцман показали, что энергетическая светимость абсолютно черного тела пропорциональна четвертой степени абсолютной температуры, т.е.

, 6.6

где - постоянная Стефана – Больцмана. Экспериментальные исследования Луммера и Вина (1895 г.) и Луммера и Прингсгейма (1897 г.) подтвердили этот вывод.

Вин, опираясь на законы термодинамики и электродинамики, показал, что максимум функции приходится на длину волны, определяемую из закона

, 6.7

где - постоянная Вина, а закон получил название закона смещения Вина.

Кроме того, Вин показал, что в максимуме спектральная плотность излучательности абсолютно черного тела пропорциональна пятой степени абсолютной температуры.

4.6.4. Формулы Релея – Джинса, Вина и Планка

Если теоретически осуществить черное тело как совокупность бесконечного числа гармонических осцилляторов, каждый из которых дает отдельную монохроматическую линию, а все вместе сплошное излучение, то, пользуясь законами, управляющими поведением таких осцилляторов, можно прийти к законам теплового излучения абсолютно черного тела.

Идя по этому пути, Релей и Джинс получили для универсальной функции Кирхгофа выражение

6.8

формула Релея – Джинса.

Как показал опыт, это выражение хорошо согласуется с опытными данными только в области малых частот и резко расходится с ними в области высоких частот. Кроме того, попытка получить закон Стефана – Больцмана на основе этой формулы приводит к абсурдному результату. В самом деле,

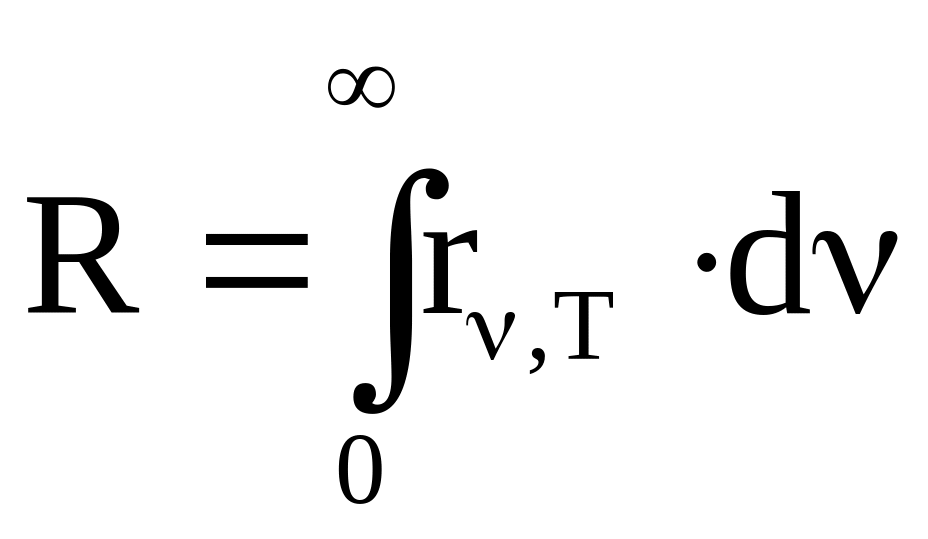6.9

и, следовательно, по Релею – Джинсу

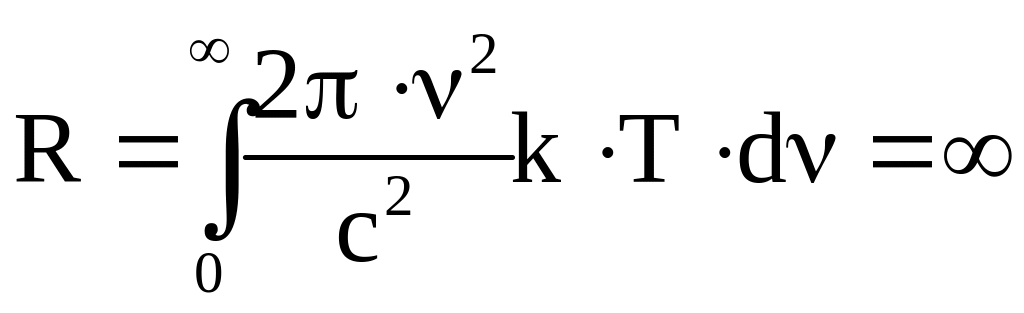. 6.10

В то время как по закону Стефана – Больцмана энергетическая светимость абсолютно черного тела имеет конечное значение . Этот вывод получил название «ультрафиолетовой катастрофы».

В 1896 году Вин для универсальной функции Кирхгофа получил выражение

. 6.11

Эта формула хорошо согласуется с опытом в области высоких частот и резко расходится в области низких.

Таким образом, в рамках классической физики получить выражение для универсальной функции Кирхгофа не удалось.

М.Планк, анализируя положение, пришел к выводу о том, что причина неудач лежит в неправильности приложения законов классической физики к атомным осцилляторам. По классическим законам энергия осциллятора может принимать любые значения, так как энергия пропорциональна квадрату амплитуды колебания. В соответствии с этим осциллятор может излучать любое количество энергии. По мнению М.Планка эти законы не применимы к атомным осцилляторам.

Планк предположил, что атомный осциллятор может иметь энергию пропорциональную частоте колебаний, т.е. , где - постоянная Планка. В соответствии с этим и излучение энергии может происходить только порциями, пропорциональными . Учитывая новые законы, Планк для универсальной функции Кирхгофа получил выражение

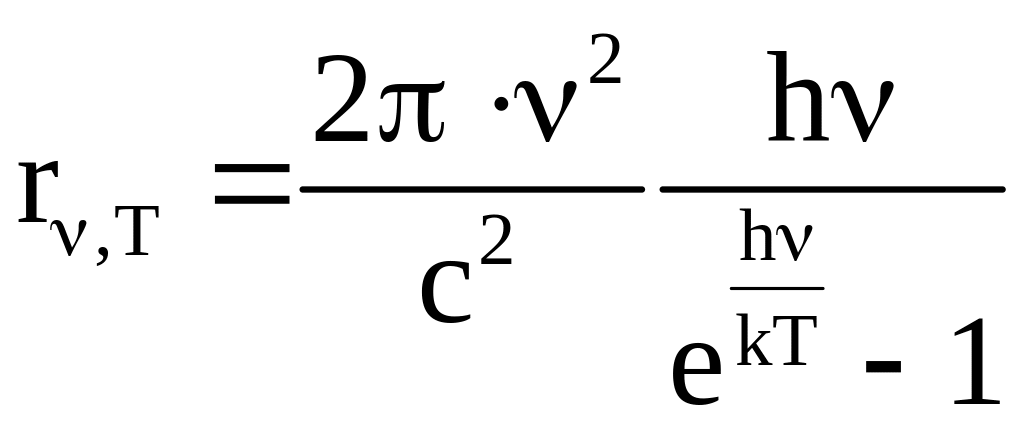. 6.12

В декабре 1900 года на заседании немецкого физического общества Курльбаум и Прингсгейм докладывали о новых измерениях спектральной плотности излучательности абсолютно черного тела и посетовали на то, что ни одна из существующих теорий не может дать правильный результат. Тогда Планк предложил провести расчеты по выведенной им формуле. Полученное выражение дает полное совпадение с самыми тщательными экспериментальными данными и, следовательно, является полным решением задачи, поставленной Кирхгофом.

Найдя эту формулу, Планк, чтобы объяснить ее должен был приписать физический смысл двум константам, которые в ней появились. Для первой константы это было легко. Но что касается второй, которую Планк назвал «элементарным квантом действия», то это «… либо фиктивная величина, и тогда весь вывод закона излучения был в принципе ложным и представлял собой всего лишь пустую игру в формулы, лишенную смысла, либо же вывод закона излучения опирается на некую физическую реальность, и тогда квант действия должен приобрести фундаментальное значение в физике и означает собой нечто совершенно новое и неслыханное, что должно произвести переворот в нашем физическом мышлении, основывавшемся со времен Лейбница и Ньютона, открывшим дифференциальное исчисление, на гипотезе непрерывности всех причинных соотношений.»

При низких частотах и поэтому и формула Планка переходит в формулу Релея – Джинса.

Легко убедиться в том, что, используя формулу Планка можно получить и другие законы теплового излучения. При этом оказывается, что постоянные Стефана – Больцмана и Вина можно выразить через постоянные

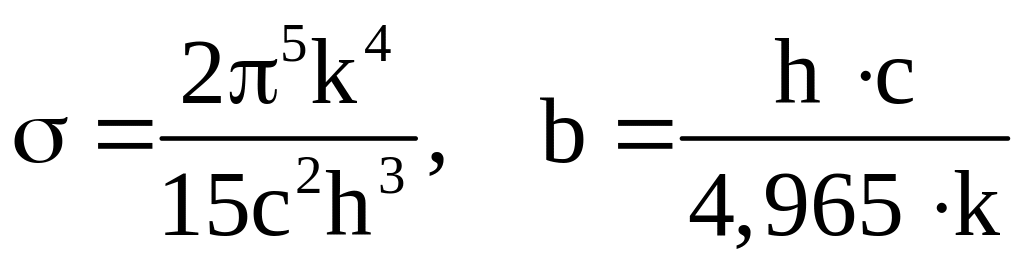
и сравнив теоретические и практические значения можно было делать вывод о справедливости данной теории. Расчеты показали полное совпадение практических и теоретических значений . По известным значениям можно было найти значение постоянной Планка .

Это интересно. С математической точки зрения, задача, поставленная Планком, была достаточно простой. Необходимо было интеграл из расходящегося сделать сходящимся. Иначе обстояло дело с физическим смыслом введенной величины.