3.5.4. Следствия из преобразований Лоренца.

Из преобразований Лоренца вытекает ряд следствий.

1. Относительность одновременности.

Пусть в системе К в точках с координатами и происходят два события в моменты времени и . В системе им соответствуют координаты и , моменты времени и .

Если события происходят в одной точке и являются одновременными , то в соответствии с преобразованиями Лоренца и , т.е. эти события будут одновременными и системе .

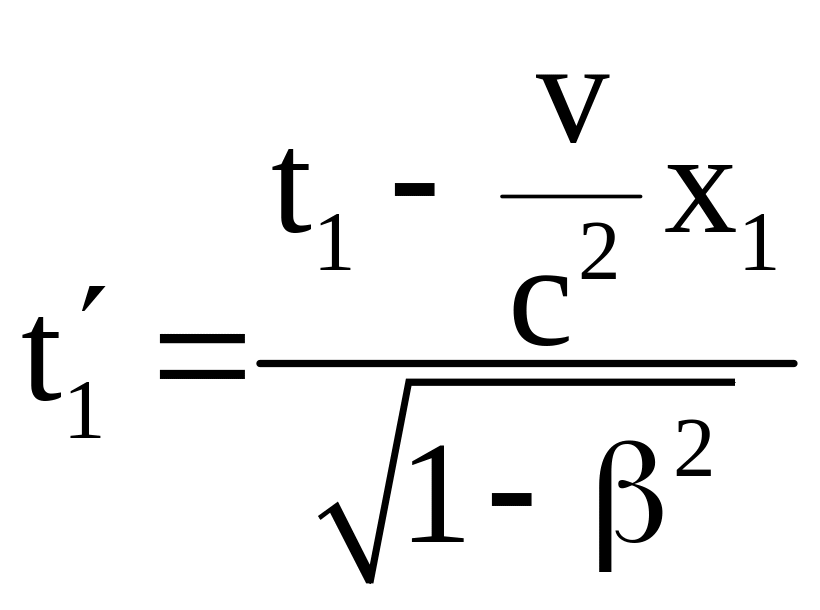Если же эти события в системе К пространственно разделены , но одновременны ( ), то в системе им будут соответствовать моменты времени и , и это означает, что . Другими словами одновременность пространственно разделенных событий относительна.

2. Относительность промежутков времени.

Пусть в некоторой точке системы К, происходит событие, длительность которого . Длительность этого же события в системе будет равна . Но согласно преобразованиям Лоренц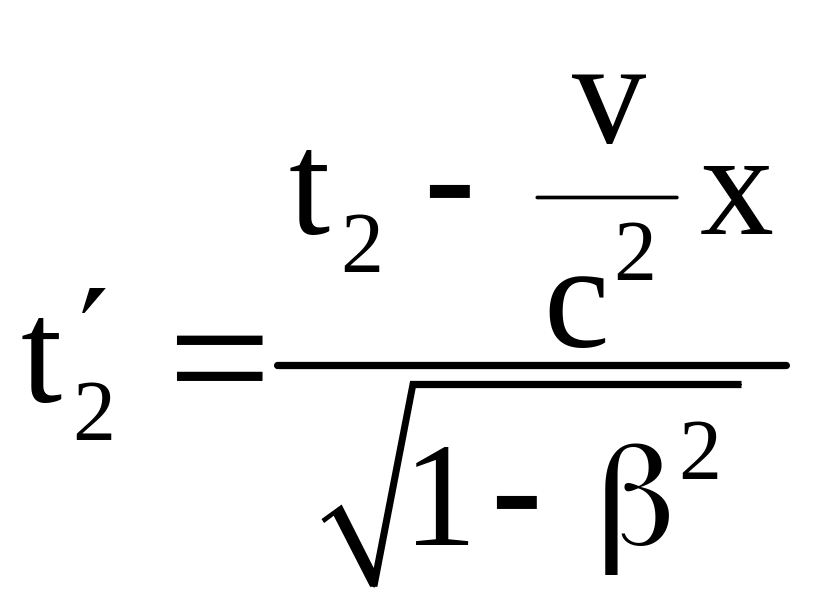а , и тогда

. 5.2

Из полученного выражения следует, что длительность события наименьшая в системе отсчета, относительно которой, оно покоится. Другими словами часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов.

3. Относительность длин отрезков.

Пусть стержень, покоящийся относительно системы имеет длину . Тогда длина этого стержня в системе будет равна . Согласно преобразованиям Лоренца .

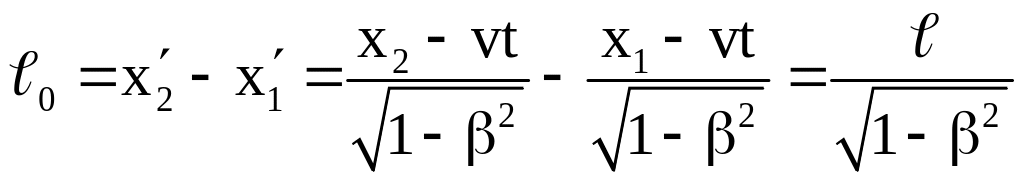Отсюда

, 5.3

т.е. длина стержня, измеренная в системе относительно которой он движется, оказывается меньше длины покоящегося стержня.

4. Релятивистский закон сложения скоростей.

Относительность промежутков времени и длин отрезков ведет к радикальному пересмотру всей кинематики. Прежде всего, это касается классического закона сложения скоростей, так как согласно второму постулату Эйнштейна движение со скоростью большей скорости света в вакууме невозможно.

Если в системе движение в каждый момент времени задается координатами , то в системе в моменты времени координатами , то

.

Дифференцируя два последних равенства можно найти, что и тогда после несложных математических преобразований получим

. 5.4

Мы получили закон сложения скоростей в релятивисткой механике. Очевидно, что при он переходит в классический закон сложения скоростей. Из полученного выражения следует, что даже в том случае, если , .

5. Интервал между событиями.

Все сказанное выше говорит о том, что теория относительности представляет собой стройную систему, которая не только устраняет кажущиеся противоречия между отдельными экспериментальными фактами, но и приводит к пересмотру наших представлений о пространстве и времени.

В классической механике (механике Ньютона) абсолютное пространство и абсолютное время никак не связаны между собой. Относительный характер промежутков времени и длин отрезков означает, лишь относительность отдельных компонент некоторой реальной величины, которая как целое имеет вполне определенный реальный физический смысл, не зависящий от выбора системы отсчета, т.е. являющейся инвариантной по отношению к преобразованиям Лоренца. По мнению Эйнштейна в четырехмерном пространстве, в котором каждое событие характеризуется четырьмя координатами , такой величиной является интервал между событиями

, 5.5

где .

Можно показать, что при переходе от одной системы отсчета к другой интервал между событиями не изменяется.

4.5.4. Зависимость массы от скорости. Взаимосвязь массы и энергии.

Второй закон Ньютона инвариантный относительно преобразований Галилея становится не инвариантным относительно преобразований Лоренца. Эйнштейн показал, что второй закон Ньютона будет инвариантен относительно преобразований Лоренца, если импульс тела будет определяться по формуле

. 5.6

Это говорит о том, что масса тела зависит от скорости движения

. 5.7

Преобразование этого выражения приводит нас к следующему выводу

.

Это выражение можно записать в виде

. 5.8

Мы получили выражение фундаментального закона природы - взаимосвязи массы и энергии - . - энергия покоя. И тогда .

Преобразование выражения 5.7 приводит нас еще к одному выводу:

Так как 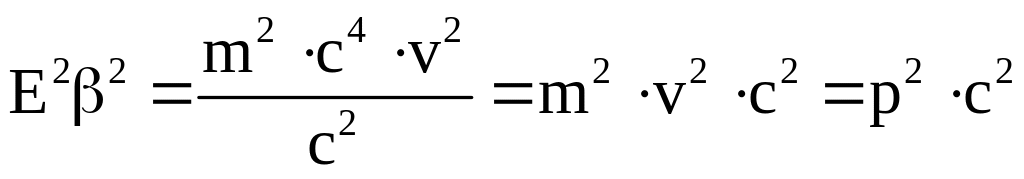. Тогда

. 5.9

Мы получили закон сохранения энергии-импульса.