Выполнение работы

1. Записать данные лабораторной установки и атмосферное давление.

2. Открыть кран и определить время в течение которого из сосуда вытекает объем жидкости равный 100 – 200 мл.

3. По формулам /2/, /3/, /6/ вычислить коэффициент динамической вязкости, плотность воздуха и среднюю арифметическую скорость движения молекул воздуха.

4. По формулам /7/, /10/ определить среднюю длину свободного пробега и эффективный диаметр молекулы воздуха.

5. Опыт повторить не менее трех раз при других значениях объема жидкости, вытекающей из сосуда.

6. Результаты измерений и расчетов занести в таблицу.

Таблица 13.1.

№№	V	T K	р Па	Па	с	м	м

7. Определить среднее значение эффективного диаметра и средней длины свободного пробега молекулы воздуха.

Контрольные вопросы.

1. Что называется эффективным диаметром молекулы?

2. Что такое средняя длина свободного пробега молекулы?

3. Напишите уравнение Менделеева-Клапейрона.

4. Как записывается формула Пуазейля?

5. Объясните явления переноса в газах.

Работа № 14 поперечные колебания струны

Цель работы: определение собственных частот колебаний струны с закрепленными концами.

Оборудование: струна с закрепленными концами, звуковой генератор, набор грузов.

Теоретическое введение

Объектом исследования в данной лабораторной работе является стальная струна, натянутая между двумя точками ее закрепления. Составим уравнение колебаний струны. Для простоты рассуждений будем рассматривать малые колебания струны, такие, что ее длину можно считать постоянной.

В озьмем малый элемент струны, которому соответствует отрезок на оси «Х» (рис. 14.1). Мгновенный профиль струны зададим функцией , определяющей отклонение ее элементов от положения равновесия.

Найдем вертикальную составляющую силы F, действующей на выделенный элемент струны. Очевидно, что

. /1/

Так как мы рассматриваем малые колебания,

/2/

и тогда

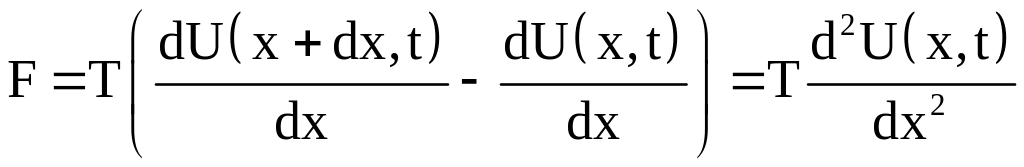. /3/

Запишем второй закон Ньютона для элемента струны

, /4/

где dm – масса элемента струны.

Так как , а , то

. /5/

Полученное уравнение можно преобразовать к виду

, /6/

где .

Покажем, что полученное уравнение описывает стоячие колебания струны. Для этого его решение запишем в виде

. /7/

Подстановка этого решения в уравнение /6/ приводит к следующему уравнению

. /8/

Решение уравнения /8/ ищется в виде

, /9/

где А, В – постоянные интегрирования.

Так как струна закреплена в точках , то это значит, что

. /10/

Из первого условия /10/ следует, что ; второе условие приводит к соотношению

, /11/

которое имеет решения при

, /12/

где .

Отсюда можно найти

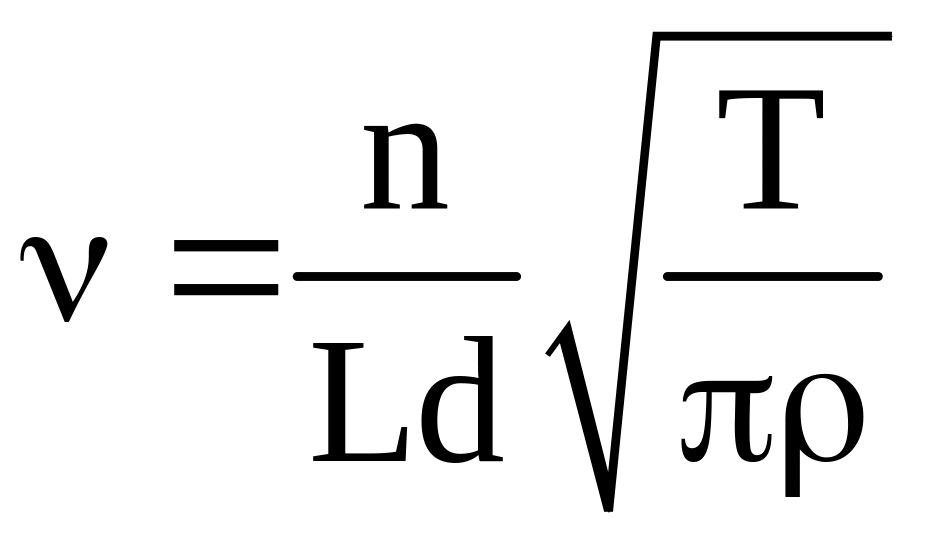. /13/

Это уравнение определяет частоты собственных колебаний струны с закрепленными концами. Частота соответствующая называется основным тоном, а остальные - обертонами.