Федеральное государственное образовательное бюджетное учреждение
высшего профессионального образования
«Финансовый университет при Правительстве Российской Федерации»
КАФЕДРА ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
ЛАБОРАТОРНАЯ РАБОТА
ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
Обработка результатов наблюдения
Вариант: __14_____________________________
Группа: ___Н-2-1__________________________
Выполнил: _Бицадзе Бачуки________________
Проверил: ____Рябов П.Е.__________________
Оценка: _________________________________
Подпись: ________________________________
Дата: ___________________________________
Москва 2013
Оглавление
Используемые формулы: 2
Постановка задачи 6
Используемые данные 7
Вычисления и представление результатов 7
Однофакторный дисперсионный анализ 18
Двухфакторный дисперсионный анализ 24
Выводы: 30
Используемые формулы:
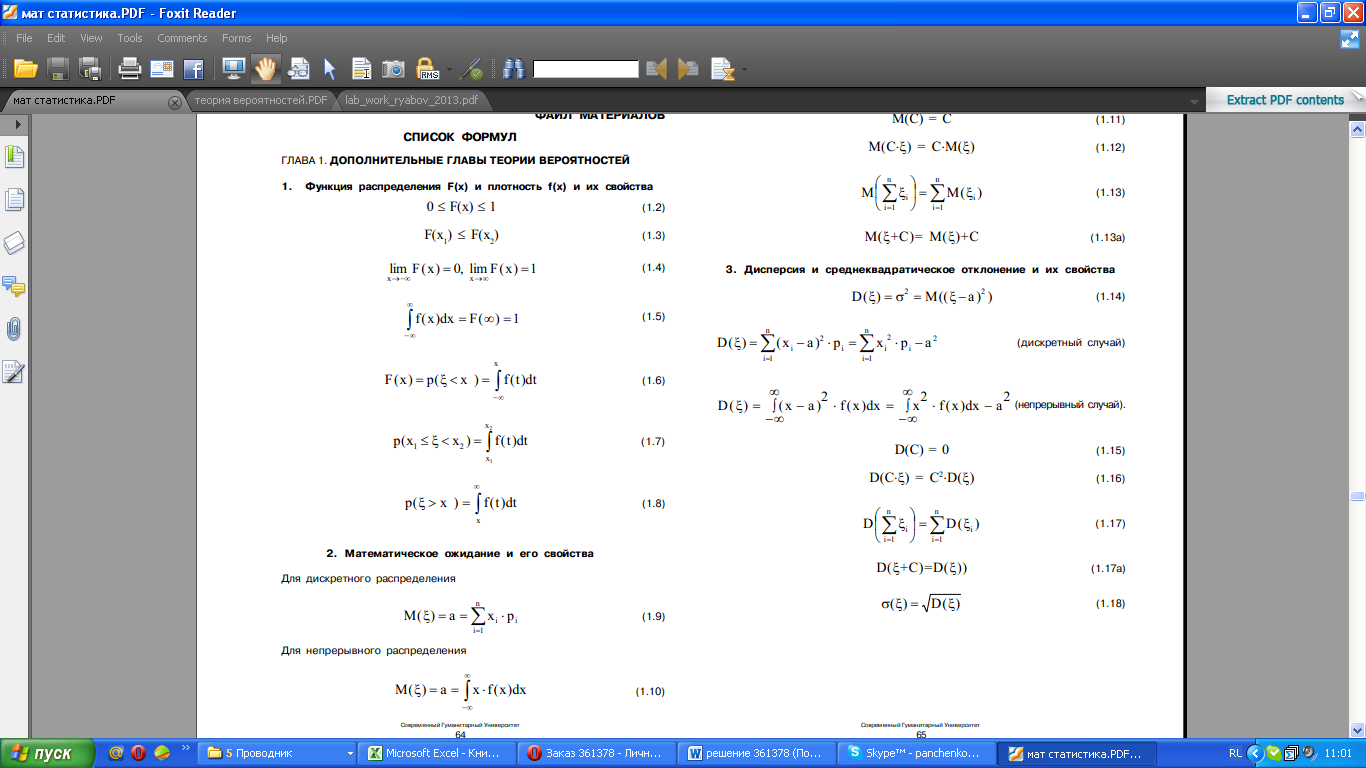
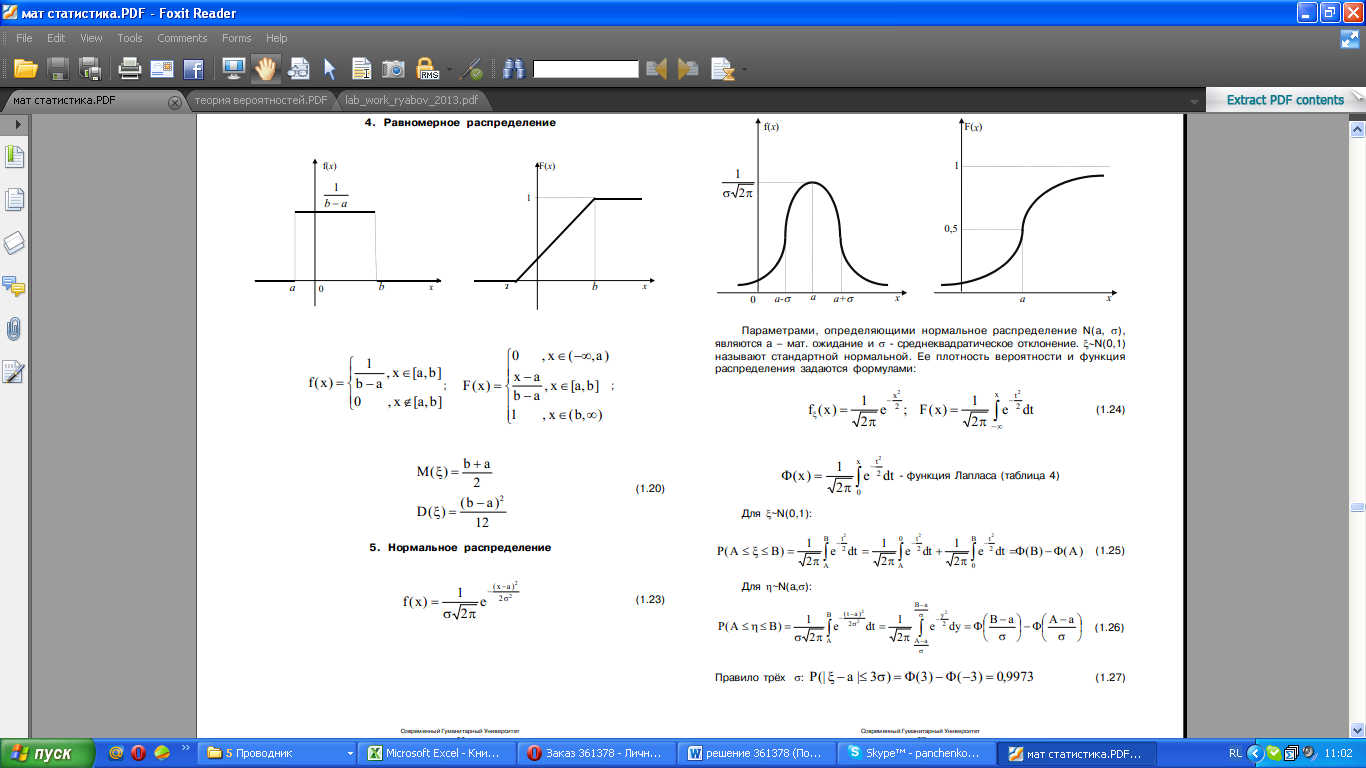
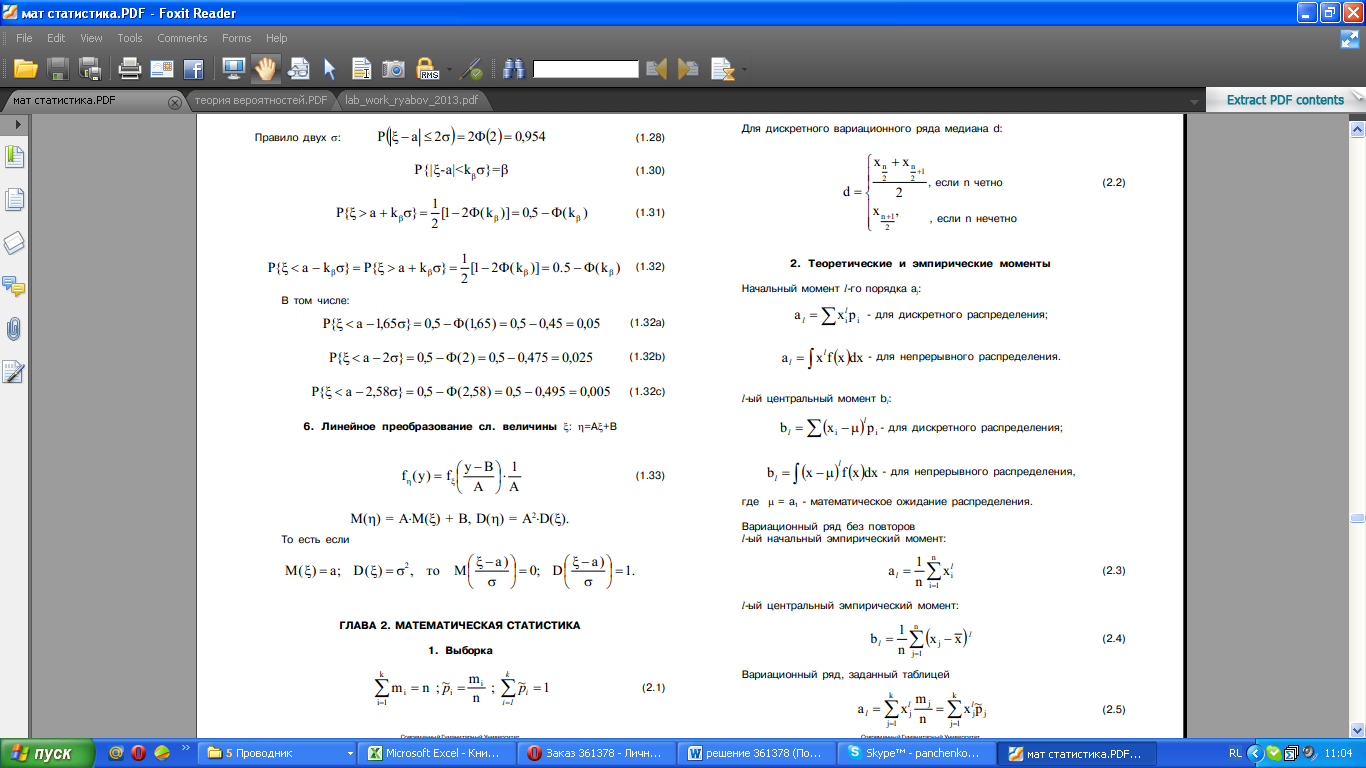
Тема 1 Постановка задачи
Задача. Служба маркетинга оценивает дилеров фирмы по объему продаж. Сведения об объеме ежедневных продаж товара (в тыс. ден. ед.) некоторым дилером за последние 100 дней приведены ниже. Требуется:
Построить интервальный вариационный ряд; полигон и гистограмму (на одном рисунке); кумуляту (на другом рисунке).
Вычислить выборочные характеристики: среднее, дисперсию, среднее квадратичное отклонение, коэффициент вариации, асимметрию, эксцесс, моду, медиану.
Заменив параметры нормального закона распределения их выборочными характеристиками, скорректированными на поправку Шеппарда, рассчитать и построить графики функции плотности и функции распределения нормального закона, «наложив» эти графики соответственно на полигон и кумуляту.
На 5%-ном уровне значимости проверить гипотезу о нормальном законе распределения объема ежедневных продаж.
Предположив нормальность распределения объема продаж, построить 95%-ные интервальные оценки математического ожидания, дисперсии и среднего квадратичного отклонения.
Предположив нормальность распределения объема продаж, на 5%-ном уровне значимости проверить следующие гипотезы:
а) 
при альтернативной гипотезе
(здесь
[s] — целая часть числа s); рассчитать
вероятность ошибки второго рода,
задавшись альтернативным числовым
значением M(X);
б) 
при альтернативной гипотезе
;
рассчитать вероятность ошибки второго
рода, задавшись альтернативным числовым
значением D(X).
Используемые данные
9,6 |
11,35 |
13,33 |
11,48 |
13,1 |
12,49 |
20,63 |
19,31 |
14,77 |
13,68 |
19,25 |
9,11 |
19,1 |
18,65 |
16,61 |
12,37 |
13,87 |
16,14 |
20,69 |
18,43 |
18,23 |
9,52 |
15,98 |
14,5 |
15,38 |
13,71 |
17,21 |
14,48 |
9,15 |
13,6 |
14,73 |
12,41 |
17,46 |
11,41 |
13,01 |
20,1 |
10,84 |
11,36 |
11,71 |
13,03 |
7,28 |
18,56 |
14,3 |
17,53 |
7,58 |
18,48 |
17,35 |
12,59 |
8,15 |
12,35 |
14,18 |
7,72 |
18,68 |
16,44 |
8,05 |
16,69 |
15,15 |
17,07 |
14,31 |
12,9 |
10,54 |
13,53 |
13,53 |
12,44 |
3,51 |
12,55 |
16,86 |
14,02 |
9,1 |
12,43 |
17,18 |
13,76 |
0,97 |
13,58 |
16,93 |
7,41 |
13,06 |
14,85 |
19,14 |
14,16 |
13,92 |
21,13 |
25,26 |
10,93 |
4,81 |
24,61 |
10,29 |
12,62 |
14,27 |
13,64 |
13,05 |
18,29 |
14,33 |
14,97 |
11,62 |
13,13 |
12,48 |
7,85 |
9,97 |
9,83 |