Практическое занятие №5 Изучение термодинамического процесса

Цель работы: изучить термодинамические газовые процессы

Справочный материал

При исследовании термодинамических процессов используются уравнение состояния идеальных газов и математическое выраже­ние первого закона термодинамики. В общем случае любые два термодинамических параметра из трех могут изменяться произвольно. Термодинамика изучает пять основных процессов идеальных газов:

1.изохорный, (v= const) происходящий при постоянном объеме газа; 2.изобарный, (р = const) происходящий при постоянном давлении; 3.изотермический, (Т = const) происходящий при постоянной темпера­туре; 4.адиабатный, (q = 0) протекающий без подвода или отвода теплоты, т.е. протекающий без теплообмена с окружающей средой;

5.политропный — обобщенный процесс изменения всех параметров рабочего тела при наличии теплообмена; для него четыре предыдущих процесса являются частными случаями.

Для изучения этих процессов необходимо определить:

уравнение процесса, которое устанавливает закономерность изменения состояния рабочего тела; графическое изображение процесса в диаграммах; связь между параметрами в процессе; изменение внутренней энергии рабочего тела в процессе; работу, совершаемую рабочим телом в процессе; теплоту, участвующую в процессе.

Изохорный процесс Такой процесс может совершаться рабочим телом, находящимся в цилиндре при неподвижном поршне, если к рабочему телу подводится теплота от источника теплоты (см. рис.1) или отводится теплота от рабочего тела к холодильнику. При изохорном процессе выполняется условие dv=0 или v=const. Уравнение изохорного процесса получим из уравнения состояния идеального газа при v=const. Уравнение изохорного процесса: v = const.

Г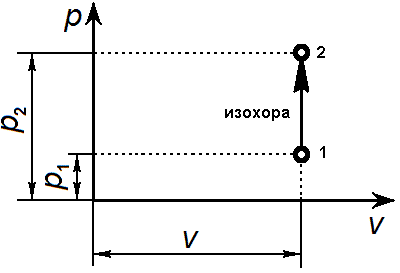 рафически в p-v-диаграмме изохорный процесс изо­бражается линией, параллельной оси давлений Линии изохорного процесса в диаграмме состояния называется изохорой.

Связь между параметрами в изохорном процессе подчиняется  закону Шарля

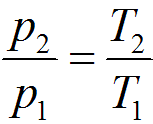
И изохорном процессе вся подведенная теплота расходуется на изменение внутренней энергии тела. Для тела с произвольной массой вещества m имеем:

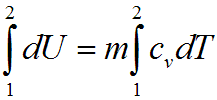
где cv — средняя массовая изохорная теплоемкость в интервале температур от T1, до Т2.

Теплоемкостью называется количество теплоты, которое следует подвести к единице количества вещества для нагревания его на 1 градус. Массовая теплоемкость выражается в кДж/(кг • К), объемная — в кДж/(м3 • К), мольная — в кДж/(кмоль • К).

Так как в изохорном процессе нет изменения объема, то и работа по его изменению не совершается: W1-2 = 0.

Количество теплоты, подведенное в изохорном процессе, равно изменению внутренней энергии. Для произвольной массы вещества:

Изобарный процесс. Уравнение изобарного процесса р= const.

Графически изобарный процесс в р—v-диаграмме изображается прямой линией, параллельной оси объемов. Линия изобарного процесса называется изобарой.

С вязь между параметрами в изобарным процессе выража ется законом Гей-Люссака:

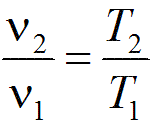
Изменение внутренней энергии газа рассчитывается по формуле:

В изобарном процессе происходит изменение объема рабочего тела, следовательно, совершается работа, определяемая:

Для  произвольной массы газа m формула работы примет:

где V1, V2  - объем m кг газа в начале и конце процесса, м3. Воспользовавшись первым законом термодинамики, мо­жем рассчитать теплоту процесса (для 1 кг газа) по формуле:

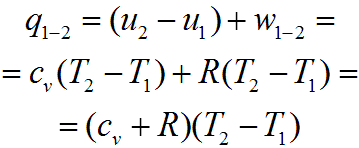
При этом в термодинамике существует связь между изохорной cv и изобарной ср теплоемкостями. Связь устанавливается уравнением Майера:

Тогда выражение для определения количества теплоты для 1 кг газа примет вид:

для произвольной массы газа:

Таким образом, в изобарном процессе теплота расходуется на совершение работы и на изменение внутренней энергии рабоче­го тела.

Изотермический процесс. Уравнение изотермического процесса: Т= const или pv = const.Графически изотермический процесс в р—v-диаграмме изображается в виде равнобокой гиперболы что вытекает из уравнения pv = const, и называется изотермой.

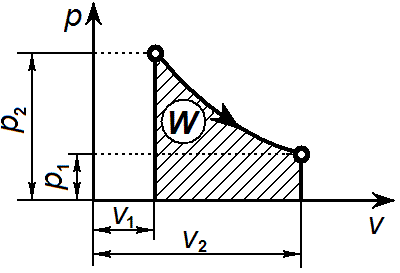Связь между параметрами изотермического процесса определяется законом Бойля — Мариотта:

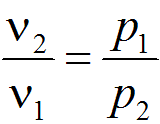
Так как Т1 = Т2, изменение внутренней энергии газа в изотермическом процессе равно нулю:

Совершенная 1 кг газа работа в изотермическом процессе, c  учетом того что RT = const, определяется следующим образом:

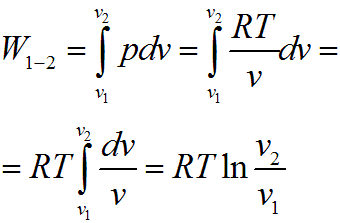
Пользуясь законом Бойля — Мариотта, получим:

Для произвольной массы рабочего тела уравнение работы примет вид:

Графически в p-v диаграмме работа в процессе 1-2 определяется площадью под изотермой. Теплота, участвующая в изотермическом процессе, определится соотношением:

Это означает что вся подведенная в изотермическом процес­се теплота  расходуется на совершение работы.

Адиабатный процесс. Уравнение адиабатного процесса имеет вид:

где k =cp/cv   -показатель адиабаты для идеального газа.

Графически адиабатный процесс на p-v-диаграмме изо­бражается неравнобокой гиперболой, называемой адиабатой. Адиабата круче изотермы, так как к > 1.

С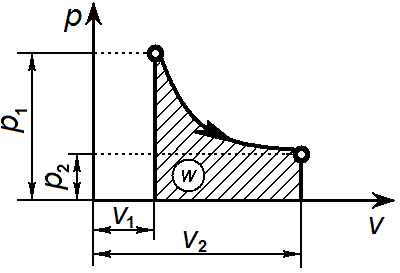 вязь между параметрами процесса определяется, используя уравнение адиабаты и уравнение состояния газа pv = RT:

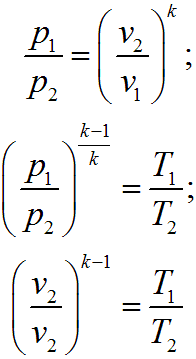
Изменение внутренней энергии для т кг вещества определяется по формуле:

Работа в адиабатном процессе, совершенная 1 кг газа, может быть определена из уравнения первого закона термодинамики :

Так как в адиабатном процессе q=0, то:

и

то есть работа расширения в адиабатном процессе совершается за счет уменьшения внутренней энергии газа.

Адиабатный процесс протекает без подвода теплоты, следовательно  Q=0.

Политропный процесс Уравнение политропного процесса имеет вид

где  n - показатель политропы, который изменяется для разных процессов от 0 до + бесконечности. Рассмотренные ранее процессы являются частными случая­ми иолитроппых процессов:

е сли n = к, то pvk = const — адиабатный процесс; если n = 1, то pv = const — изотермический процесс; если n = 0, то pv0 = p = const — изобарный процесс; если n  ± ?, то представив pvn = const как рn v = const, имеем v=const — изохорный процесс. Показатель изотропы n можно определить, если известны два состояния политропном процесс

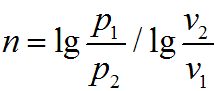
Графическое изображение политропного процесса в р—v-диаграмме имеет вид кривой, которая называется политропой. Соотношение параметров данного процесса можно полу­чить, заменив в уравнениях адиабатного процесса показатель степени k на показатель n: Изменение внутренней энергии в политропном процессе для произвольной массы вещества определяется по формуле

Работа изменения объема в политропном процессе для 1 кг рабочего тела рав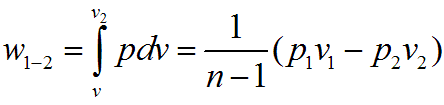на или, учитывая уравнение состояния Клапейрона,

Для произвольной массы газа

Количество теплоты в политропном процессе для m кг вещества определяется выражением, полученным в соответствии с первым законом термодинамики

Задание: записать в отчет данные о термодинамических процессах