
Функции нескольких переменных.
Основные понятия и определения.
Определение. Переменная величина Z называется функцией двух переменных величин х и у, если каждой паре значений х и у соответствует единственное значение z.
Функция двух переменных обозначается таким образом: Z = f ( х, у ).
Систему значений х и у называют точкой М(х,у), а функцию двух переменных – функцией точки: Z = f ( М ).
Геометрическим изображением функции двух переменных является некоторая поверхность в пространстве. Значение функции Z = f ( х, у ) при х =а, у = в обозначается f ( а, в ).
Определение. Переменная величина U называется функцией трех переменных х, у, z, если каждой тройке значений х, у и z соответствует единственное значение U.
Обозначение: U = f (х, у, z).
Аналогично для n переменных: U = f (х, у, z,…….., t).
Замечание: Для обозначения независимых переменных и функций могут быть использованы различные символы.
Например, функцию двух переменных можно записать в виде
у = f (х1, х2), а функцию n переменных – в виде: у = f (х1, х2, …….., хn ).
Определение: Функция n независимых переменных, устанавливающая зависимость между затратами n производственных ресурсов и объемом выпускаемой продукции, называется n- факторной производственной функцией (функцией выпуска): у = F(х1, х2, …….., хn ).
При моделировании экономики страны рассматривают следующую макроэкономическую двухфакторную производственную функцию: Y = F ( K , L ), где L – затраты труда, K – объем производственных фондов.
Определение. Совокупность всех точек, в которых определена функция нескольких переменных, называется областью определения функции.
Для функции двух переменных областью определения является некоторая часть координатной плоскости, ограниченная одной или несколькими линиями, для функции трех переменных – часть пространства.
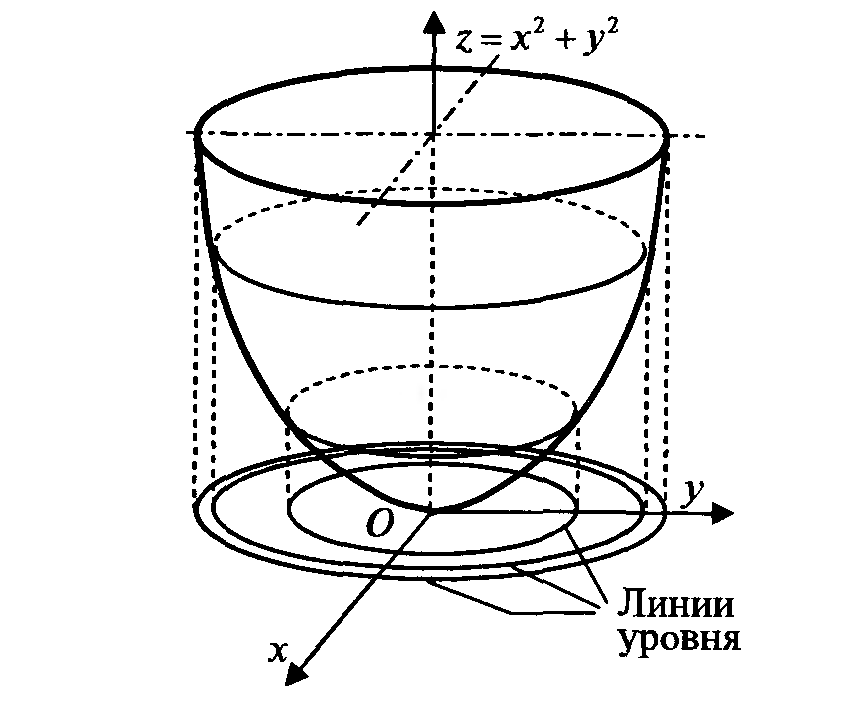
Определение. Линией уровня функции z = f (х, у) называется линия на плоскости ОХУ, в точках которой функция сохраняет постоянное значение.
Определение. Линии уровня производственных функций называются линиями постоянного выпуска или изоквантами.
Изокванты используются в задачах экономической теории.
Частные производные и полный дифференциал.
Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению данной переменной, когда последнее приращение стремится к нулю.
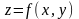 ,
,
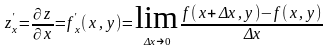 - частная
производная по х.
- частная
производная по х.
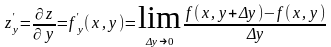 -
частная
производная по y.
-
частная
производная по y.
При нахождении частной производной пользуются правилами дифференцирования функции одной переменной, считая все другие аргументы постоянными.
Для функции нескольких переменных можно определить производные от производных, т.е. производные высших порядков.
Для производных второго порядка функции приняты следующие обозначения:
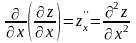 - функция
дифференцируется по x
последовательно два раза, считая y
постоянной величиной;
- функция
дифференцируется по x
последовательно два раза, считая y
постоянной величиной;
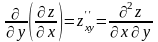 - функция сначала
дифференцируется по x,
а затем результат дифференцируется по
y;
- функция сначала
дифференцируется по x,
а затем результат дифференцируется по
y;
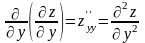 - функция
последовательно дифференцируется по
y
два раза.
- функция
последовательно дифференцируется по
y
два раза.
Следует
иметь в виду, что
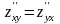 при условии, что они непрерывны.
Производные
при условии, что они непрерывны.
Производные
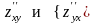 называются смешанными.
называются смешанными.
Аналогично вводятся частные производные 3-го и т.д. порядков.
Полный
дифференциал функции
вычисляется
по формуле:
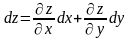 ,
причем
,
причем
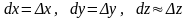 .
.
Пример.
Найти полный дифференциал функции
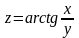 .
.
Решение. . Найдем частные производные.
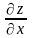 - вычислим производную
по x,
считая y
постоянным.
- вычислим производную
по x,
считая y
постоянным.
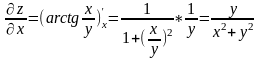 .
.
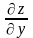 - вычислим производную
по y,
считая x
постоянным.
- вычислим производную
по y,
считая x
постоянным.
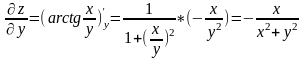 .
.
Тогда
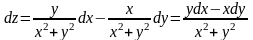 .
.
