
Лекция 6. Производная и дифференциал функции
Цель: Ввести понятие производной одной и нескольких переменных функций. Изучить необходимые правила и формулы производных функций. Освоить понятие дифференциала функции, знать его свойства, уметь найти дифференциал любой функции.
Ключевые слова: производная функции, дифференциал функции, частные производные и полный дифференциал.
План лекции
Производные элементарных функций.
Производная сложной функции и обратной функции.
Производные высших порядков.
Дифференциал функции.
Функции нескольких переменных.
Частные производные. Полный дифференциал.
Производные элементарных функций.
Дадим
аргументу х0
приращение
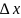 и перейдем на кривой
от
точки
и перейдем на кривой
от
точки
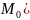 )
к точке
)
к точке
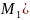 .
Проведем
секущую
.
Проведем
секущую
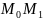 (см.рис.
1).
(см.рис.
1).
Под
касательной к кривой
 в точке естественно понимать предельное
положение
секущей
при
приближении
точки
в точке естественно понимать предельное
положение
секущей
при
приближении
точки
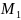 к
точке
к
точке
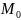 ,
т.е.
при
,
т.е.
при
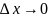 .
.
У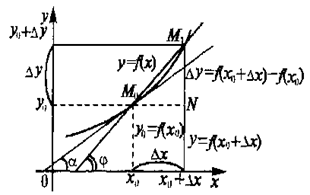 равнение
прямой, проходящей через точку
,
имеет вид
равнение
прямой, проходящей через точку
,
имеет вид
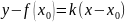 .
.
Рис.1
Угловой
коэффициент (или
тангенс угла
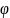 наклона)
наклона)
секущей
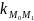 может
быть найден из
может
быть найден из
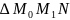 :
: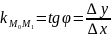 (см. Рис.1). Тогда угловой коэффициент
касательной
(см. Рис.1). Тогда угловой коэффициент
касательной
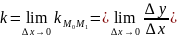 .
(1)
.
(1)
Пусть
функция
определена на промежутке X.
Возьмем точку
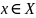 . Дадим значению х
приращение
. Дадим значению х
приращение
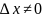 ,
тогда функция
получит
приращение
,
тогда функция
получит
приращение
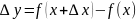
Определение. Производной функции предел отношения приращения функции к приращению аргумента при стремления последнего к нулю ( если этот предел существует и конечен)
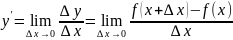
Нахождение производной функции называется дифференцированием этой функции.
Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка X, называется дифференцируемой па этом промежутке.
Действие нахождения производной называется дифференцированием, а функция, имеющая конечную производную, называется дифференцируемой.
Геометрический и экономический смысл производной.
Геометрический
смысл производной:
производная
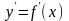 есть угловой коэффициент касательной,
проведенной к кривой
в точке
есть угловой коэффициент касательной,
проведенной к кривой
в точке
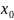 ,
т.е. .
,
т.е. .
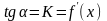 .
.
Экономический смысл производной.
Пусть
предприятие выпускает однородную
продукцию. Тогда издержки производства
y
можно считать функцией количества
выпускаемой продукции x,
y=f(x).
Предположим, что количество выпускаемой
продукции изменилось на
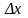 ,
тогда издержки производства изменяются
на
,
тогда издержки производства изменяются
на
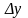 :
:
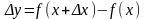 .
.
Разделим
приращение издержек производства на
приращение выпускаемой продукции:
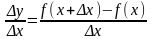 .
Это равенство выражает среднее приращение
издержек производства на единицу
приращенной продукции, перейдем к
пределy,
.
Это равенство выражает среднее приращение
издержек производства на единицу
приращенной продукции, перейдем к
пределy,
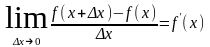 .
.
Этот
предел в экономике называется предельными
издержками производства. Таким
образом, производная
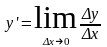 выражает
предельные издержки производства и
характеризует приближенно дополнительные
затраты на производство единицы
дополнительной продукции.
выражает
предельные издержки производства и
характеризует приближенно дополнительные
затраты на производство единицы
дополнительной продукции.
Аналогичным образом могут быть определены предельная выручка, предельный доход, предельный продукт, предельная полезность и другие предельные величины.
Зависимость между непрерывностью и дифференцируемостью функции.
Функция
y=f(x)
называется непрерывной
в точке, если
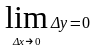 .
Функция y=f(x)
называется дифференцируемой в точке,
если она имеет производную, т.е.
.
Функция y=f(x)
называется дифференцируемой в точке,
если она имеет производную, т.е.
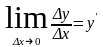
Между этими понятиями существует связь.
Теорема: Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна. Обратное утверждение неверно: непрерывная функция может не иметь производной.
Следствие: Если функция не является непрерывной в некоторой точке, то она не имеет производной в этой точке.
Основные правила дифференцирования.
Производная постоянной величины равна 0.
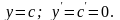
Производная алгебраической суммы нескольких дифференцируемых функций равна сумме производных этих функций.
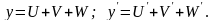
Производная произведения двух дифференцируемых функций равна сумме произведения каждой функции на производную другой функции.
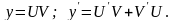
Следствия:
а) Постоянный множитель можно выносить за знак производной.
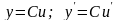
б) Производная произведения любого числа дифференцируемых функций равна сумме произведения производной каждой функции на произведение всех остальных функций.
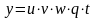 ;
;
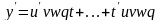
Производная частного равна производной числителя, умноженной на знаменатель, минус производная знаменателя, умноженная на числитель, и все это деленное на квадрат знаменателя.
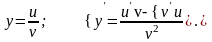
Следствия:
1)
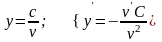 ;
2)
;
2)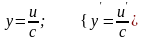 .
.
