
- •Лекция 5. Функция. Предел.Непрерывность.
- •Понятие функции. Способы задания функции
- •Классификация функций.
- •Монотонные функции.
- •Предел числовой последовательности.
- •Ограниченные последовательности.
- •Арифметические действия над сходящимися последовательностями.
- •Монотонные последовательности
- •Предел функции.
- •Арифметические действия над пределами функций.
- •Правило арифметических действий над пределами
- •Основные теоремы о пределах.
- •Замечательные пределы.
- •Некоторые замечательные пределы.
- •Непрерывность функции.
- •Тогда функция у принимает соответствующее значение f(x1).:
- •Точки разрыва и их классификация
Предел функции.
Определение.
Будем говорить, что f
имеет в точке
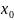 предел
предел
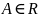 ,
если
,
если
 .
.
При этом примем обозначения
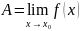
Смысл
определения предела функции
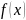 в
точке
состоит в том, что для всех значений
в
точке
состоит в том, что для всех значений
 ,
достаточно близких к
,
значения
функции
как
угодно мало отличаются от числа А
(по абсолютной величине).
,
достаточно близких к
,
значения
функции
как
угодно мало отличаются от числа А
(по абсолютной величине).
Рассмотрим геометрический смысл предела функции в точке. Неравенство
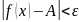
равносильно
двойному неравенству

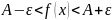
соответствующему
расположению части графика в полосе
шириной
 (см.
рис.
1).
Аналогично неравенство
(см.
рис.
1).
Аналогично неравенство
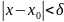 равносильно
равносильно
 двойному
неравенству
двойному
неравенству
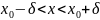 ,
соответствующему
попаданию
точек
х
в
,
соответствующему
попаданию
точек
х
в
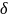 -окрестность точки х0.
-окрестность точки х0.
Число
А
есть предел функции
при
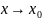 ,
если для любого
,
если для любого
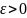 найдется такая
-окрестность точки х0,
что для всех
найдется такая
-окрестность точки х0,
что для всех
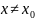 из
этой
окрестности соответствующие ординаты
графика функции
будут
заключены в полосе
,
какой
бы узкой эта
Рис.1 полоса
ни была.
из
этой
окрестности соответствующие ординаты
графика функции
будут
заключены в полосе
,
какой
бы узкой эта
Рис.1 полоса
ни была.
Арифметические действия над пределами функций.
Пусть
даны функции f
и g
и![]()
Суммой функцией f и g называется функция f+g, следующего вида
![]()
Произведением функцией f и g называется функция fg, следующего вида
![]()
Если
![]()
![]() то частное
то частное
![]() от функции f
на g
есть функция, определенное равенством
от функции f
на g
есть функция, определенное равенством
![]()
Правило арифметических действий над пределами
Пусть
![]()
![]()
![]()
![]() Тогда при условии, что операция имеет
смысл для пределов a
и b
справедливы равенства
Тогда при условии, что операция имеет
смысл для пределов a
и b
справедливы равенства
![]()
Основные теоремы о пределах.
Теорема. Предел алгебраической суммы конечного числа слагаемых равен сумме пределов этих слагаемых.
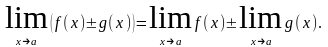
Теорема. Предел произведения любого конечного количества сомножителей равен произведению их пределов.

Теорема. Предел частного двух переменных равен частному их пределов, если только предел знаменателя отличен от нуля.
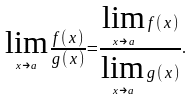
Следствие 1. Постоянный множитель можно выносить за знак предела.
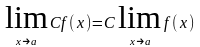 .
.
Следствие 2 . Предел степени переменной равен той же степени предела переменной.
 .
.
Примеры. Найти предел функции.
1)
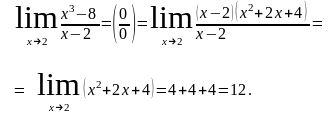
2)
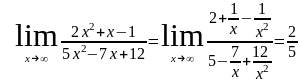
Замечательные пределы.
Теорема. Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен 1.
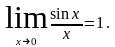
Этот предел называется первым замечательным пределом.
Пример.
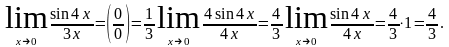
Теорема.
Последовательность
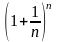 при
при
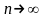 ,
имеет предел, заключенный между числами
2 и 3.
,
имеет предел, заключенный между числами
2 и 3.
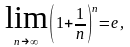 где
е =
2,71828…
где
е =
2,71828…
Этот предел называется вторым замечательным пределом.
Число е является основанием логарифмов, которые называются натуральными логарифмами и обозначаются lnx
Пример.
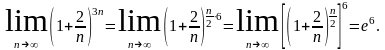
Если обозначить 1/n = α, то второй замечательный предел запишется в виде:
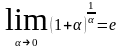
Пример.
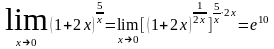
Некоторые замечательные пределы.
1)
![]()
2)
![]() ,
,
![]() .
.
3)
![]()
![]()
![]()
3’)![]()
4)
![]()
![]()
![]()
5)
![]()
![]()
6)
![]()
![]()
![]()
Примеры:
1)
![]()
![]()
2)![]()
3)
![]()
![]()
![]()
В итоге
![]()
![]()
Непрерывность функции.
Пусть функция y=f(x) определена в точке х=х0 и ее окрестности. Придадим аргументу новое значение х1.
Величина х1-х0 называется приращением аргумента.
х1-х0=Δх, х1=х0+ Δх
