1.4.6. Пересечение прямой общего положения с плоскостью общего положения

В предыдущих пунктах мы рассмотрели случаи пересечения прямой и плоскости при частном расположении пересекающихся фигур. Теперь обратимся к решению одной из главных позиционных задач: нахождение точки пересечения прямой общего положения с плоскостью общего положения.

Построим точку К - точку пересечения прямой общего положения а с плоскостью общего положения b, заданную тремя точками А, В, С.

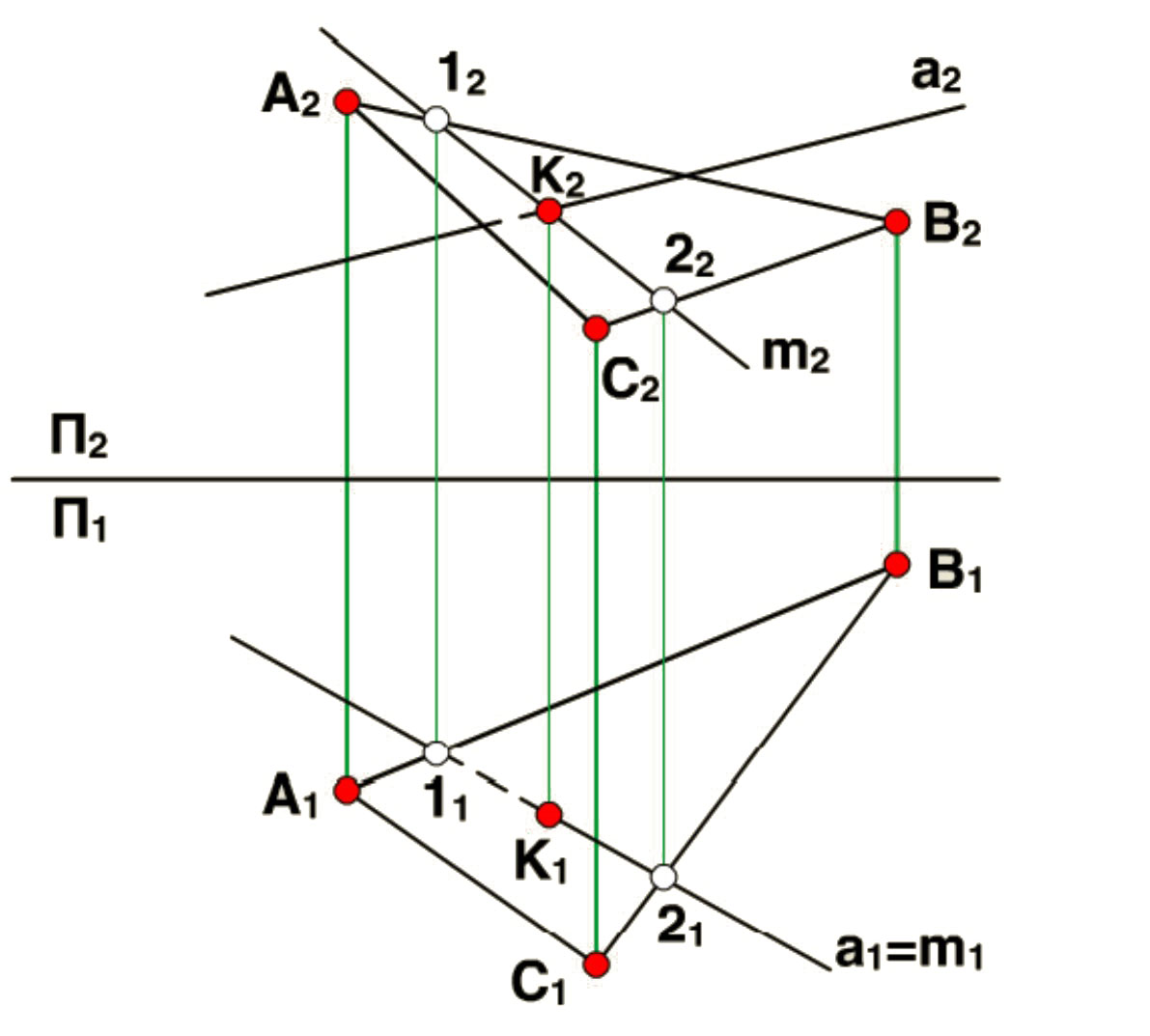
Алгоритм построения точки пересечения:

Например на П1 проведем через заданную прямую а1 вспомогательную горизонтально проецирующую плоскость s1: а s и s П1.

Построим m1 - линию пересечения вспомогательной плоскости s1 с заданной плоскостью b1. Отметим точки 11 и 21 - точки пересечения прямой m1 и отрезков А1В1 и В1С1 соответственно.

Построим фронтальную проекцию прямой m, учитывая принадлежность точек 1 и 2 сторонам треугольника АВС.

Находим точку К2 - точку пересечения прямых m2 и а2: К2=m2 а2.

По линии связи находим первую проекцию точки К - точку К1.

Определяем видимость прямой а с помощью метода конкурирующих точек. На П2, правая часть прямой а2 (относительно точки К2) - видима, а левая часть прямой а2 - невидима. На П1, левая часть прямой а1 (относительно точки К1) - невидима, а правая часть прямой а1 - видима.

1.4.7 Пересечение плоскостей общего и частного положения

Пусть нам дана плоскость частного положения a П1 и плоскость общего положения, заданная треугольником АВС. Требуется построить линию пересечения плоскости a с плоскостью АВС.

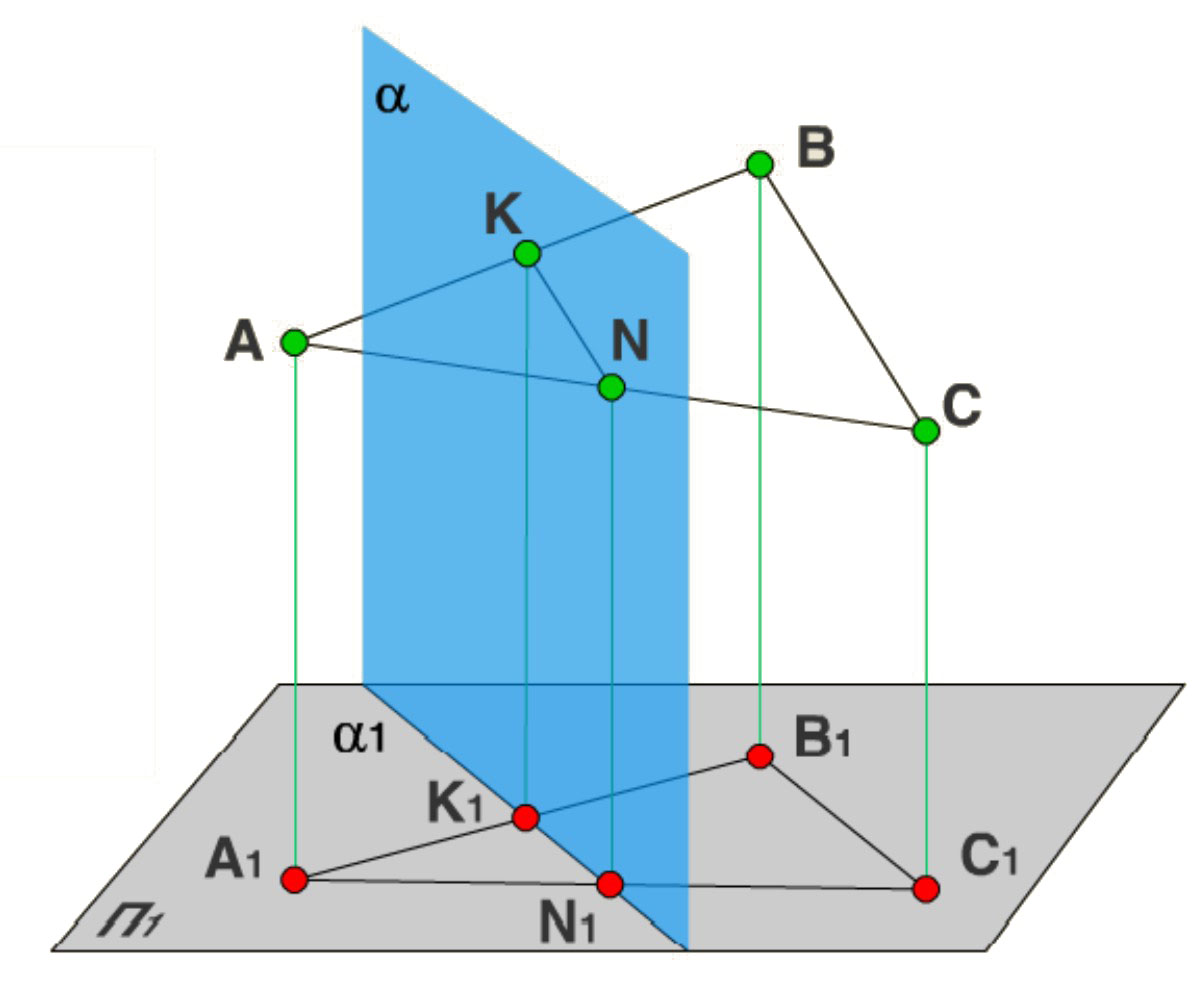
Рассмотрим сначала пространственную модель, на которой даны плоскость a, плоскость АВС и плоскость проекций П1. Спроецируем плоскости a и ABC на П1. Плоскость общего положения АВС проецируется на плоскость П1 в виде треугольника А1В1С1, а плоскость частного положения a - в виде прямой a1. На плоскости П1 прямая a1 и АВС пересекаются в точках K1 (K1 принадлежит А1В1) и N1 (N1 принадлежит А1C1). Если через точки K1 и N1 провести проецирующие прямые до пересечения с плоскостью АВС, то получатся две точки K (K принадлежит АВ) и N (N принадлежит АC). Соединив точки K и N, мы получим прямую KN. Прямая KN - линия пересечения плоскости a с плоскостью АВС.

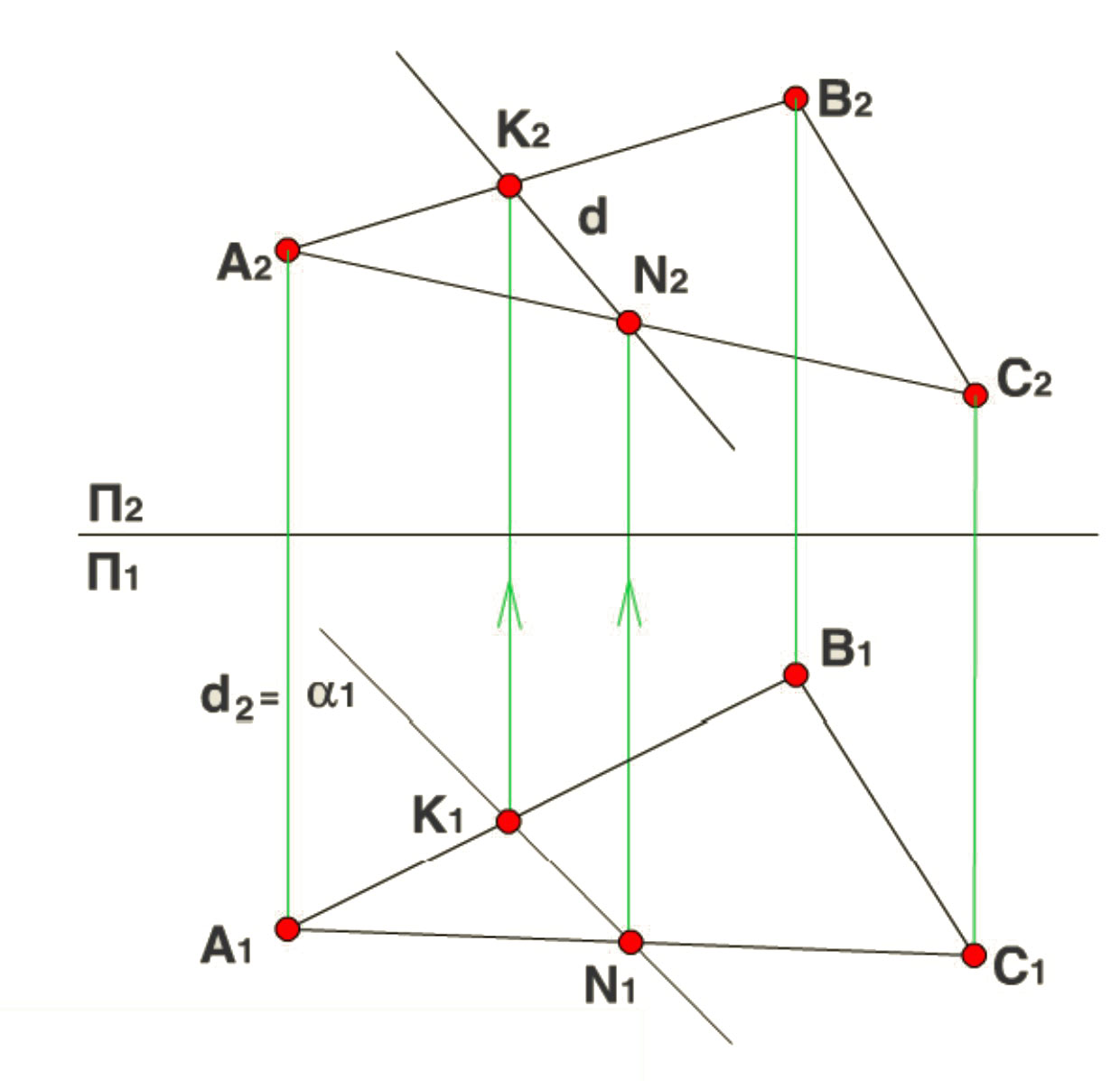
Теперь обратимся к комплексному чертежу. K1 принадлежит a1 , следовательно K принадлежит a. K1 принадлежит A1B1, а K2 принадлежит A2B2, следовательно K принадлежит AB. Из этих утверждений следует, что K - точка пересечения прямой АВ с плоскостью a. Возьмем точку N и проделаем те же действия. Теперь рассмотрим ABС (заданный пересекающимися прямыми АВ, АС). КN - линия пересечения плоскости ABС с плоскостью a.

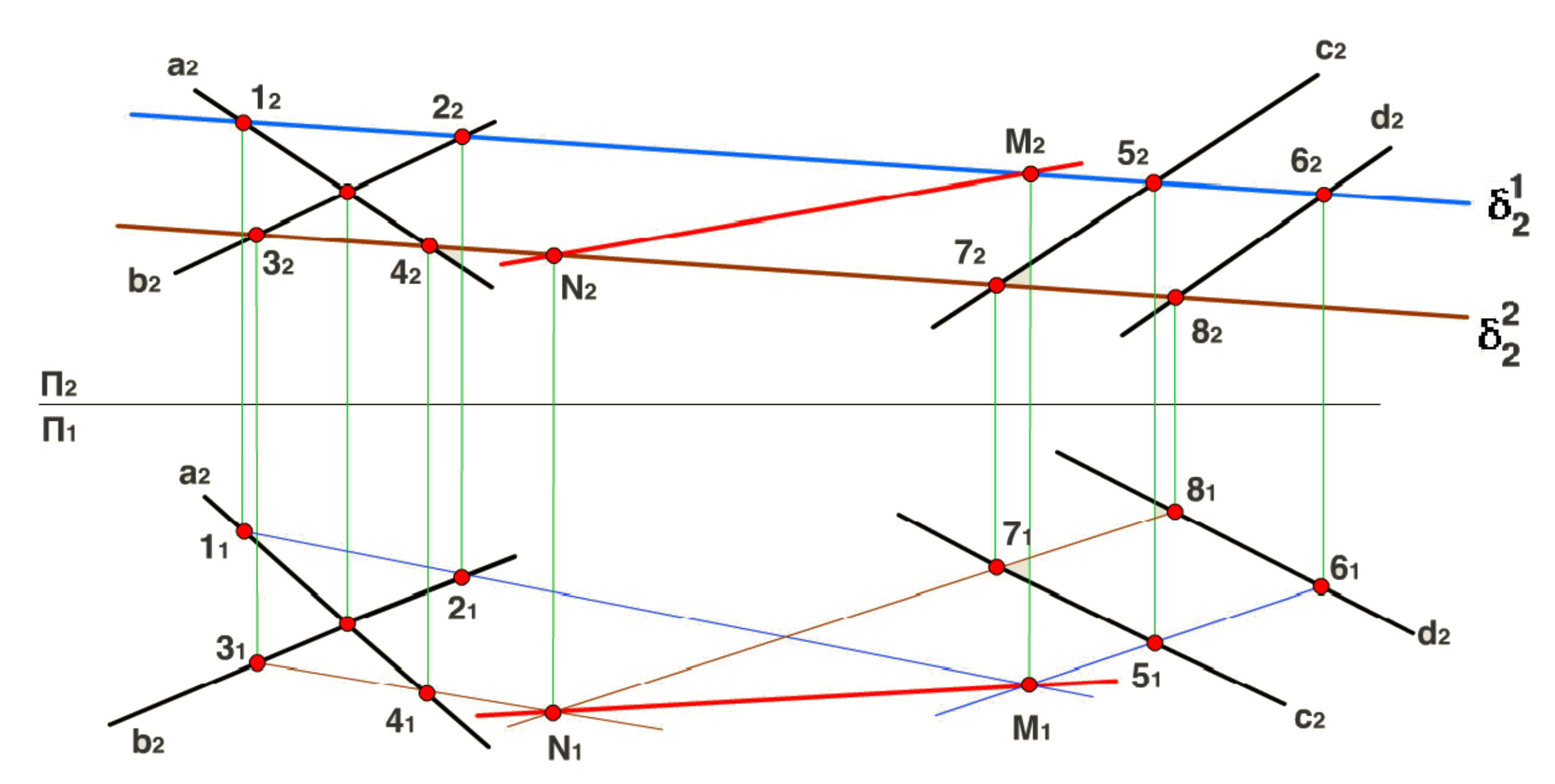
1.4.8. Пересечение двух плоскостей общего положения

Теперь рассмотрим пример пересечения двух плоскостей общего положения. Для построения линии пересечения двух плоскостей a и b необходимо найти две точки, N и M каждая из которых принадлежит обеим плоскостям. Для нахождения точек N и M можно воспользоваться следующим алгоритмом:

1. Взять две дополнительные плоскости частного положения 1ЧП и 2ЧП;

2. Определить линии пересечения плоскостей частного положения 1ЧП и 2ЧП с плоскостями общего положения a и b с помощью метода, приведенного в предыдущем пункте;

3. Определить точки N и M пересечения полученных линий.

Выполним построения:

1. Возьмем плоскости общего положения a и b. Плоскость a задана пересекающимися прямыми a и b. Плоскость b задана параллельными прямыми c и d.

2. Возьмем плоскости частного положения 1ЧП и 2ЧП перпендикулярные к П1.

3. Найдем точки пересечения 1ЧП и 2ЧП с прямыми, задающими плоскости a и b. Опустим линии связи и получим проекции линий пересечения плоскостей на П1.

4. Теперь найдем две точки N1 и M1 пересечения полученных линий (синие на чертеже). Обратите внимание, что нас интересуют точки пересечения тех линий, которые получены пересечением одной плоскости частного положения с двумя общего. То есть, например, точка N при таком построении является точкой пересечения линий пересечения 1ЧП с a и b и соответственно принадлежит и a и b.

5. Поднимаем линии связи и получаем вторые проекции точек M и N.

6. Точки M и N принадлежат одновременно a и b, поэтому MN - линия пересечения a и b.