1.4.4. Прямая, параллельная плоскости
Прямая параллельна плоскости, если она параллельна прямой, принадлежащей данной плоскости.
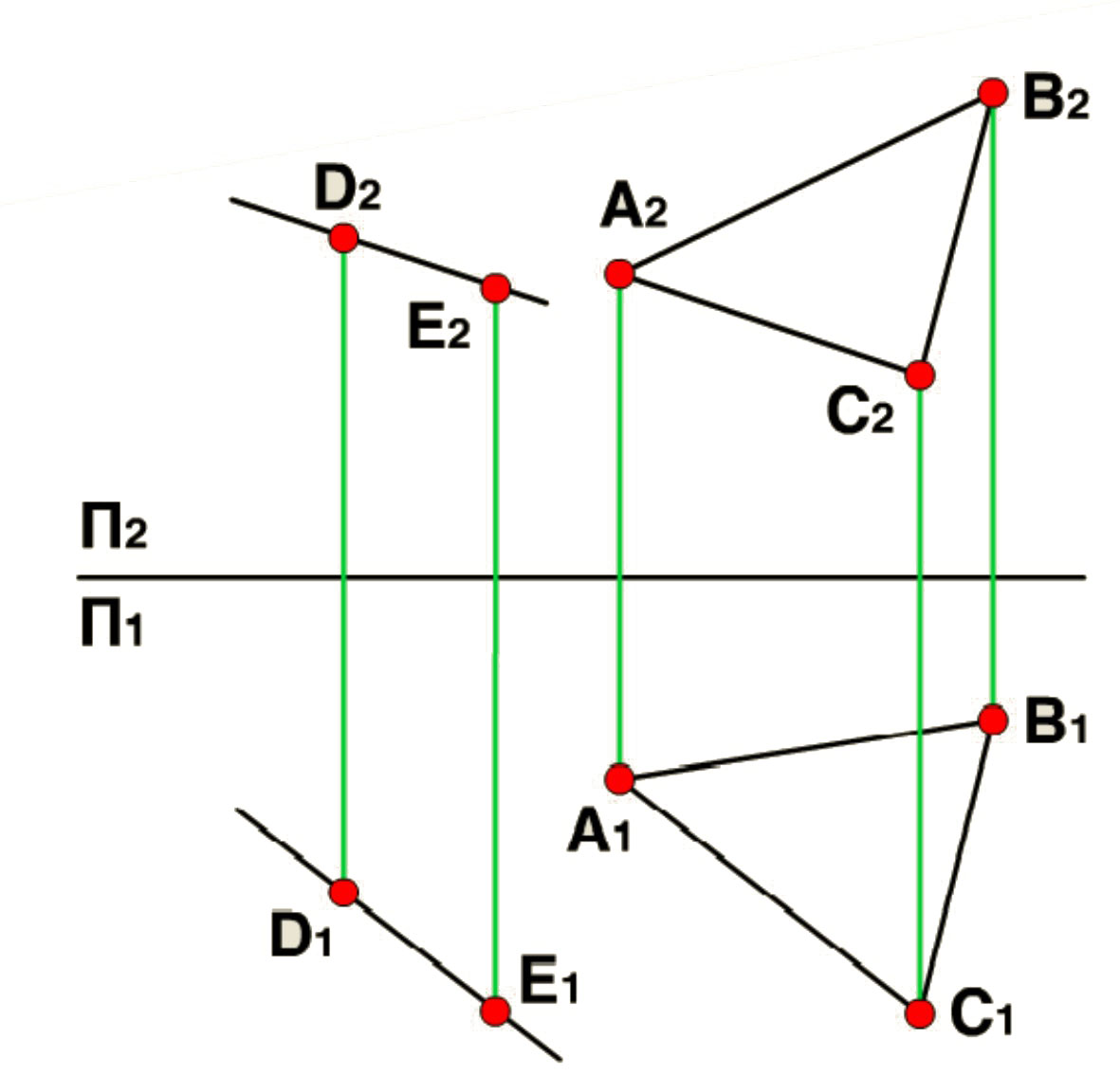
Рассмотрим пример. Пусть нам дана плоскость a заданная треугольником АВС и произвольная точка D. Требуется через точку D провести прямую DE параллельную плоскости a. Для того чтобы через точку D провести прямую параллельную плоскости a (АВС), достаточно построить прямую проходящую через точку D и параллельную любой прямой, принадлежащей плоскости a. Например, проведём прямую DE || AC, на чертеже D1E1 || А1С1 и D2E2 || А2С2. Прямая DE || a (АВС), т. к. она параллельна прямой АС, принадлежащей плоскости a.
1.4.5 Параллельные плоскости
Еcли две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.
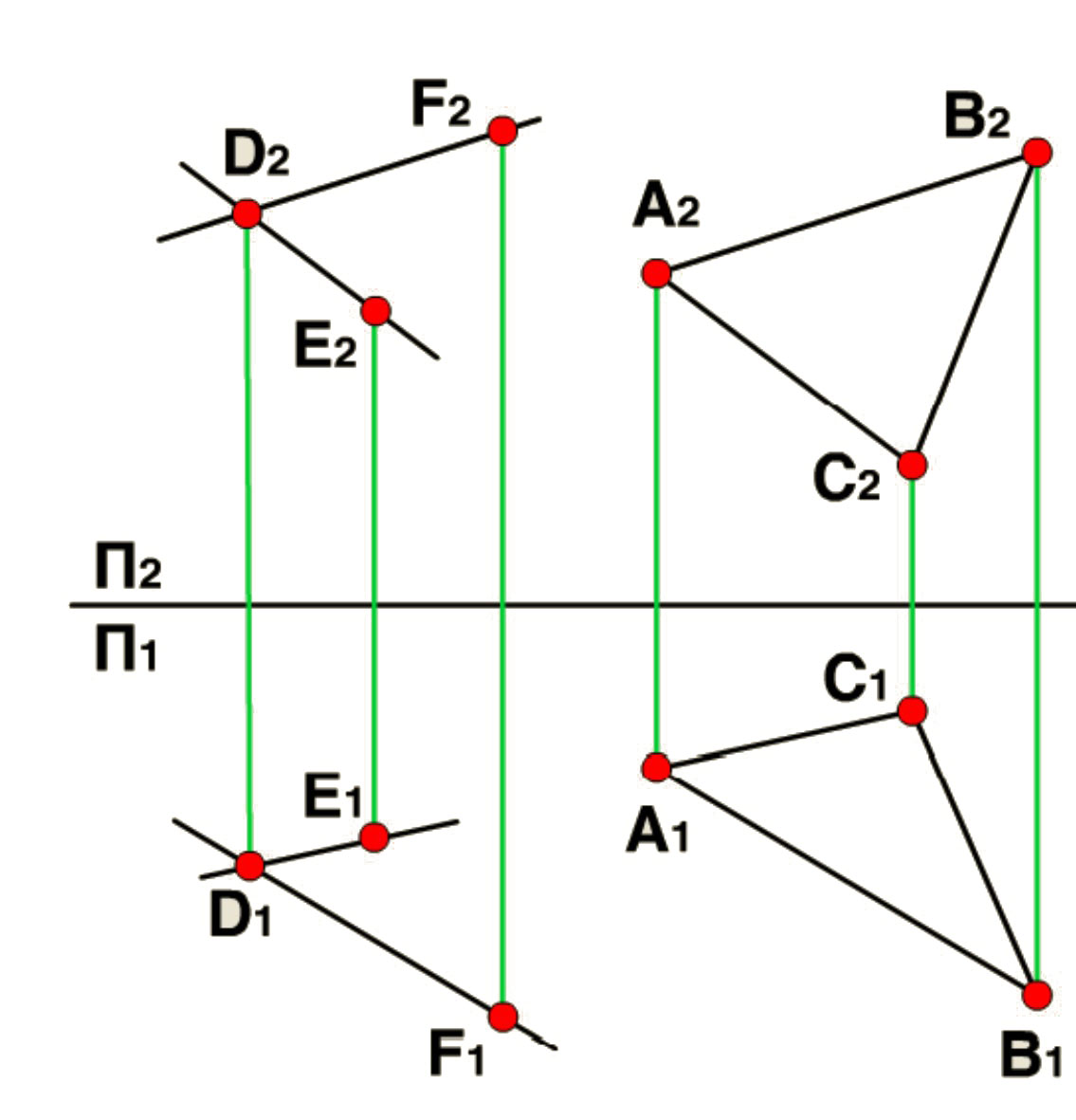
Рассмотрим пример. Пусть нам дана плоскость a, заданная треугольником АВС и произвольная точка D. Требуется через точку D провести плоскость b параллельную a (АВС). Для того чтобы через точку D провести плоскость параллельную плоскости a (АВС), достаточно построить две пересекающиеся прямые, параллельные двум пересекающимся прямым плоскости a, так чтобы точка D принадлежала этим прямым. Например, проведём прямую DE || AC, на чертеже D1E1 || А1С1 и D2E2 || А2С2 и прямую DF || AB, на чертеже D1F1 || А1B1 и D2F2 || А2B2. Две пересекающиеся прямые DE и DF определяют плоскость b. Плоскость b || a, так как две пересекающиеся прямые DE и DF, принадлежащие плоскости b, параллельны двум пересекающимся прямым АВ и АС, принадлежащим плоскости a.
1.4.5 Пересечение прямой общего положения с проецирующей плоскостью
Двумя основными позиционными задачами являются:
1. задача на пересечение прямой общего положения с плоскостью общего положения;
2. задача на пересечение двух плоскостей общего положения.
Прежде чем решать эти основные позиционные задачи рассмотрим частные случаи решения задач, т. е. решения позиционных задач при частном расположении пересекающихся фигур.
Рассмотрим построение проекций точки K - точки пересечения прямой а общего положения с фронтально проецирующей плоскостью s.
Плоскость s проецируется на П2 в виде прямой - s2, а на П1 первая проекция плоскости s совпадает с плоскостью П1.
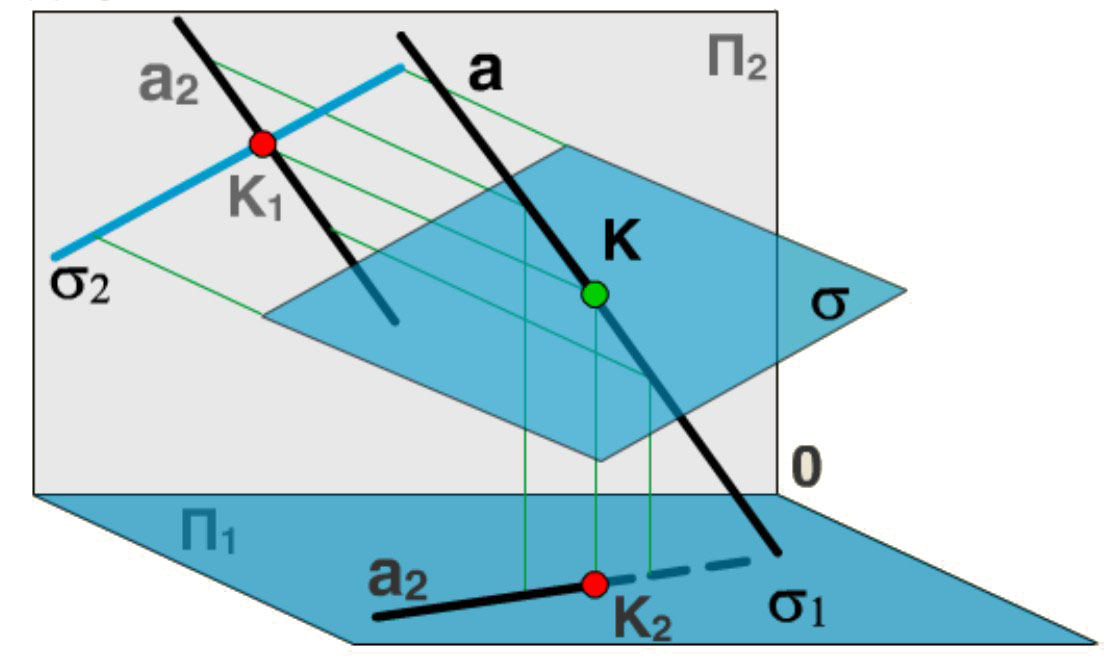
Вторая проекция точки К - К2 является точкой пересечения вырожденной проекции s2 плоскости s и а2 - второй проекции прямой а: а2 s2 = К2. Проекцию К1 находим по принадлежности точки К прямой а: К1 а1.
Дополним рисунок изображением видимых и невидимых участков прямой а, плоскость считаем непрозрачной. Левая полупрямая до точки К располагается выше плоскости s, а потому на П1 проекция этой части прямой видима до точки К1, другая часть прямой – невидима.
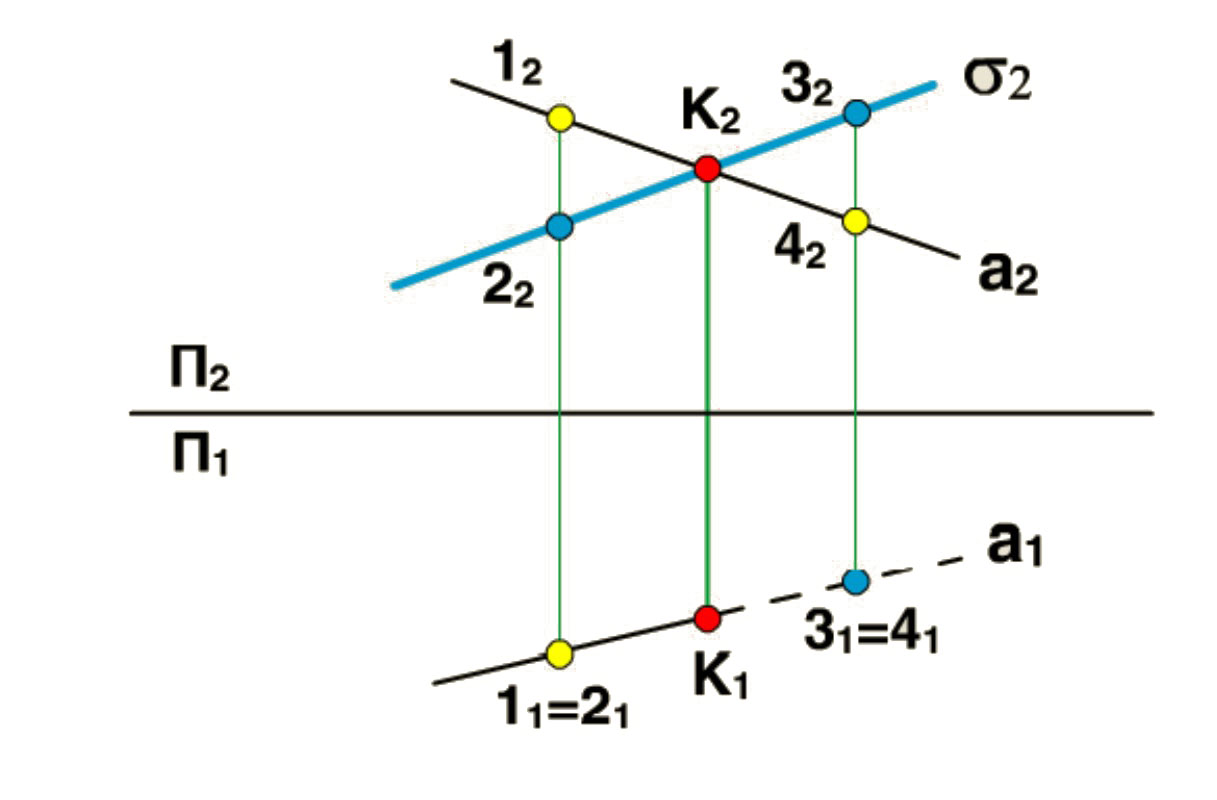
Теперь обратимся к ортогональному чертежу. Отметим на П2 точку К2 - точку пересечения s2 и а2.
Опустим из точки К2 линию связи на П1 и найдем точку пересечения с прямой а2. К1 - первая проекция точки К - точки пересечения плоскости s и прямой а.
Методом конкурирующих точек определим видимые и невидимые участки прямой а1.
1.4.5. Пересечение проецирующей прямой с плоскостью общего положения
Построим точку К - точку пересечения горизонтально проецирующей прямой а с плоскостью общего положения s, заданную тремя точками А, В, С.
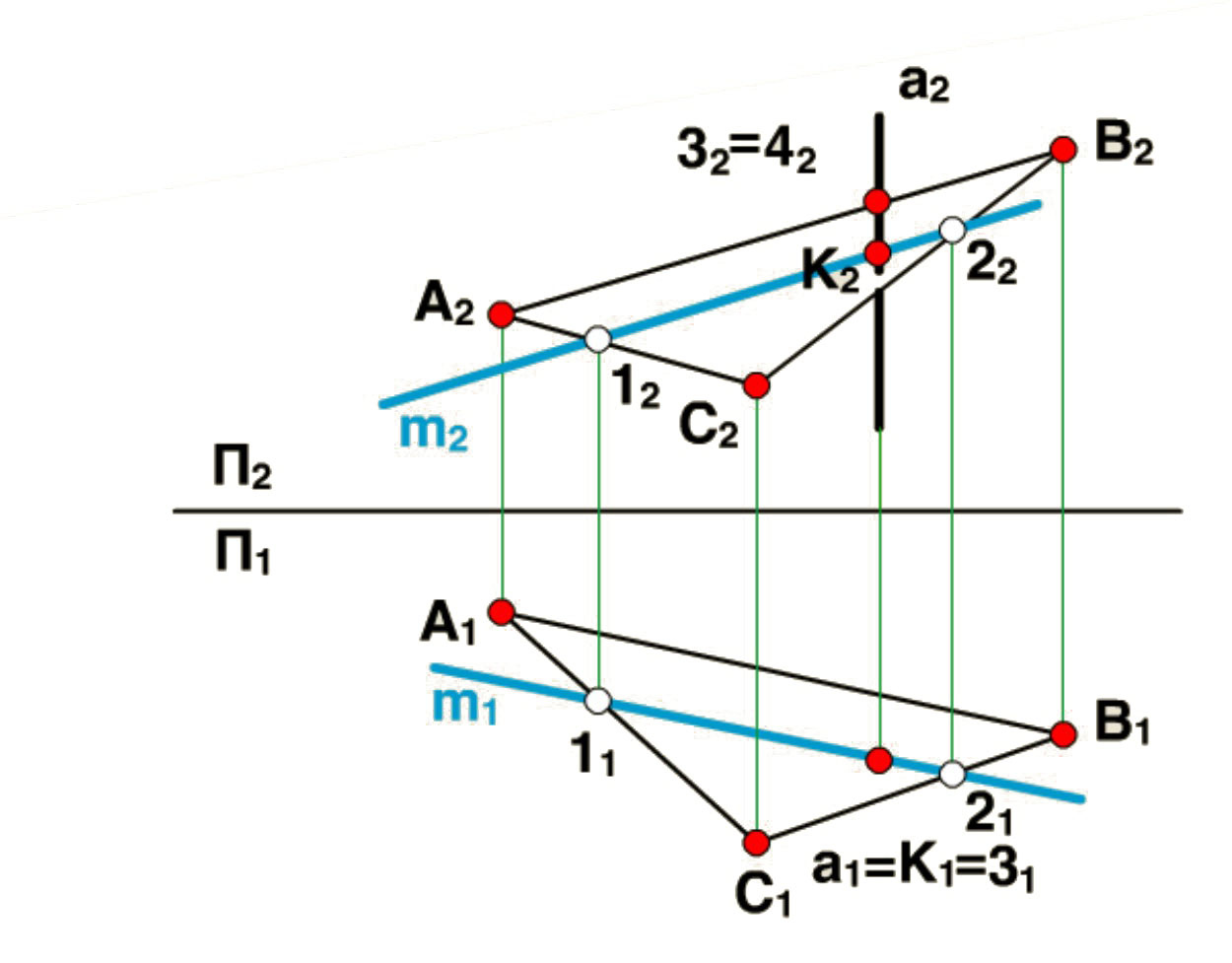
Горизонтальная проекция К1 точки К совпадает с вырожденной проекцией прямой а: а1 = К1.
Строим вторую проекцию К2 точки К по алгоритму:
Проводим в плоскости П1 прямую m1 через точку К1 и принадлежащую плоскости s. Точки 11 и 21 - точки пересечения прямой m1 и отрезков А1С1 и В1С1 соответственно.
Строим фронтальную проекцию прямой m, учитывая принадлежность точек 1 и 2 сторонам треугольника АВС.
Находим точку К2 - точку пересечения прямых m2 и а2: К2=m2 а2.
На ортогональном чертеже определяем видимость прямой а используя метод конкурирующих точек. На П2, та часть прямой а2, которая выше точки К2 - видима, а часть прямой а2, которая ниже точки К2 - невидима.