1.2.3 Трехпроекционный ортогональный чертёж точки

На практике при изображении сложных оригиналов, приходится увеличивать число плоскостей. Дополним систему плоскостей П1П2 плоскостью П3 совмещенной с ОYZ.

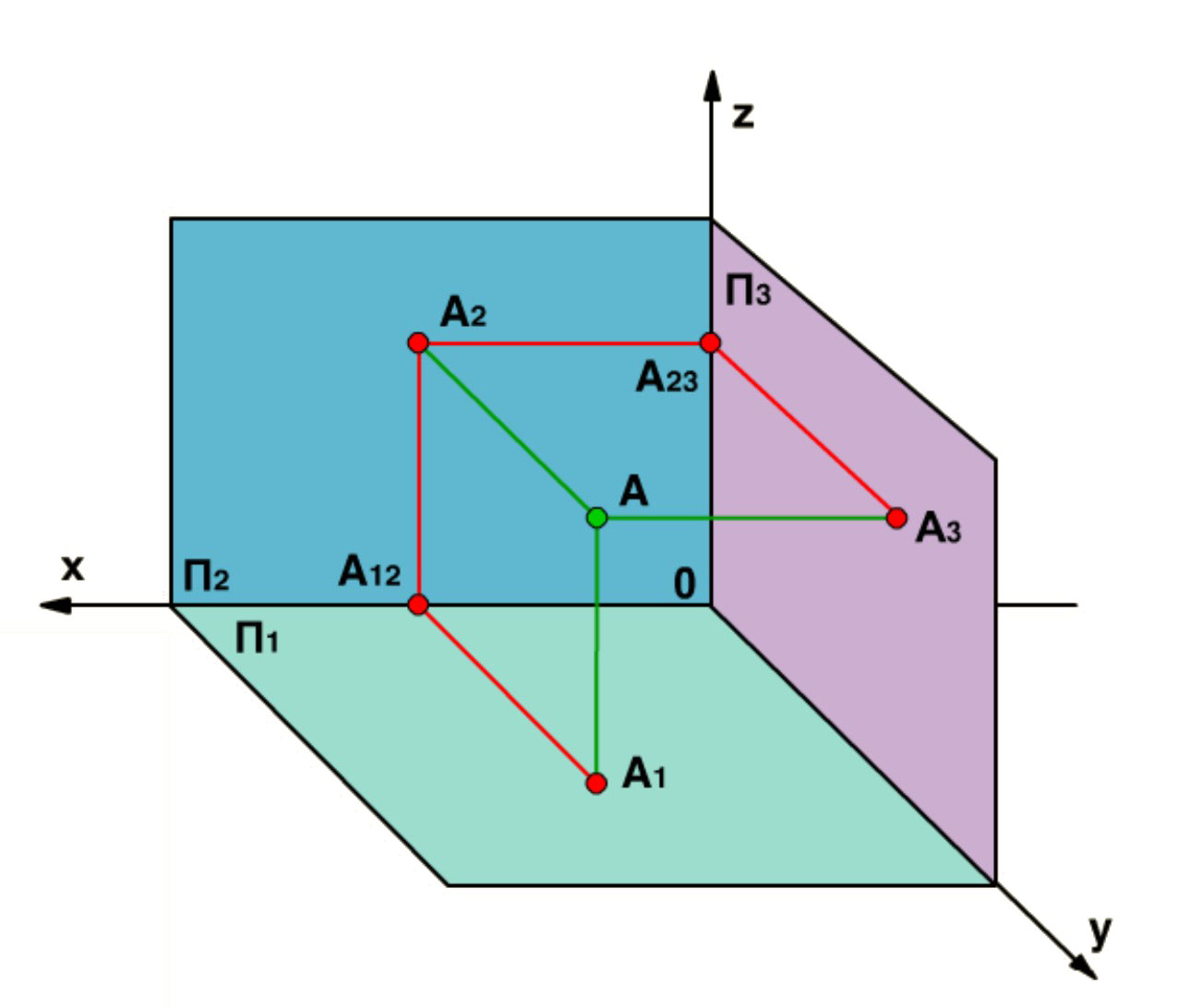
Построим проекцию точки А на эту плоскость, опустив из точки А перпендикуляр на П3. A3 - третья или профильная проекция точки А. Повернем плоскость П3 вокруг оси OZ до совмещения с плоскостью П2. В итоге плоскости П1, П2 и П3 совместились в одну плоскость.

На чертеже линии связи А2 А1 и А2 А3 к соответствующим осям: А2 А1 П2 / П1, а А2 А3 П2 / П3. Мы получили трёхпроекционный ортогональный чертёж точки А.

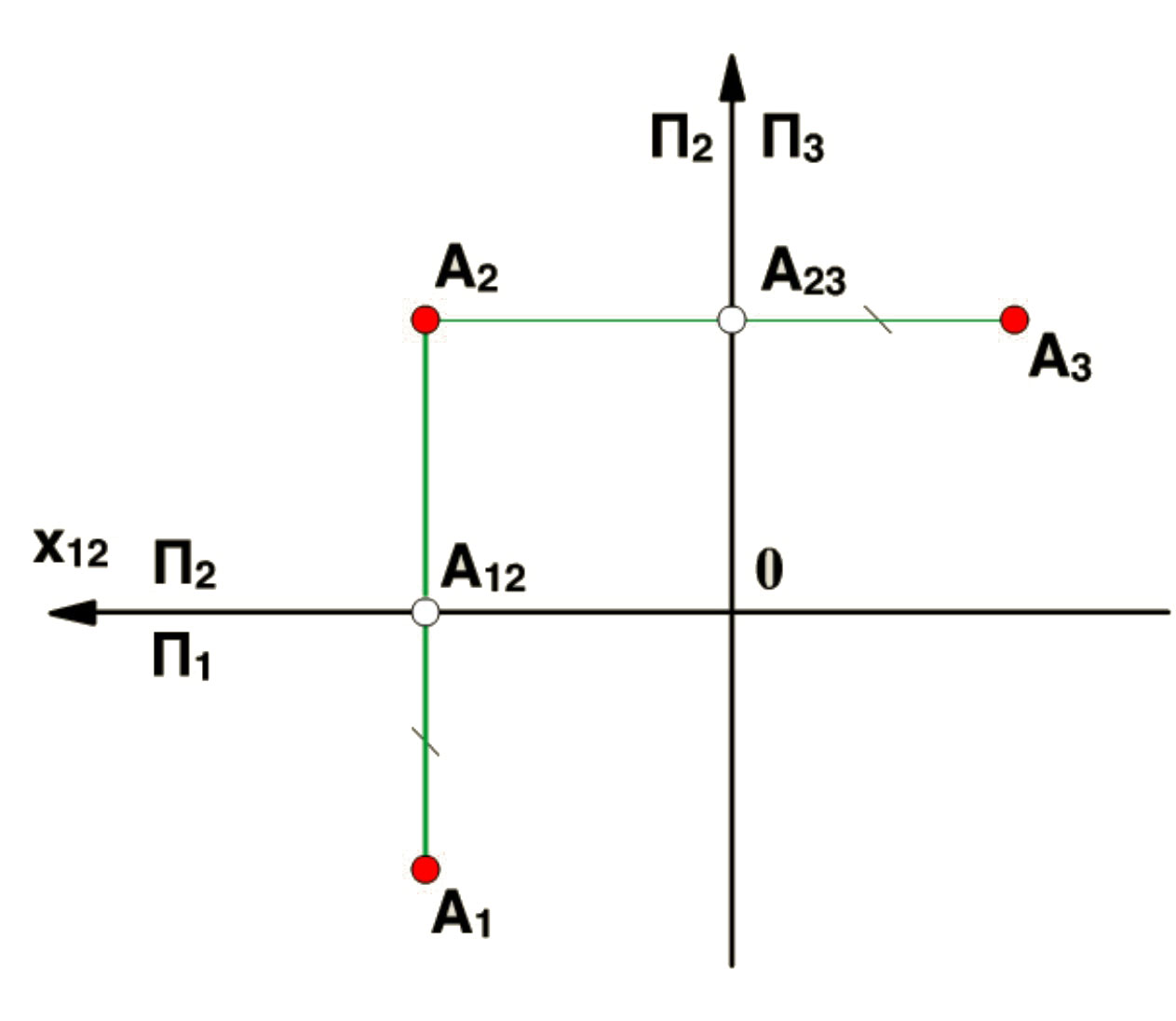
Расстояние от точки А1 и точки А3 до соответствующих осей проекций равны между собой и равны расстоянию от точки А до плоскости П2.

По ортогональному чертежу можно судить о расстоянии - r от точки А до плоскостей П1, П2 и П3:

- до П1: r = А2 А12= z (аппликате точки А)

- до П2: r = А1 А12=А3 А23= y (ординате точки А)

- до П3: r = А2 А23= x (абсциссе точки А)

Взаимосвязь между проекциями оригинала на комплексном чертеже заключается в следующем:

Две проекции точки располагаются на одной линии связи.

Линии связи между собой параллельны.

Две проекции точки определяют положение её третей проекции.

Итак, мы рассмотрели возможность решения обратной задачи начертательной геометрии, т. е. восстановление по ортогональному чертежу формы, размеров оригинала, взаимного расположения его элементов и других геометрических параметров.

1.2.4.Ортогональные проекции точки общего положения

По отношению к плоскостям проекций точка может занимать общее положение, т. е. ни принадлежать ни одной из плоскостей проекций, и частное положение - находиться на одной из этих плоскостей, сразу на двух плоскостях проекций и одновременно на трёх плоскостях.

В предыдущих пунктах мы рассмотрели ортогональные чертежи точки А - точки общего положения, находящейся в первой четверти. Теперь рассмотрим примеры ортогональных чертежей точек общего положения, расположенных во 2, 3 и 4 четвертях.

Чертежи точек, расположенных в различных четвертях, имеют различное положение проекций относительно оси Х12. Это зависит от знания координат Z и Y.

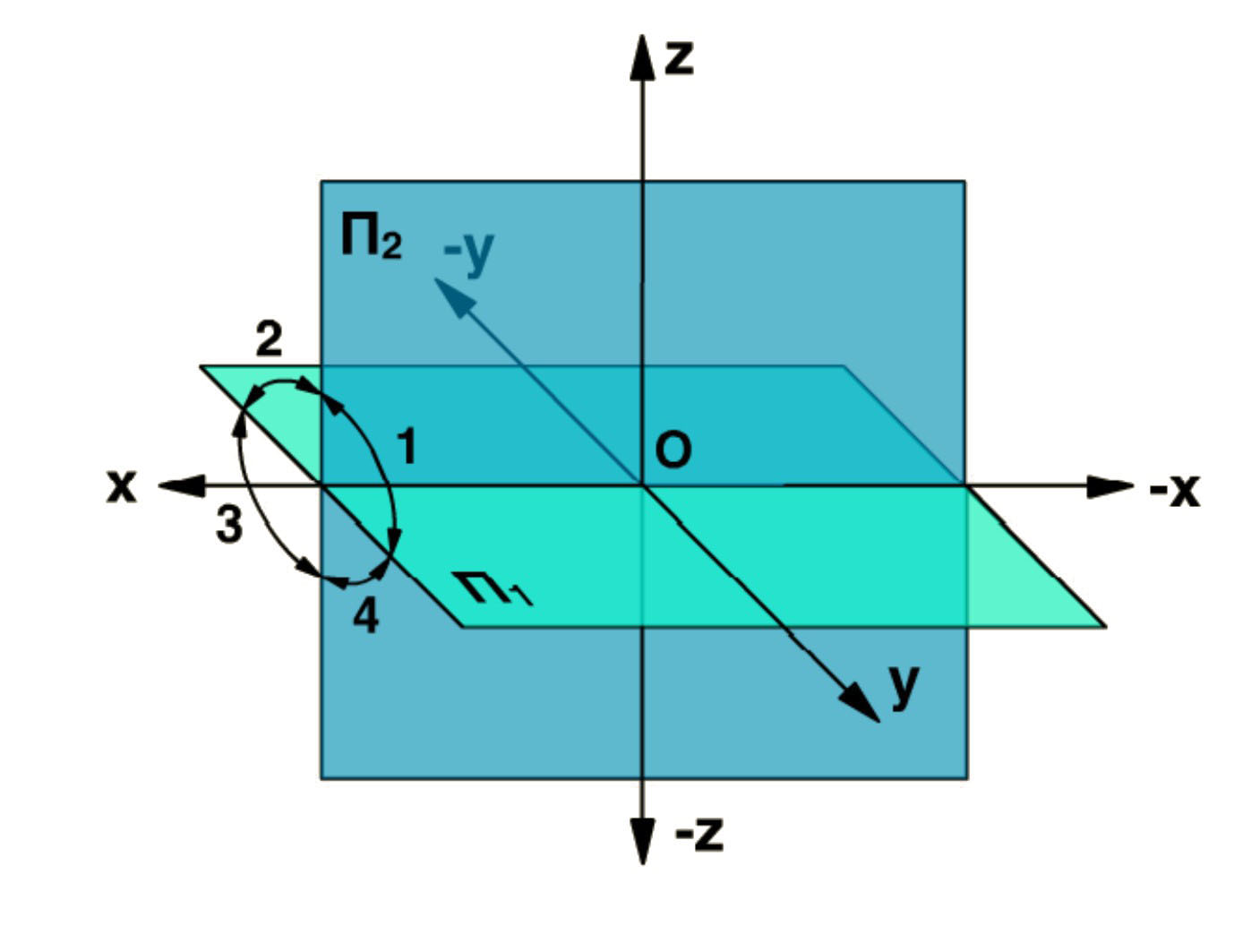
Точки A, B, C и D - точки общего положения, причем точка A находится в первой четверти, точка B - во второй, точка C - в третей, а точка D - в четвертой четверти.

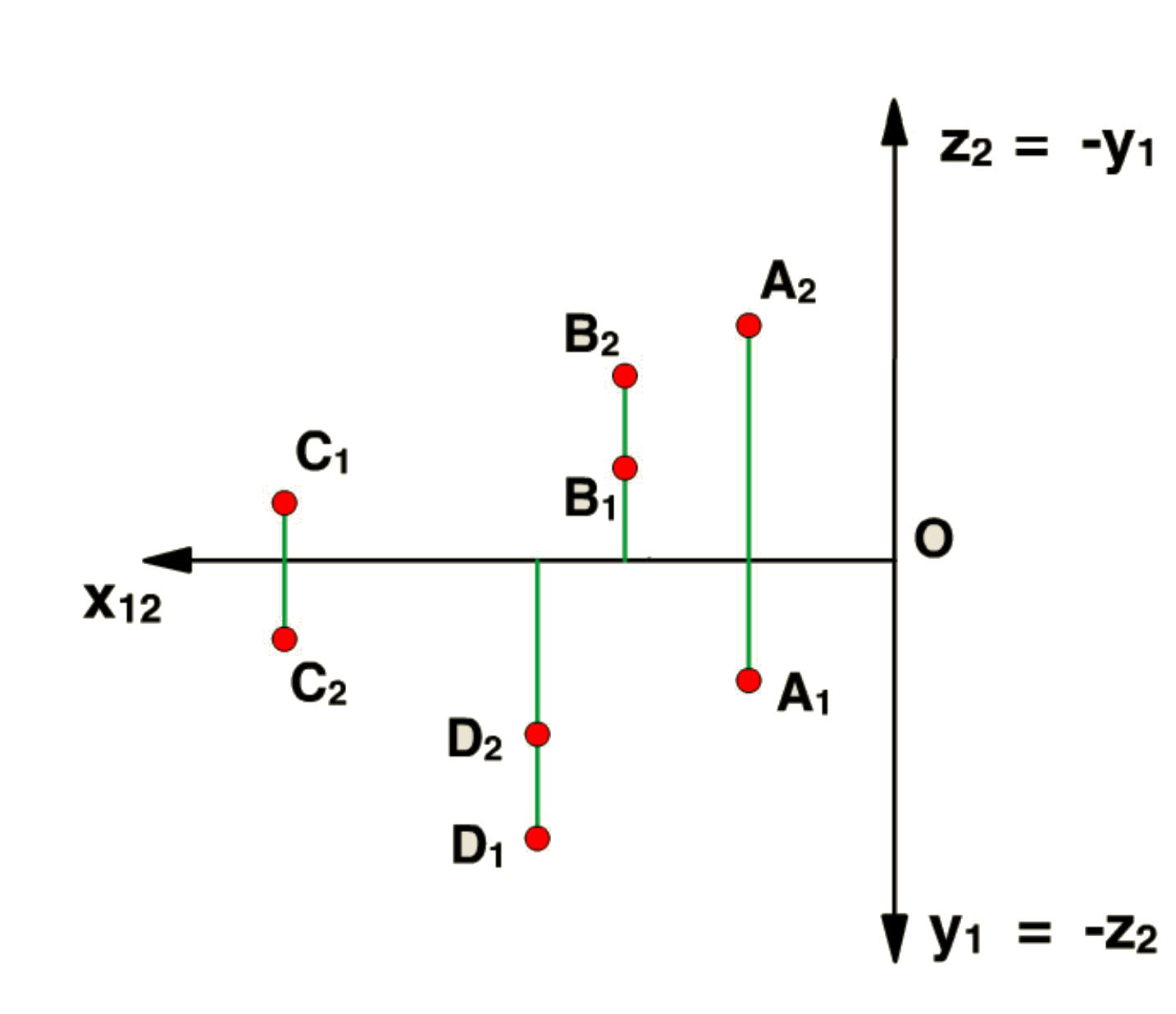
На ортогональном чертеже проекции точек A, B, C и D будут располагаться так, как представлено на рисунке.

1.2.5. Ортогональные проекции точки частного положения

Точка частного положения - точка, находящаяся на одной из плоскостей проекций, сразу на двух плоскостях проекций или одновременно на трёх плоскостях проекций.

Точки могут принадлежать плоскостям проекций и осям ОХ, ОY, ОZ. В этом случае одна или две координаты равны нулю. А потому одна или две проекции точки принадлежат осям координат.

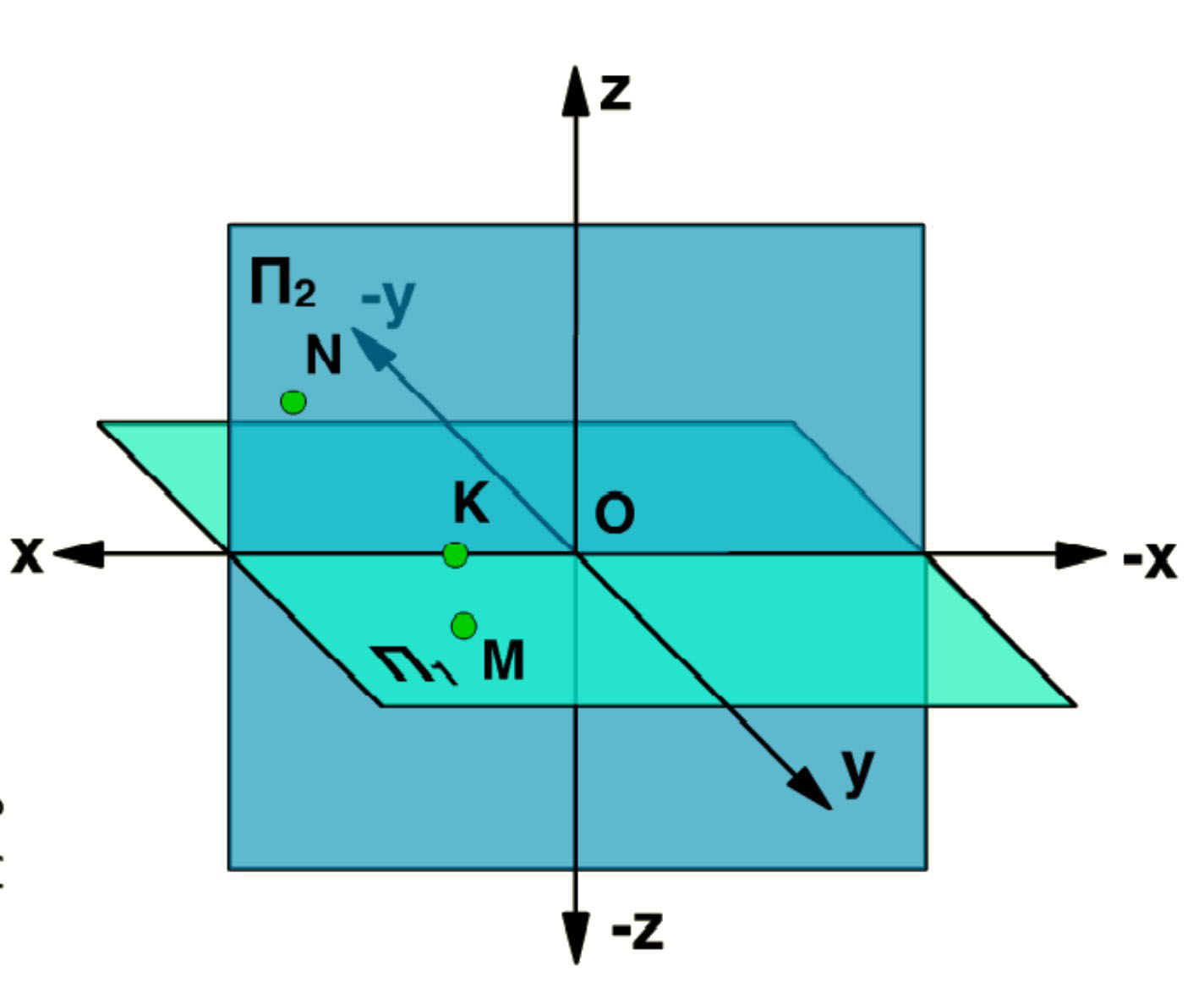
Точки N, M и K - точки частного положения. Точка N принадлежит плоскости П2, точка M принадлежит плоскости П1, а точка K принадлежит оси проекций ОХ, следовательно, принадлежит сразу обеим плоскостям.

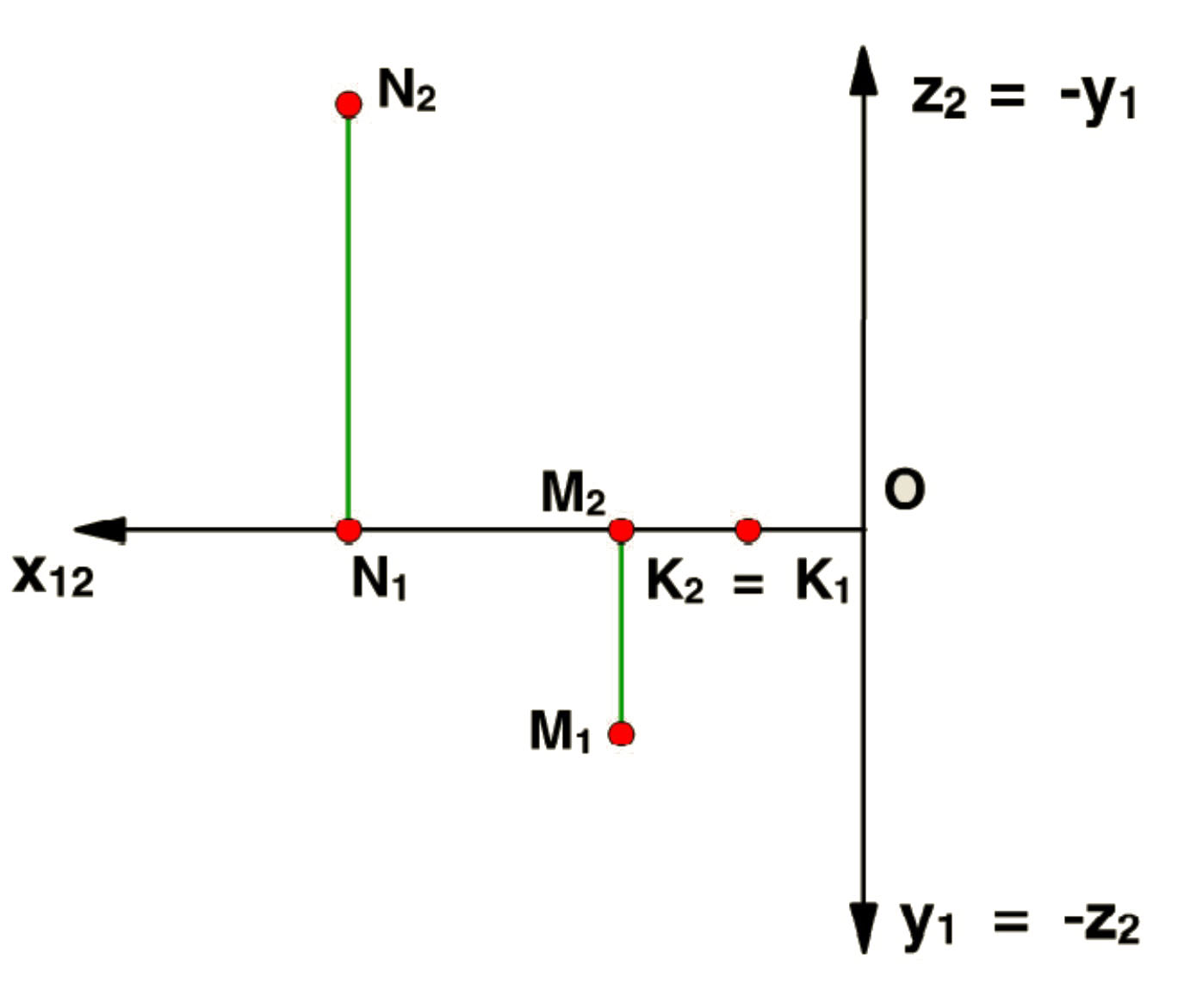
На ортогональном чертеже проекции точек N, M и K будут располагаться так, как представлено на рисунке.