3.1.3. Коническая поверхность
Коническая поверхность образуется при движении прямой, которые пересекаются в собственной точке S, называемой вершиной, и пересекают направляющую а.
Можно сказать, что коническая поверхность есть частный случай поверхности с ребром возврата, когда ребро возврата стягивается в точку S. Определитель поверхности Г (а, S) закон движения образующей: S li, li a.
Для наглядности построен каркас образующих. Если направляющая кривая 2-го порядка, то при движении прямой образуется конус 2-го порядка. Частным случаем является конус с направляющей окружностью, когда все направляющие одинаково наклонены к плоскости окружности.
На рисунке показано задание конической поверхности на ортогональном чертеже.
3.1.4 Цилиндрическая поверхность
Цилиндрическая поверхность получается в том случае, когда прямолинейная образующая при движении пересекает направляющую а и остается параллельной сама себе и указанному направлению S, стремящемуся к бесконечности. Цилиндрическая поверхность является частным случаем конической, когда вершина S удалена в бесконечность.
Определитель цилиндрической поверхности может иметь два вида:
Г (а, l), li a, li | | l
Г (a, s), li a, li S .
На рисунке показано задание цилиндрической поверхности и дискретного каркаса образующих.
На рисунке показано задание цилиндрической поверхности на ортогональном чертеже.
Если направляющая а является кривой 2-го порядка, то при движении образуется цилиндр 2-го порядка. Если направляющая а – ломаная, то образуется призматическая поверхность, которую можно считать частным случаем цилиндрической поверхности.
3.1.5. Линейчатая поверхность с плоскостью параллелизма
При формировании линейчатой поверхности с помощью плоскости параллелизма образующие должны быть параллельны этой плоскости поэтому они пересекаются с ней в несобственных точках, множество которых образуют несобственную прямую. Эту прямую следует рассматривать как третью направляющую линейчатой поверхности.
Определитель поверхности можно записать символически Q (а, b, Г), где а, b – направляющие, Г – плоскость параллелизма.
Закон движения образующих li a, li b, li | | Г. В зависимости от вида направляющих а и b поверхность с плоскостью параллелизма называется цилиндроидом, коноидом или косой плоскостью.
Цилиндроидом называется поверхность Каталана, у которой направляющие – кривые. Построить проекции каркаса образующих на ортогональном чертеже нетрудно, если плоскость параллелизма Г перпендикулярна плоскости проекций. В этом случае проекции прямолинейных образующих на одной плоскости проекций параллельны вырожденной проекции плоскости параллелизма, другие проекции образующих находят из условия их пересечения с направляющими а и b поверхностями.
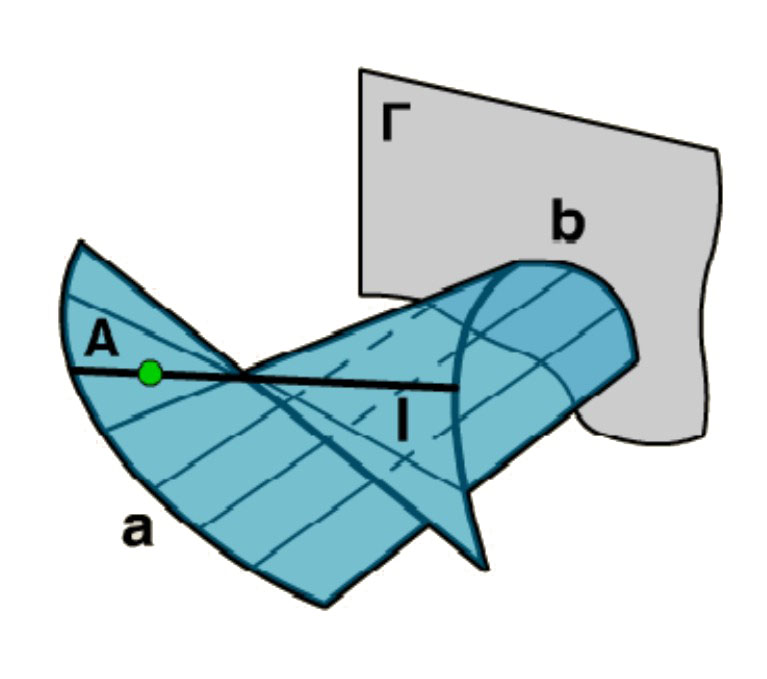
Построение фронтальной проекции А2 по заданной горизонтальной проекции А1 точки А принадлежащей цилиндру осуществлено проведением образующей l А.
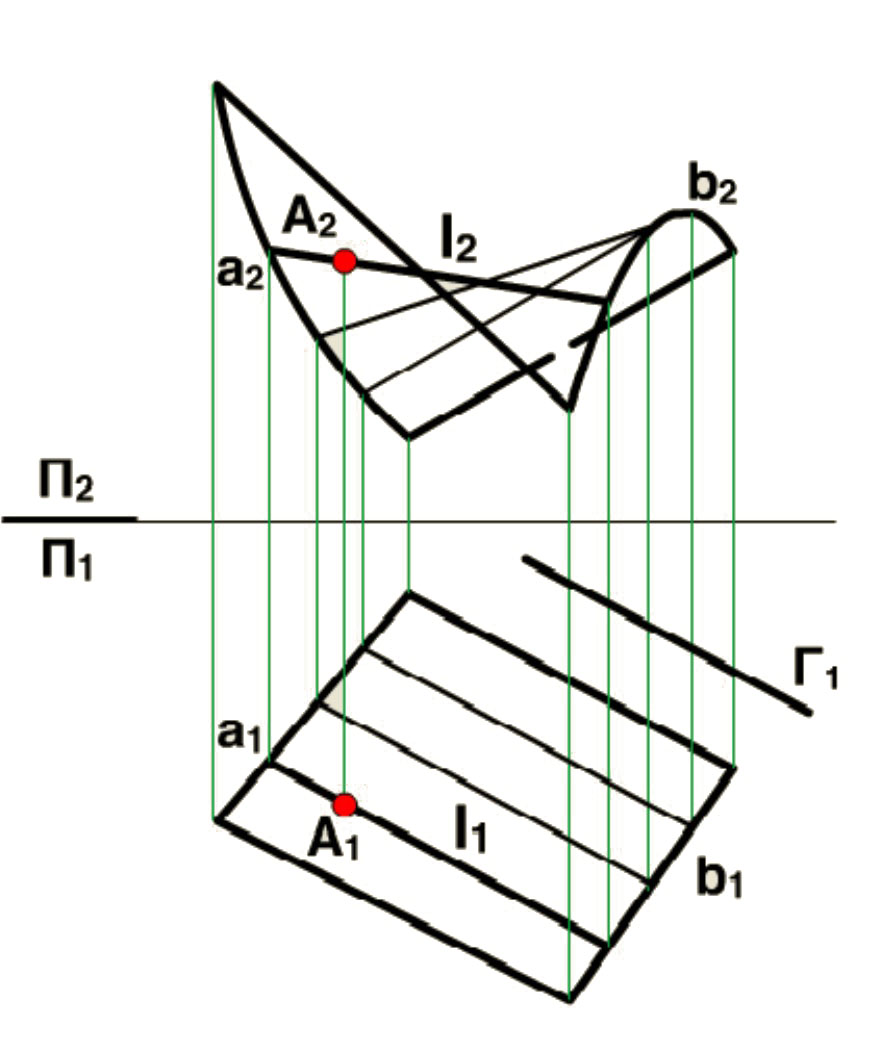
Коноидом называют линейчатую поверхность с плоскостью параллелизма, у которой одно направляющая – кривая, а другая – прямая. Плоскость параллелизма может быть параллельной П1 либо П2. В этом случае прямолинейные образующие являются горизонталями либо фронталями. На рисунке коноид задается аналогично цилиндроиду.
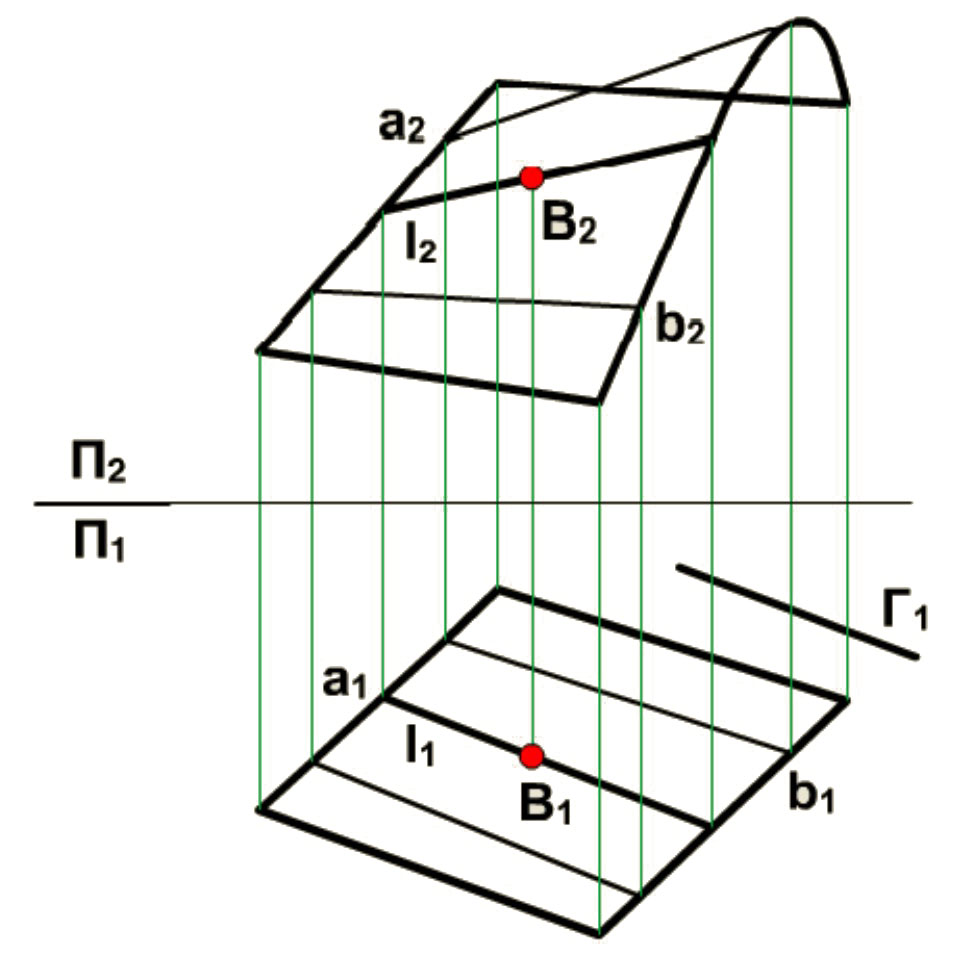
Косой плоскостью называется поверхность с плоскостью параллелизма, направляющими этой поверхности являются прямые а и b. Эта поверхность 2-го порядка, она имеет другое название – гиперболический пароболоид, т.к. несет на себе каркасы парабол и гипербол кроме того два каркаса прямоугольных образующих. На рисунке показано построение проекций прямолинейных образующих поверхности и проекции точки В, принадлежащих поверхностей.
