6.5 Розгортка поверхонь багатогранників
Розгорткою багатогранної поверхні називається плоска фігура, складена в певному порядку з граней багатогранника. При побудові розгорток багатогранників визначають дійсні величини всіх його граней. При цьому використовують різні способи перетворення епюра. Вибір способу залежить від виду багатогранника та його розміщення відносно площин проекцій.
Задача 1. Побудувати розгортку нижньої частини призми, зрізаної фронтально-проекційною площиною (рис.6.13).
На основі теоретичного матеріалу, описаного в попередньому підрозділі, знайдемо проекції перерізу прямої призми фронтально-проекційною площиною , а також побудуємо дійсну величину фігури перерізу способом суміщення, сумістивши площину з горизонтальною площиною проекцій.
Побудувати розгортку бічної поверхні прямої призми неважко, бо її горизонтально-проекційні ребра проеціюється на площину проекцій 2 у дійсну величину, а сторони нижньої основи зображаються на 1 також без спотворення довжини. Для того, щоб розгорнути призму, треба вибрати ребро, по якому уявно розріжемо призму для побудови розгортки бічної поверхні.
Як правило, вибирають те ребро, на якому знаходиться найнижча точка перерізу, або ж ребро, яке не зрізане. У даному випадку вибрано ребро АА′. Побудову розгортки починаємо з розгортки бокової поверхні. Для цього на горизонтальній прямій відкладаємо від обраної точки А0′ три відрізки, кожний з яких дорівнює довжині ребра основи призми. Через позначені точки проводимо вертикальні прямі і послідовно переносимо на них з вертикальної площини проекцій довжини бічних ребер нижньої зрізаної частини призми. Точки 10, 20, 30 сполучаємо ламаною лінією. Побудувавши розгортку бічної поверхні призми, до однієї з її ребер приєднуємо дійсну величину фігури перерізу і нижню основу. Побудову виконуємо методом засічок. Одержане зображення – повна розгортка нижньої зрізаної частини призми. Лінії зрізу і контур розгортки наводимо суцільною основною товстою лінією, а лінії згину – штрихпунктирною з двома крапками.
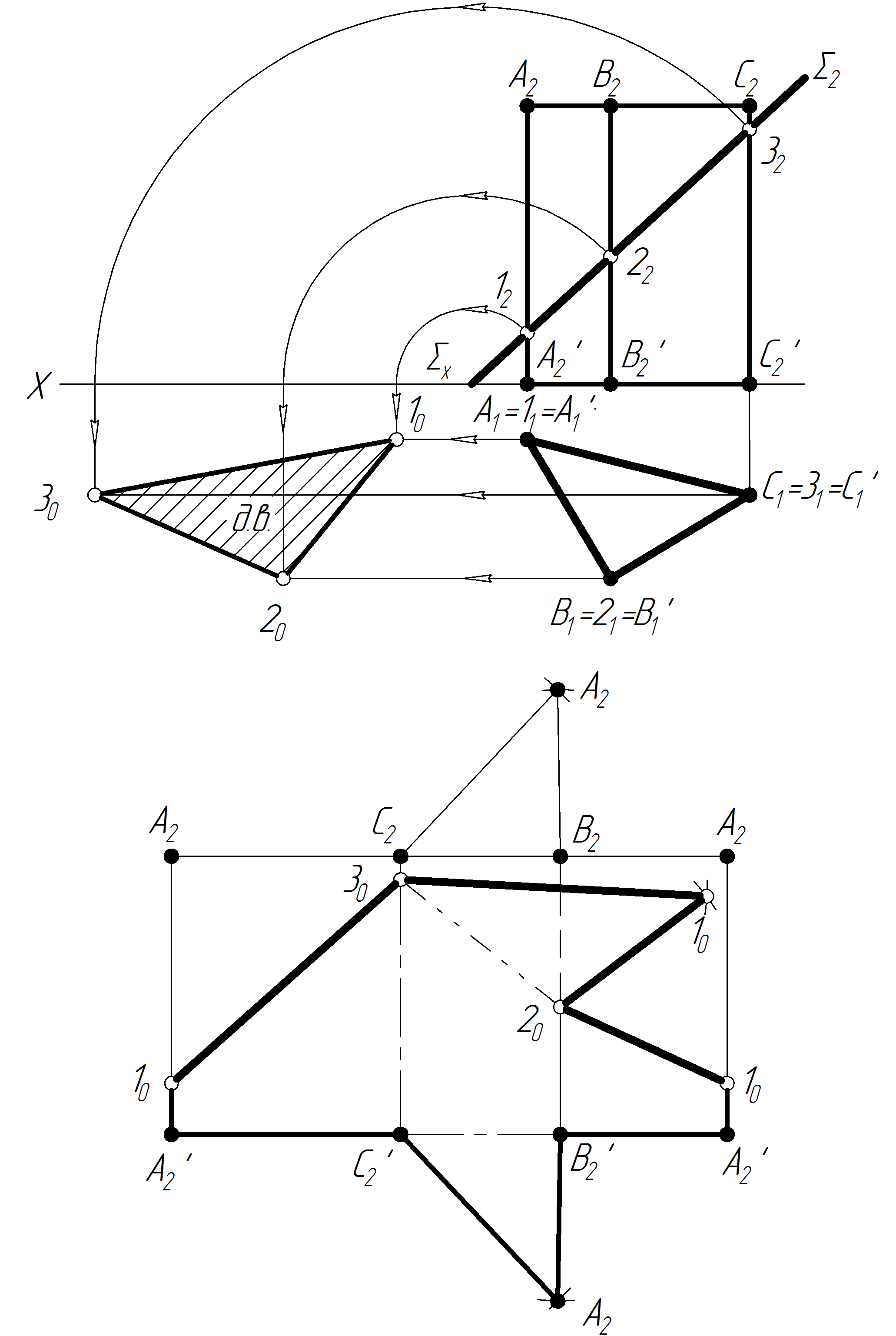
Рисунок 6.13
Задача 2. Побудувати розгортку нижньої частини піраміди, зрізаної фронтально-проекційною площиною (рис.6.14).
На основі теоретичного матеріалу, описаного, в підрозділі 6.4, знаходимо проекції перерізу прямої піраміди фронтально-проекційною площиною . Слід зауважити, що для знаходження точки 21 на профільному ребрі SB використаємо допоміжну горизонтальну площину α, проведену через точку 22. Площина α перетинає піраміду по трикутнику, подібному до трикутника основи піраміди. Вершина трикутника 2 і буде шуканою точкою. Побудову дійсної величини фігури перерізу знайдемо способом суміщення, сумістивши площину з горизонтальною площиною проекцій.
Розгортка бічної поверхні піраміди являє собою плоску фігуру, яка складається з трикутників – бічних граней піраміди. Щоб отримати повну розгортку піраміди, необхідно до розгортки бічної поверхні добудувати дійсну величину багатокутника основи. При побудові розгортки треба мати дійсну величину бокових ребер SA, SB, SC. Для цього ребро SC повернемо навколо осі, яка проходить через точку S перпендикулярно до площини проекцій 1, до положення, паралельного до площини проекцій 2 – S1C1′. На фронтальній проекції нове положення S2C2′ – це дійсна величина ребра SC. На цьому ребрі SC2′ – визначимо дійсну величину зрізаних ребер піраміди. Для цього з точок 12, 22, 32 проводимо горизонтальні лінії, які на відрізку SC2 відтинають S10, S20, S30, що є дійсними величинами зрізаних ребер піраміди.
Таким чином, всі необхідні елементи для побудови розгортки піраміди знайдено.
Спочатку будуємо розгортку бічної поверхні піраміди. Вона являє собою плоску фігуру, складену в певному порядку з трьох трикутників – дійсних величин бічних граней: S0А0=S0В0=S0С0=S2C2′.
Попередньо виберемо ребро SА (на якому знаходиться точка 1 – найнижча точка перерізу), по якому уявно розріжемо бокову поверхню піраміди. Виберемо довільну точку S0 на чистому полі місця креслення і методом засічок будуємо бокову розгортку піраміди. На кожному з ребер S0А0, S0В0, S0С0 відкладаємо точки 10, 20, 30, S210=S010 на ребрі SА, S220=S020 на ребрі SВ, S230=S030 на ребрі SС. Сполучимо точки А0, 10, 30, 20, 10, А0, В0, С0 прямими лініями, отримаємо розгортку зрізаної бічної поверхні піраміди.
Приєднавши до неї дійсні величини фігур основи і перерізу, побудованих методом засічок, дістанемо розгортку зрізаної (нижньої) частини поверхні піраміди.
Рисунок 6.14