6 Поверхні. Задання і зображення поверхонь
6.1 Загальні відомості
Поверхня – одне з основних геометричних понять. Кожна з поверхонь визначається, переважно, як геометричне місце точок у просторі, рівновіддалених від центра. У математиці поверхня розглядається як геометричне місце точок, які задовольняють певне алгебраїчне рівняння.
Будь-яка поверхня, як частина двовимірного простору, може бути утворена в результаті руху в просторі однієї лінії по іншій. Лінія, яка під час руху утворює дану поверхню, називається твірною, а лінія, по якій рухається твірна - напрямною. Твірна може змінювати положення, зберігаючи свою форму, або змінювати і положення і форму. Твірні і напрямні можуть бути як прямими, так і кривими лініями, що приводить до утворення великої кількості різноманітних поверхонь.
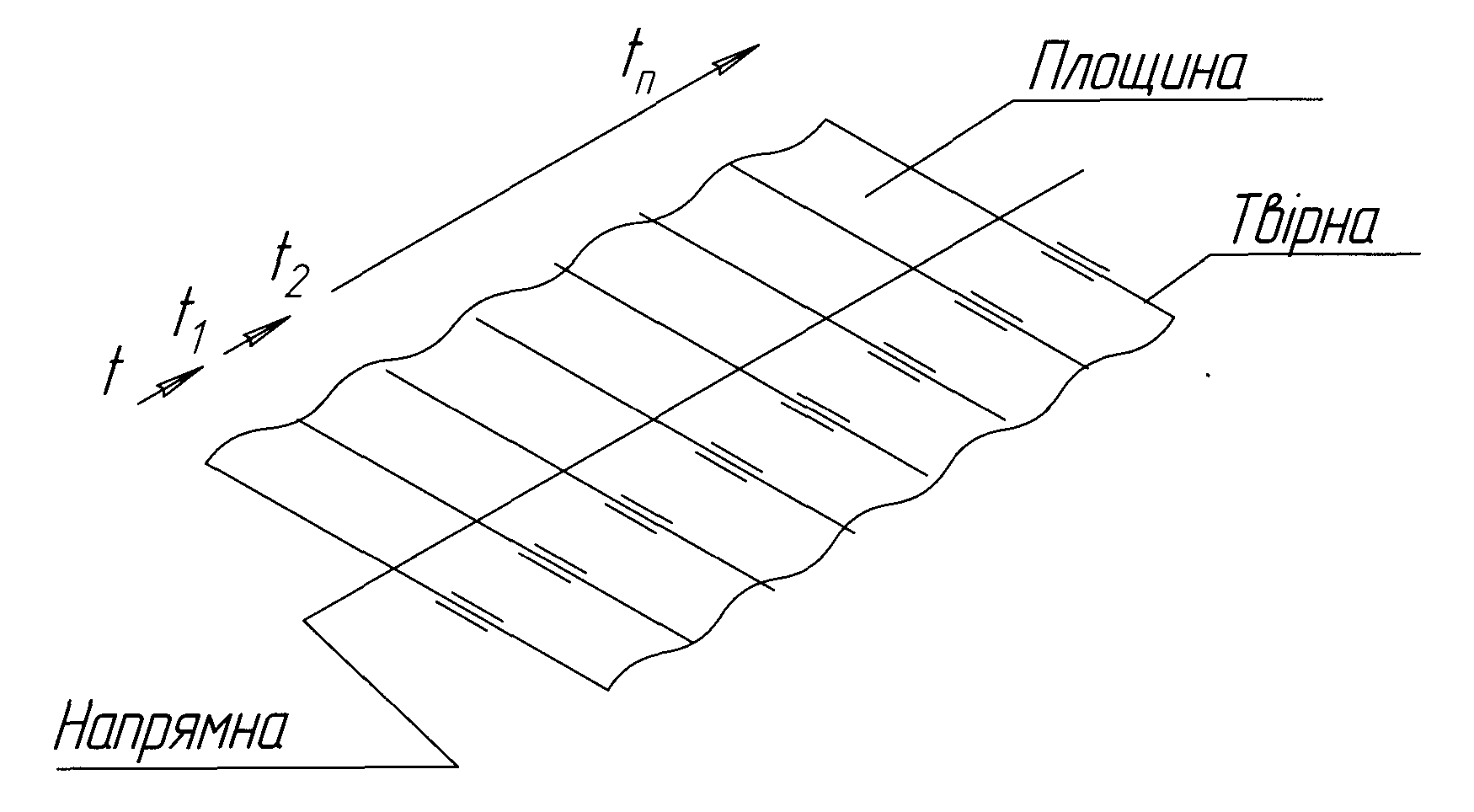
Рисунок 6.1
-- Утворення
площини
Найпростішою поверхнею є площина, яка утворюється ковзанням однієї прямої лінії по іншій прямій за умови, що під час руху твірна зберігає паралельність у всіх наступних положеннях до попереднього (рис.6.1). У даному випадку така умова є законом руху твірної по напрямній. Утворення поверхонь за такими правилами дає підставу називати такі поверхні кінематичними. Одна і та ж поверхня може бути утворена за різними правилами. Прикладом служить конус. Бічна поверхня прямого колового конуса може бути утворена :
обертанням навколо осі конуса закріпленої в точці S (вершина конуса) твірної t, яка ковзає по колу – напрямній (рис. 6.2);
рухом кола так, що його центр О рівномірно переміщається по прямій лінії – осі конуса від вершини до основи за умови, що одночасно з цим рухом радіус кола рівномірно змінюється (рис. 6.3).
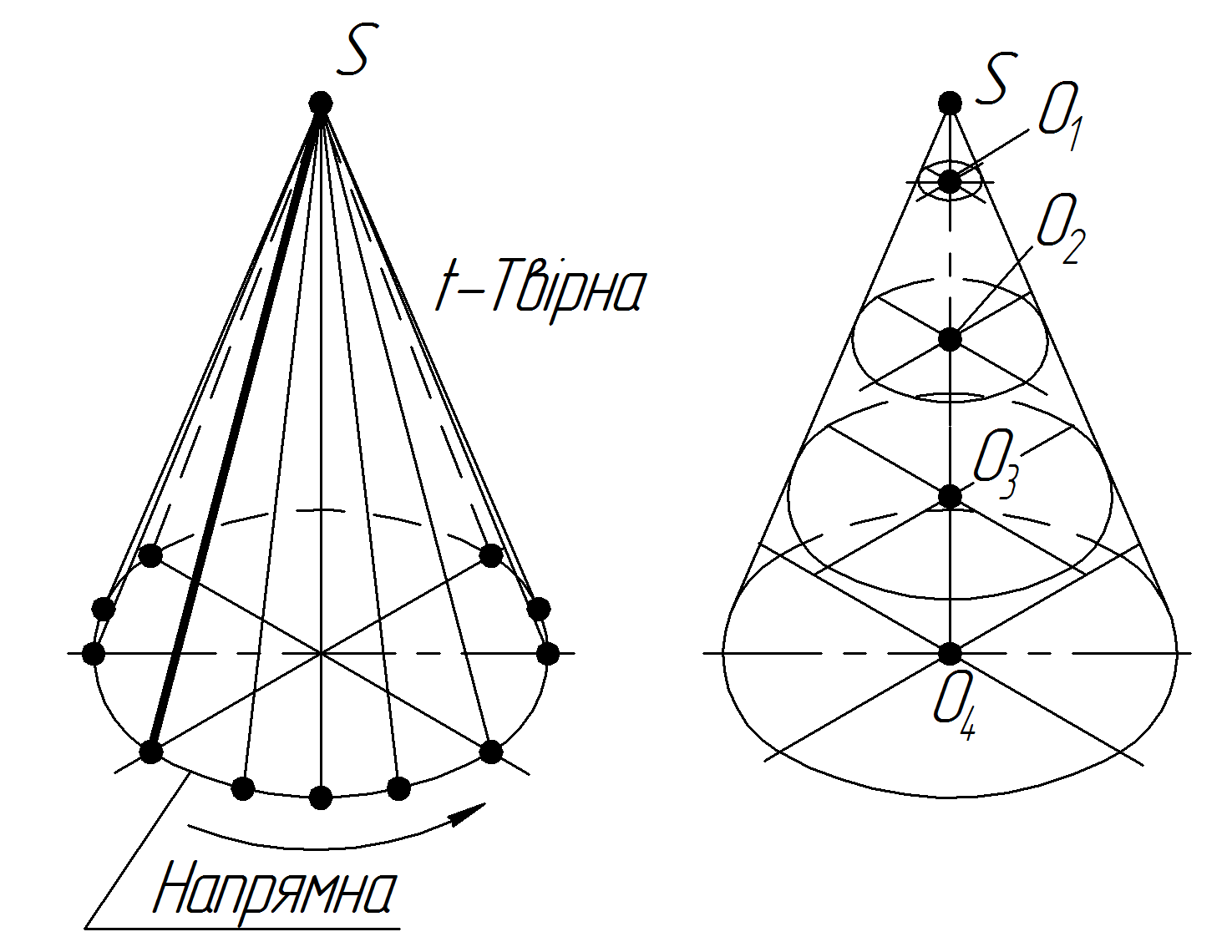
Рисунок 6.2
― Утворення
конуса
― Рисунок
6.3
Ламані твірні застосовують для утворення гранних поверхонь - пірамідальних і призматичних. Криві напрямні відповідають утворенню конічних, циліндричних і інших поверхонь .
Лінійчастими називають поверхні, твірною яких є пряма лінія.
Нелінійчастими (або кривими) поверхнями називають поверхні, які утворюються за допомогою твірних лише кривих ліній.
Поверхні діляться ще на розгортні і нерозгортні. До розгортних відносяться такі, які можна розгорнути без деформації – сумістити з площиною так, що всі елементи поверхні сумістяться в дійсній величині.
Нерозгортні поверхні при розгортці не можна сумістити з площиною. Прикладом служить сферична поверхня.
Поверхні також поділяються на закономірні, які описуються певними законами, і незакономірні (наприклад, земна поверхня). Найбільш загальне уявлення про поверхні дає наука топологія.
6.2 Багатогранні поверхні
Б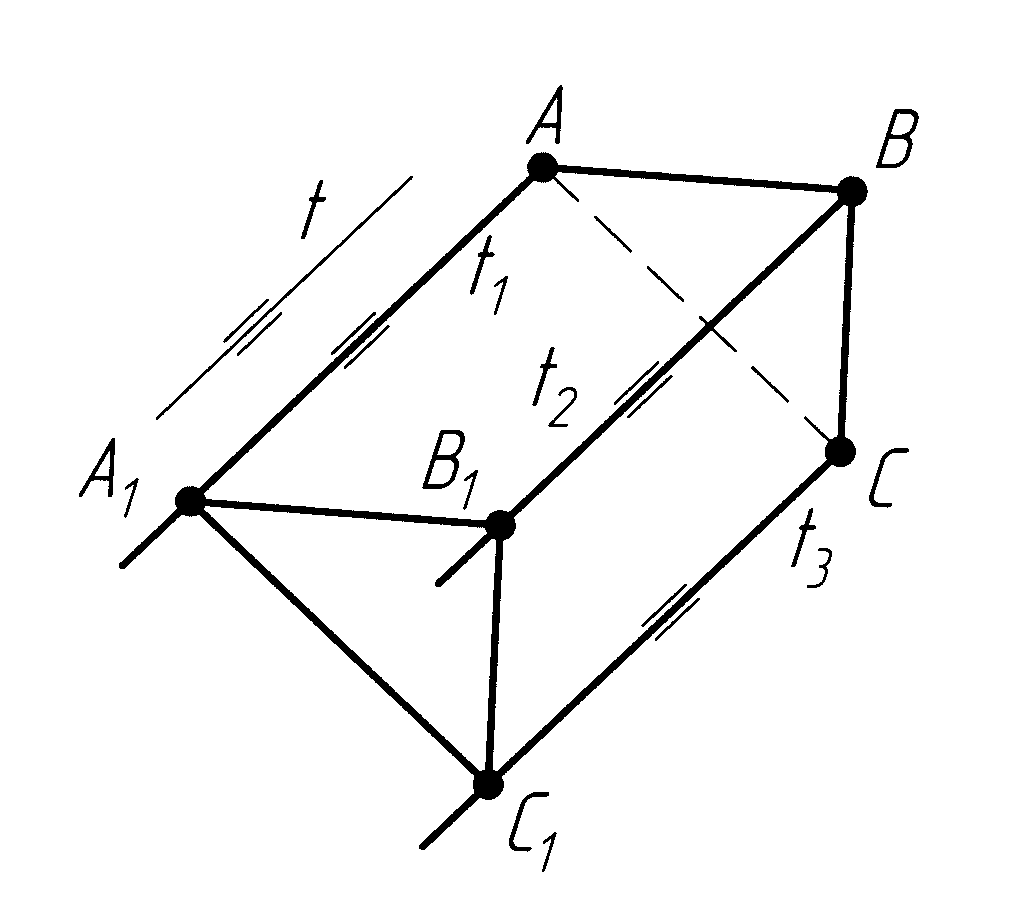
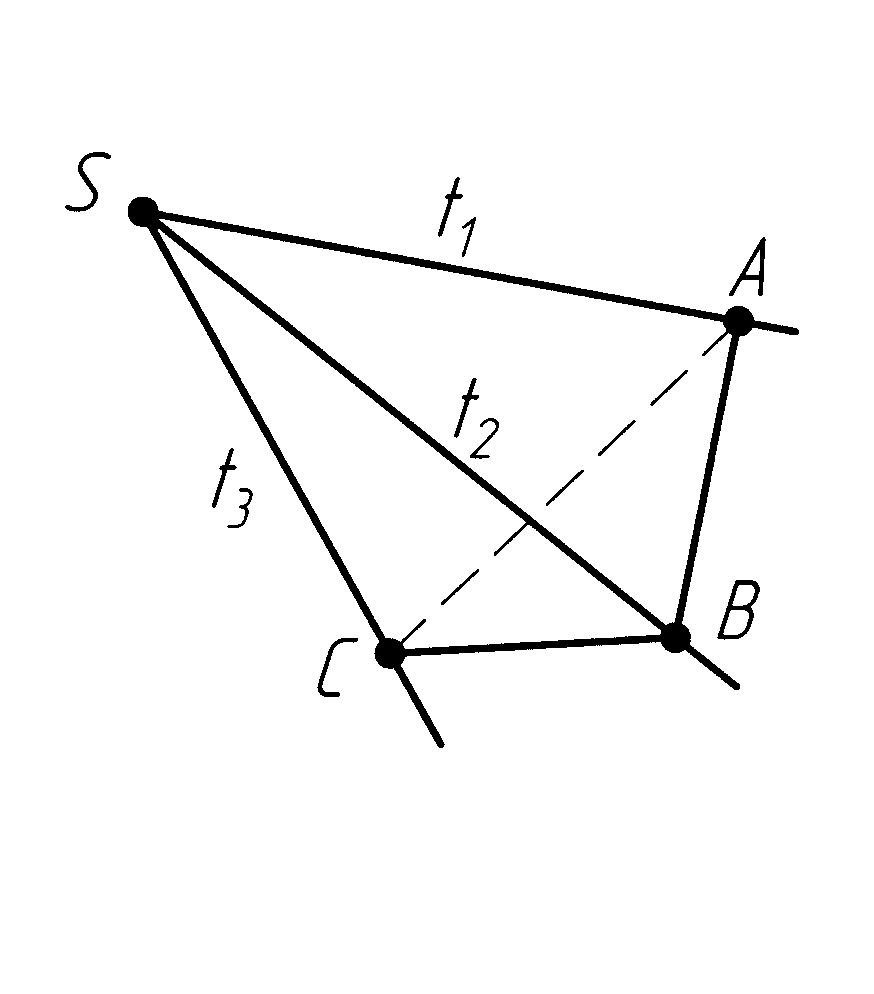агатогранником
називають частину простору, який обмежено
з усіх боків плоскими багатокутниками,
у яких кожна сторона одного з них є
одночасно стороною другого (але тільки
одного). Ці багатокутники називаються
гранями,
сторони їх – ребрами,
а їх вершини ─
вершинами багатогранника
(рис. 6.4).
Рисунок 6.4
– Утворення
багатогранників
Із різноманітності багатогранників найпоширенішими є призми (рис.6.5а,б) і піраміди (рис.6.5в,г).
Призмою називають багатогранник, дві грані якого є рівні багатокутники з відповідно паралельними сторонами. Ці багатокутники називаються основами. Якщо бокові ребра призми перпендикулярні до основи, то призму називають прямою призмою (рис. 6.5а), якщо бокові ребра не перпендикулярні до основи, то призма є похилою (рис. 6.5б). У прямої призми бокові грані – прямокутники. Якщо основою прямої призми є прямокутник, то призму називають паралелепіпедом.
Пірамідою називають багатогранник, одна грань якого - багатокутник (основа), а інші грані – трикутники, що мають спільну вершину. Якщо основою піраміди є правильний багатокутник і її висота проходить через центр цього багатокутника, то піраміду називають правильною (рис. 6.5в). Бокові грані правильної піраміди – рівні рівнобедрені трикутники. На рисунку 6.5г зображено похилу трикутну піраміду.
Багатогранники, у яких усі ребра, грані, плоскі, двогранні та просторові кути рівні між собою, називають правильними опуклими (тілами Платона).
Існують п’ять таких тіл:
а) тетраедр – чотиригранник, гранями якого є чотири рівносторонніх трикутники;
б) гексаедр - шестигранник або куб, гранями якого є шість квадратів;
в) октаедр – восьмигранник, гранями якого є вісім рівносторонніх трикутників;
г) додекаедр - дванадцятигранник, утворений із дванадцяти правильних п’ятикутників;
д) ікосаедр - двадцятигранник, утворений із двадцяти рівносторонніх трикутників.
Навколо всіх правильних багатогранників можна описати кулю.
а)
б)
в)
г)
Рисунок 6.5 – Прямі
та похилі багатогранники: