3.5 Взаємне положення двох прямих ліній

Прямі лінії у просторі можуть збігатися, перетинатися, бути паралельними і мимобіжними (рис. 3.12). Якщо однойменні проекції двох прямих а і b накладаються, то такі прямі в просторі збігаються.

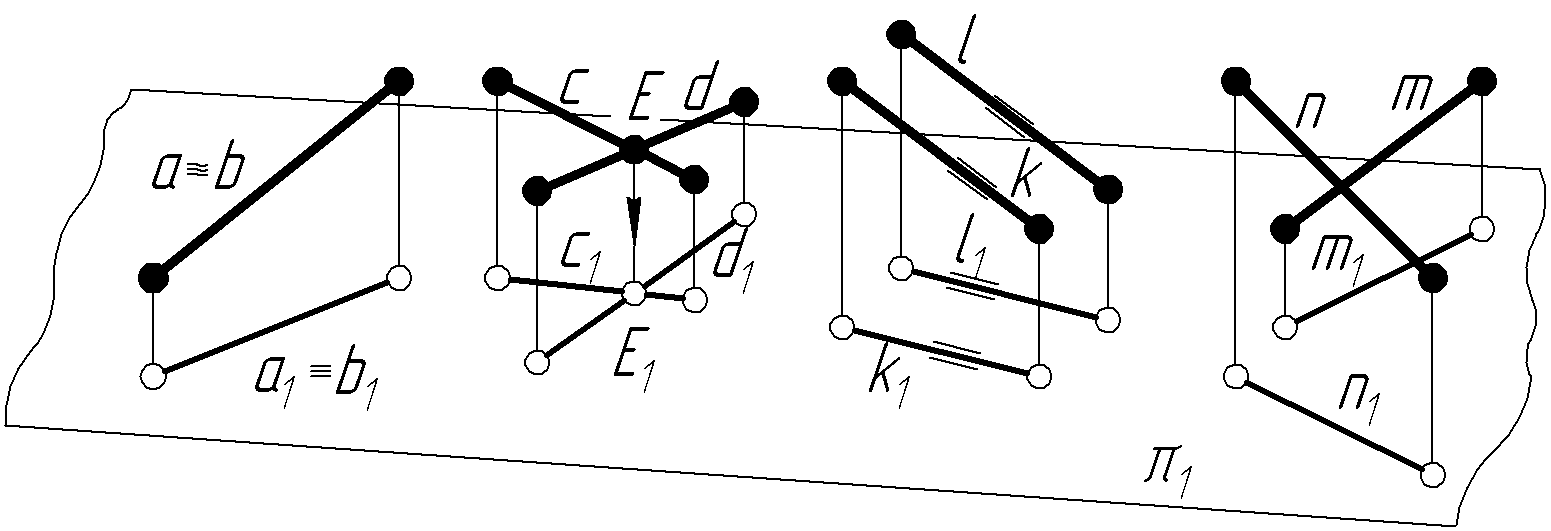
Рисунок 3.12 – Взаємне положення двох прямих ліній в просторі

Якщо дві прямі в просторі перетинаються (мають спільну точку), то на епюрі їх однойменні проекції перетинаються у точці, проекції якої лежать на одній лінії проекційного зв’язку (рис. 3.13а).

Якщо дві прямі довільного положення паралельні, то на епюрі їх однойменні проекції також паралельні (рис. 3.13б). Але, якщо прямі особливого положення паралельні до якоїсь із площин проекцій, то про положення прямих можна судити лише за наявністю їх проекцій на тій площині, до якої вони паралельні (рис. 3.13г, д) ─ прямі (рис.3.13г) та (рис.3.13д) не паралельні, бо профільні проекції їх відрізків не паралельні між собою.

Д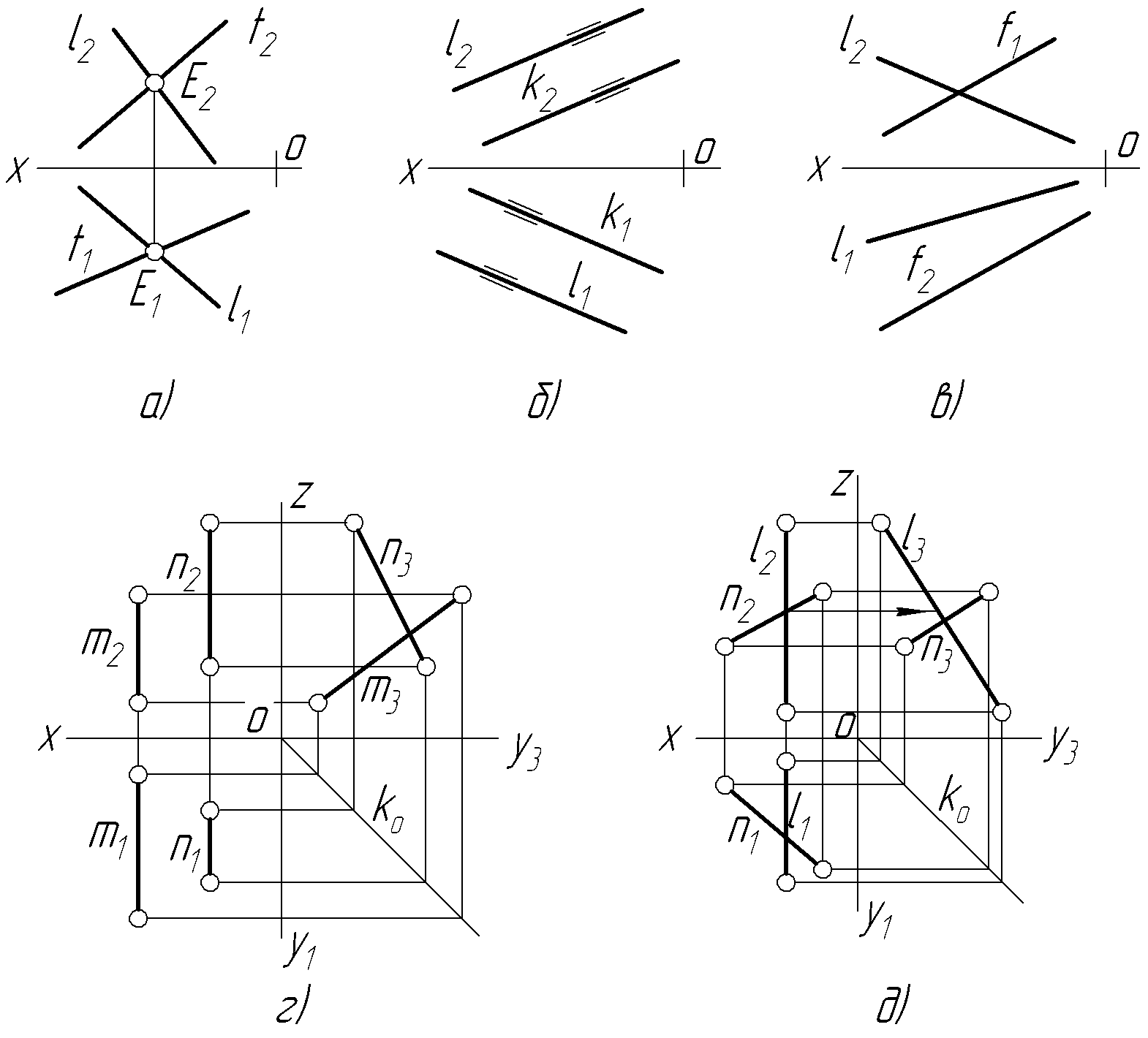 ві прямі, які у просторі не паралельні між собою і не перетинаються, називаються мимобіжними (рис. 3.13в, г, д). Для мимобіжних прямих характерно те, що їх однойменні проекції на епюрі перетинаються у точках, проекції яких не лежать на одній лінії зв’язку, наприклад, на одній площині проекцій проекції прямих перетинаються, а на другій можуть бути паралельними.

а)

б)

в)

г)

д)

Рисунок 3.13 – Відображення взаємного положення двох прямих ліній на епюрі

При побудові проекцій просторових фігур часто виникає необхідність встановити видимість двох точок, для яких дві координати однакові. Очевидно, що такі точки будуть розміщатися на одній проекційній прямій і їх відповідні проекції збігатимуться – ці точки

надалі будемо називати конкуруючими.

На рисунку 3.14а вершини А і В куба мають однакові координати X і Y і лежать на одній горизонтально-проекційній прямій, тому їх проекції А₁ і В₁ збігаються. З рисунка 3.14а видно, що точка А розміщена вище за точку В, оскільки координата Z точки А більша, тому при проеціюванні на горизонтальну площину проекцій (₁) точка А закриє точку В. Точка В – невидима.

Отже, робимо висновок, що із двох горизонтально-конкуруючих точок на горизонтальній площині проекцій буде видима та, яка розміщена в просторі вище ─ має більшу координату Z.

Міркуючи аналогічно і розглядаючи рисунок 3.14б, робимо висновок, що з двох фронтально-конкуруючих точок А і В на фронтальній площині проекцій видима та, що розміщена в просторі дальше від фронтальної площини проекцій ─ має більшу координату Y. Отже, на фронтальній площині точка А ─ видима, а точка В – невидима.

Надалі позначення проекцій невидимих (“закритих”) точок будемо брати в дужки.

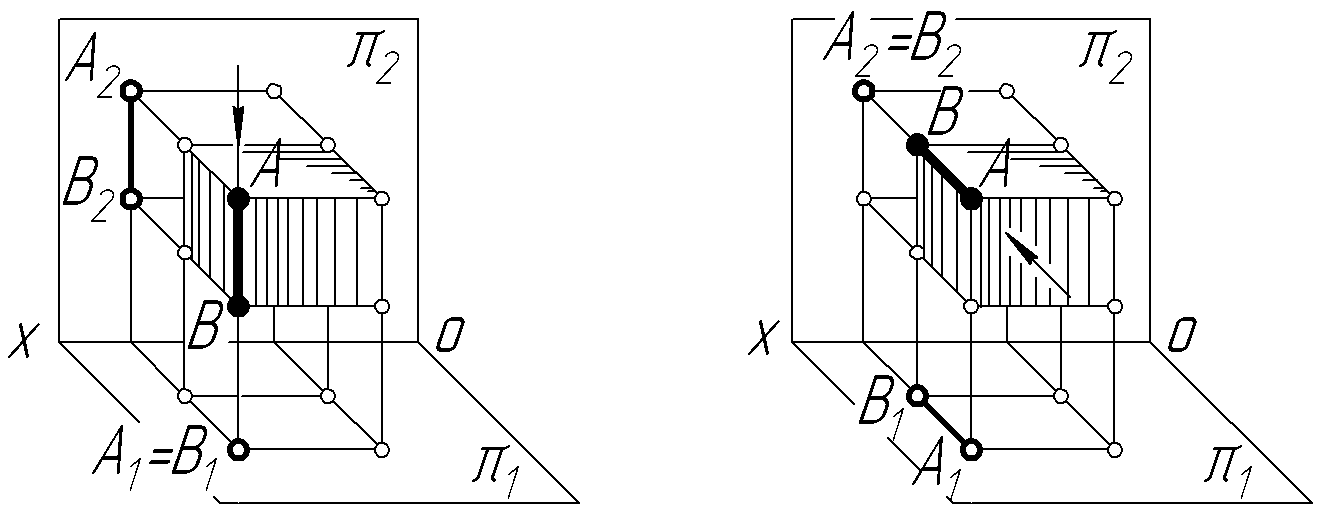
а)

б)

Рисунок 3.14 – Приклад знаходження конкуруючих точок на ребрах куба

На рисунку 3.15 точки А, В і С, D є точками уявного перетину двох мимобіжних прямих m і n. Справді, якщо подивитися на ці прямі зверху, то здається, що вони перетинаються в точці А₁≡В₁ (горизонтально-конкуруючі точки). Щоб переконатися, що ці прямі не перетинаються і яка пряма видима на П₁, треба побудувати фронтальні проекції точок А і В. Бачимо Z_А>Z_B. Отже, справедливий запис А₁≡(В₁). Міркуючи аналогічно, розглянемо точку С₂≡D₂ і побачимо, що Y_C >Y_D, отже справедливо С₂≡(D₂).

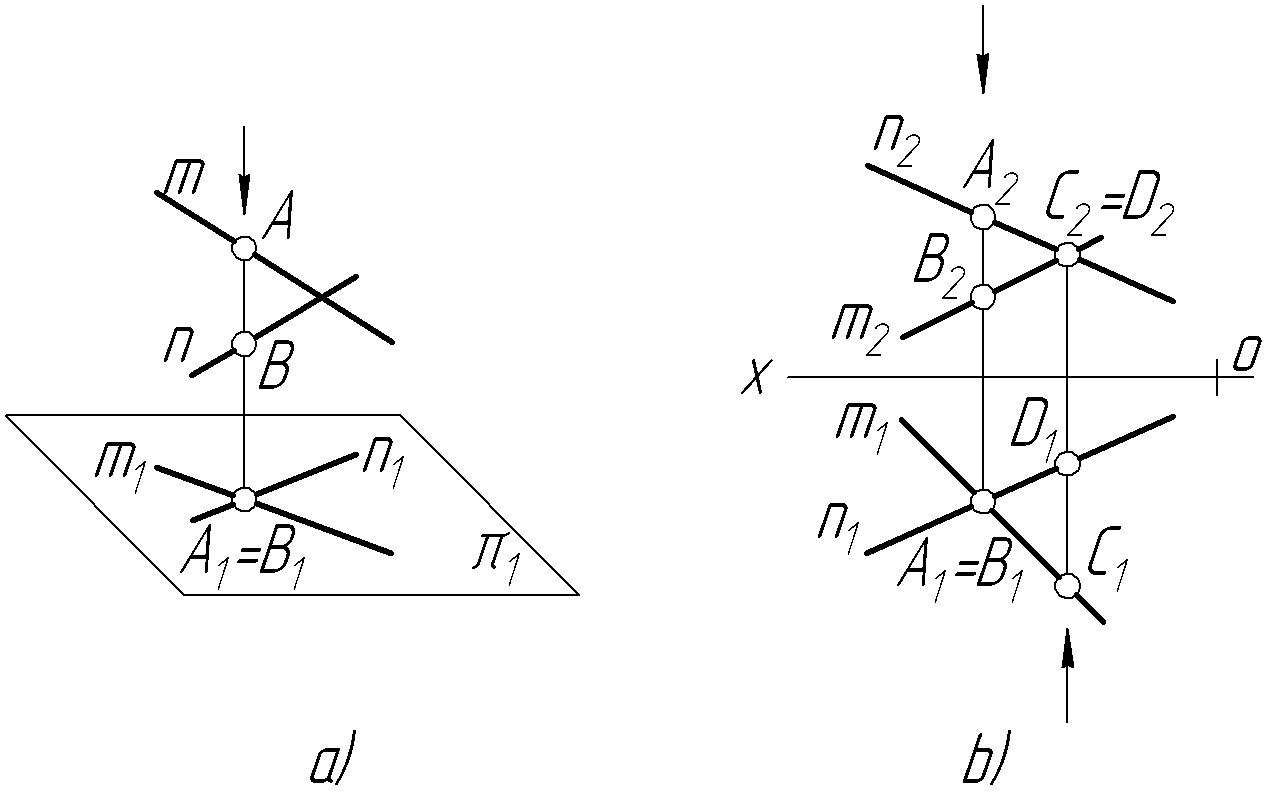
а)

б)

Рисунок 3.15 - Приклад знаходження конкуруючих точок на мимобіжних прямих