3 Пряма

Пряма в просторі визначається двома точками, які лежать на цій прямій. Побудувавши проекції цих точок і з’єднавши однойменні проекції між собою, одержимо проекції відрізка, що визначає задану пряму (рис. 3.1).

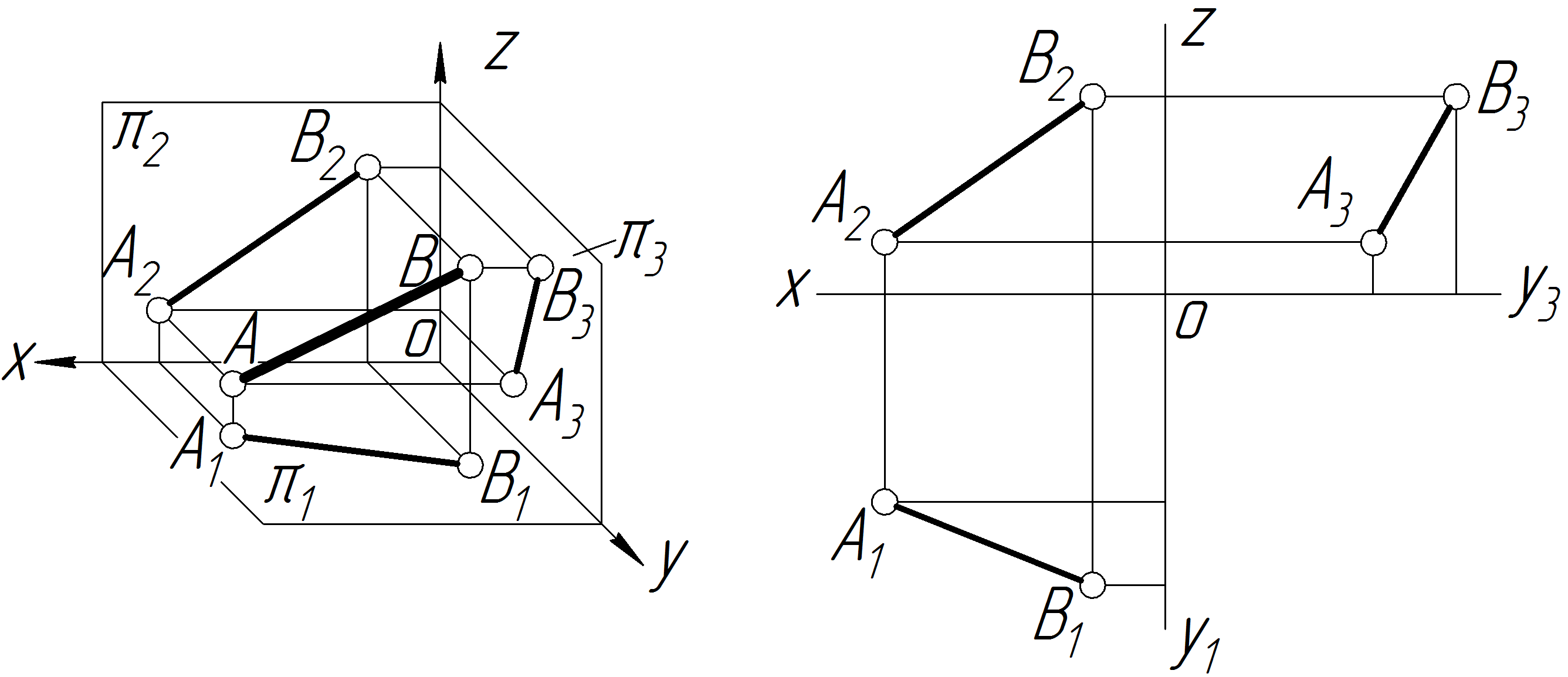
Рисунок 3.1 – Задання прямої на комплексному кресленні

3.1 Класифікація прямих

Положення прямої у просторі характеризується положенням її відносно площин проекцій. Відносно трьох площин проекцій ₁, ₂, ₃ пряма лінія може займати різні положення.

Довільним називається таке положення прямої, коли вона перетинає всі три площини проекцій під довільними кутами, тобто пряма не паралельна і не перпендикулярна до жодної з площин проекцій (рис.3.1).

Проекції відрізка довільного положення завжди менші, ніж відрізок у просторі. Жодна з проекцій такого відрізка не паралельна і не перпендикулярна до осей проекцій.

Усі інші положення прямої називають особливими.

Особливі прямі, які паралельні до однієї з площин проекцій, називають прямими рівня (табл.3.1).

Зокрема:

пряма, паралельна до площини ₂, ─ фронтальна;

пряма, паралельна до площини ₁, – горизонтальна;

пряма, паралельна до площини ₃, – профільна.

Для прямих рівня (табл. 3.1) характерним є те, що одна із проекцій відрізка, яким задана пряма, проектується в дійсну величину і саме на ту площину проекцій, до якої він паралельний.

Особливі прямі, які паралельні до двох площин проекцій і перпендикулярні до третьої площини проекцій, називають проеціюючими прямими (табл. 3.2).

Зокрема:

пряма, перпендикулярна до площини ₂, ─ фронтально-проекційна;

пряма перпендикулярна до площини ₁, – горизонтально-проекційна;

пряма перпендикулярна до площини ₃, – профільно-проекційна.

Для проеціюючих прямих (табл.3.2) характерним є те, що одна із проекцій відрізка, яким задана пряма, вироджується в точку і саме на ту площину проекцій, до якої він перпендикулярний.

Таблиця 3.1 – Прямі, паралельні до однієї з площин проекцій

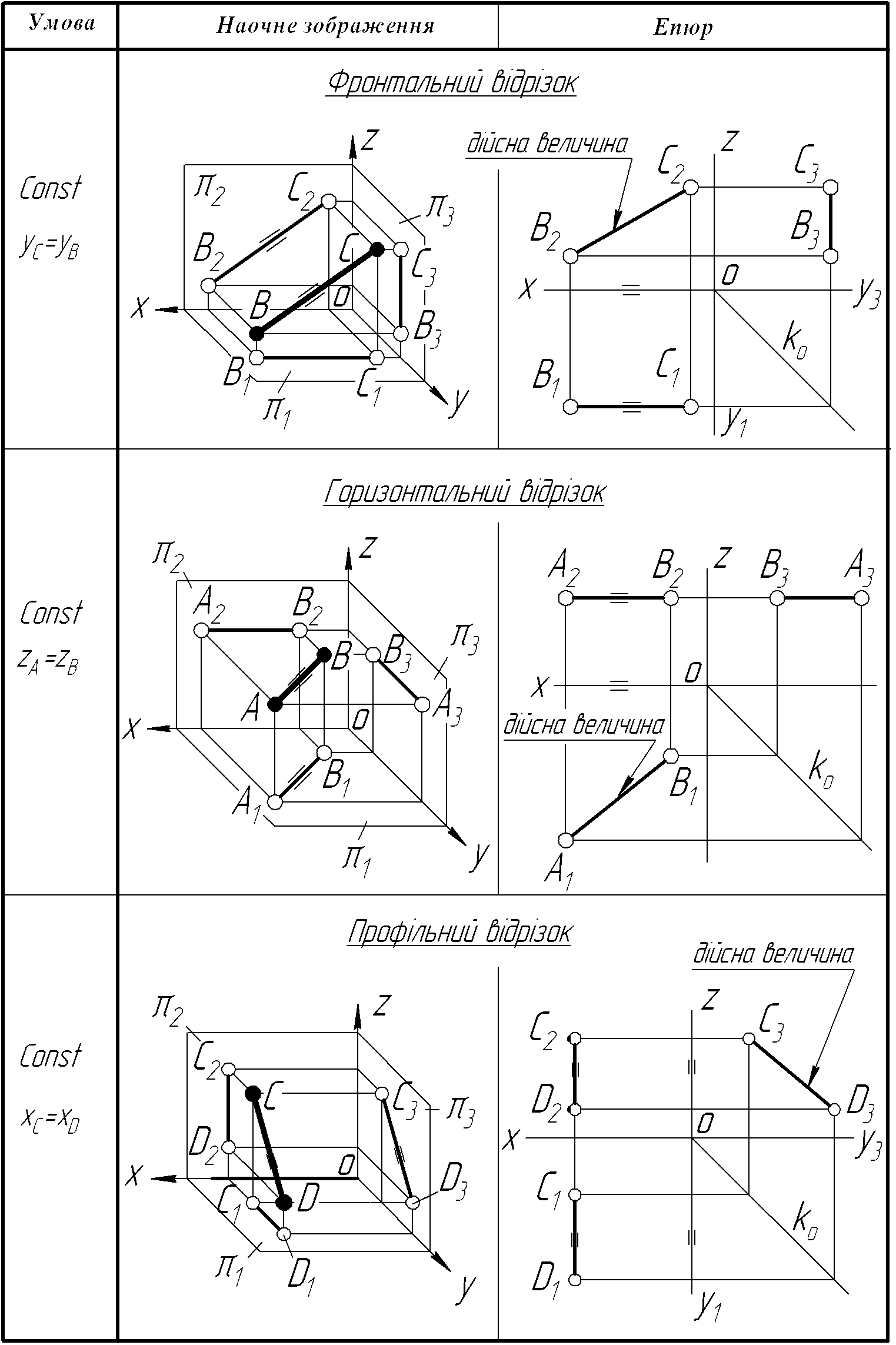
Таблиця 3.2 – Прямі, перпендикулярні до однієї з площин проекцій

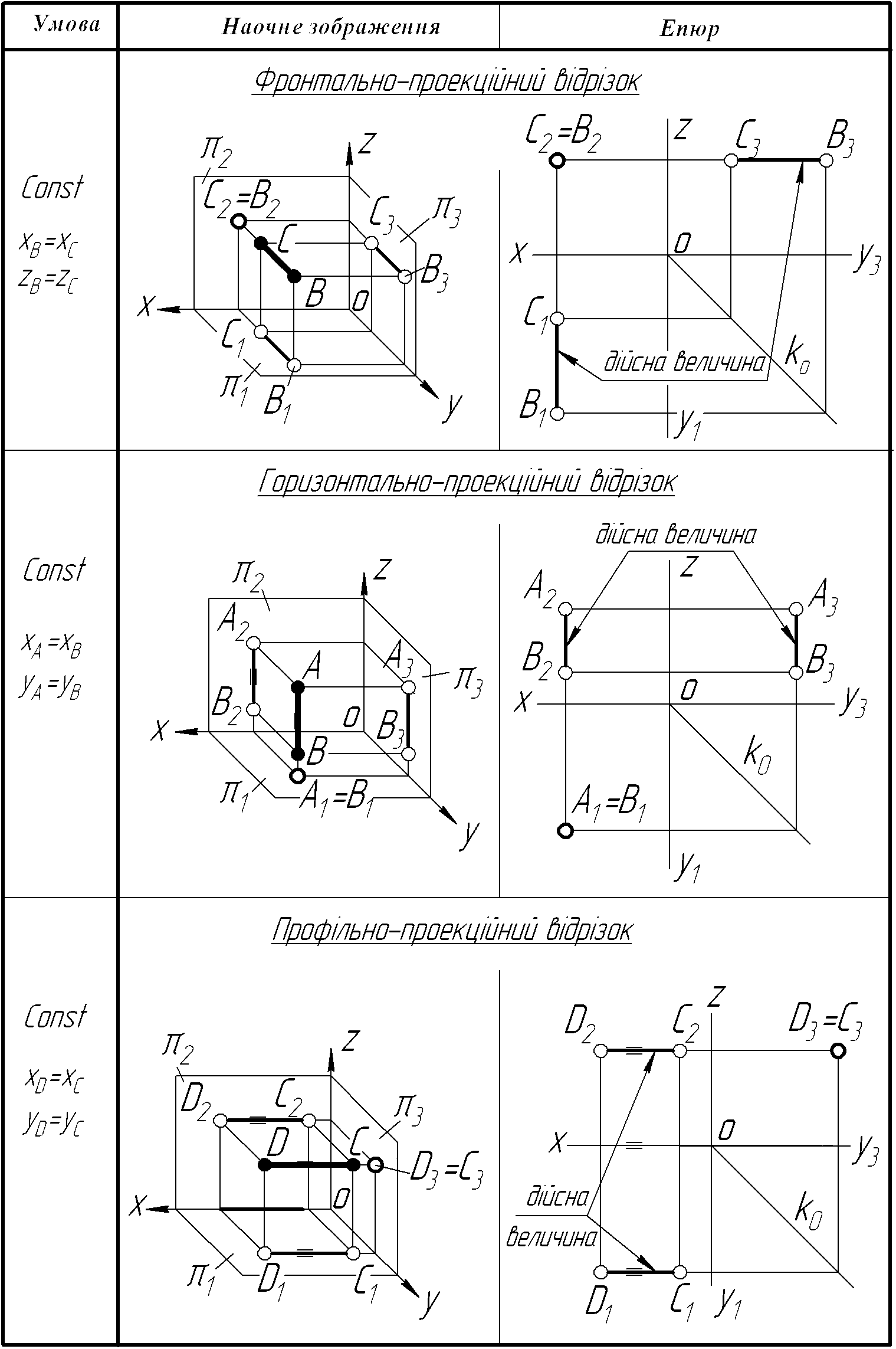
3.2 Точка на прямій. Поділ відрізка прямої у заданому співвідношенні

Якщо точка лежить на прямій, то на епюрі проекції точки лежать на однойменних проекціях цієї прямої.

Правильне також обернене твердження: якщо на епюрі проекції прямої проходять через однойменні проекції точки, то в просторі ця пряма проходить через точку.

З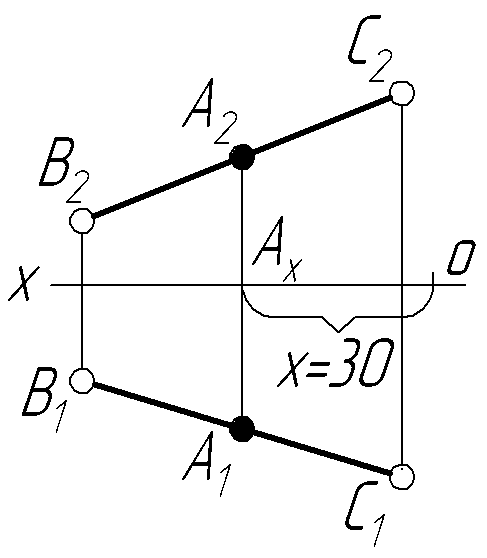 адача 1. На заданому відрізку ВС необхідно побудувати точку А, у якої координата Х = 30 мм (рис.3.2). Для цього по осі ОХ вліво від точки О відкладаємо відрізок ОА_Х = 30 мм. Через точку А_Х проводимо вертикальну лінію проекційного зв’язку до перетину з проекціями В₁С₁ і В₂С₂. Точки А₁ і А₂ – це проекції шуканої точки А.

С

Рисунок 3.2

пираючись на властивості паралельного проеціювання щодо співвідношення відрізків прямої та їх проекцій, виявляємо, що для поділу відрізка прямої в заданому пропорційному співвідношенні досить поділити у цьому співвідношенні одну з проекцій відрізка, а потім за допомогою ліній зв’язку перенести точки поділу на інші проекції відрізка.

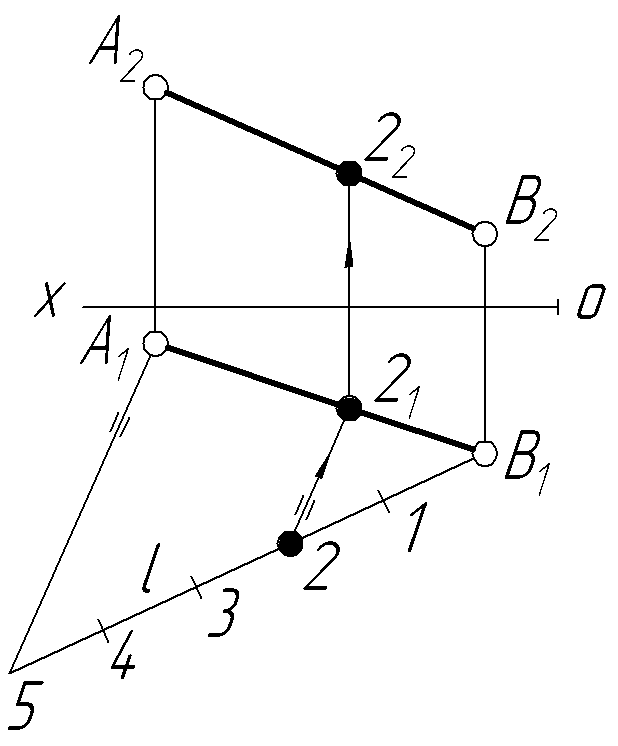
Задача 2. На рисунку 3.3 треба поділити відрізок АВ у співвідношенні 2:3, починаючи з точки В.

Н

Рисунок 3.3

асамперед поділимо горизонтальну проекцію відрізка А₁В₁ у заданому співвідношенні. Для цього з точки В₁ під гострим кутом до А₁В₁ проводимо довільну пряму l, на якій відкладаємо від точки В₁ п’ять (5=3+2) рівних відрізків довільної довжини. Точку 5 з’єднуємо з другим кінцем відрізка - точкою А₁. Точка 2, яка ділить відрізок В₁5 у співвідношенні 2:3, переносимо на проекції відрізка АВ (показано стрілками). Відрізок 22₁ проходить паралельно відрізку 5А₁.