4.2 Пряма і точка в площині

Пряма може належати площині, бути паралельною до площини і перетинати площину. Точка може належати площині або ж не належати площині.

Розглянемо умови належності прямої і точки до площини:

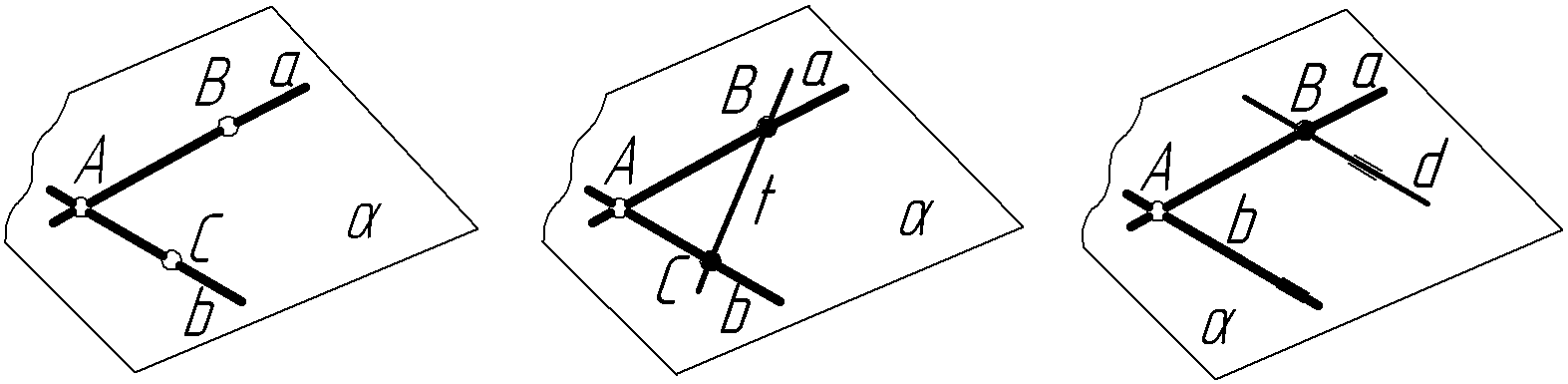
• Точка належить площині, якщо вона лежить на прямій, яка належить цій площині. На рисунку 4.4а площина  задана двома прямими а і b, що перетинаються в точці А. Точки В і С належать цій площині  також, бо лежать, відповідно, на прямих а і b, що задають площину. Отже, щоб побудувати довільну точку, яка б лежала у площині, необхідно в даній площині провести пряму і на цій прямій вибрати довільну точку.

• Пряма належить площині, якщо вона проходить через дві точки, які належать цій площині. На рисунку 4.4б пряма t, яка з’єднує точки В і С, належить цій площині . Отже, щоб побудувати пряму, що лежить у площині, необхідно задати дві точки, які належать площині, і через ці точки провести пряму, яка і буде належати даній площині.

• Пряма належить площині, якщо вона проходить через точку, яка лежить у площині і проходить паралельно прямій, що лежить у цій площині. На рисунку 4.4в пряма d, яка проходить через точку В, що належить площині , є паралельною до прямої в, що лежить у площині , і буде прямою, яка належить площині .

а)

в)

б)

Рисунок 4.4 – Належність точки та прямої до площини

У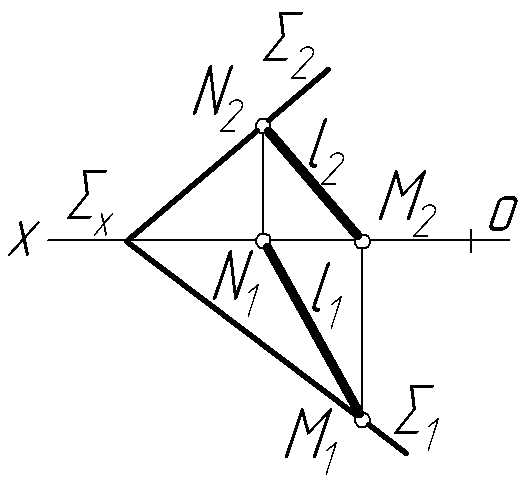 нарисній геометрії правдиве твердження, що пряма належить площині, якщо її сліди лежать на однойменних слідах площини (рис. 4.5).

О

Рисунок 4.5 – Належність прямої до площини

тже, щоб провести пряму, яка лежить у даній площині, необхідно задати точку в площині і через цю точку провести пряму, яка паралельна до будь-якої прямої даної площини (в тому числі і одному із слідів даної площини). Якщо точка або пряма лежить у площині особливого положення, то необхідно керуватись збираючою властивістю проекційних площин (підрозділ 4.1) і не проводити попередніх побудов.

Задача 1. Через відрізок АВ провести горизонтально-проекційну площину  (рис.4.6а).

В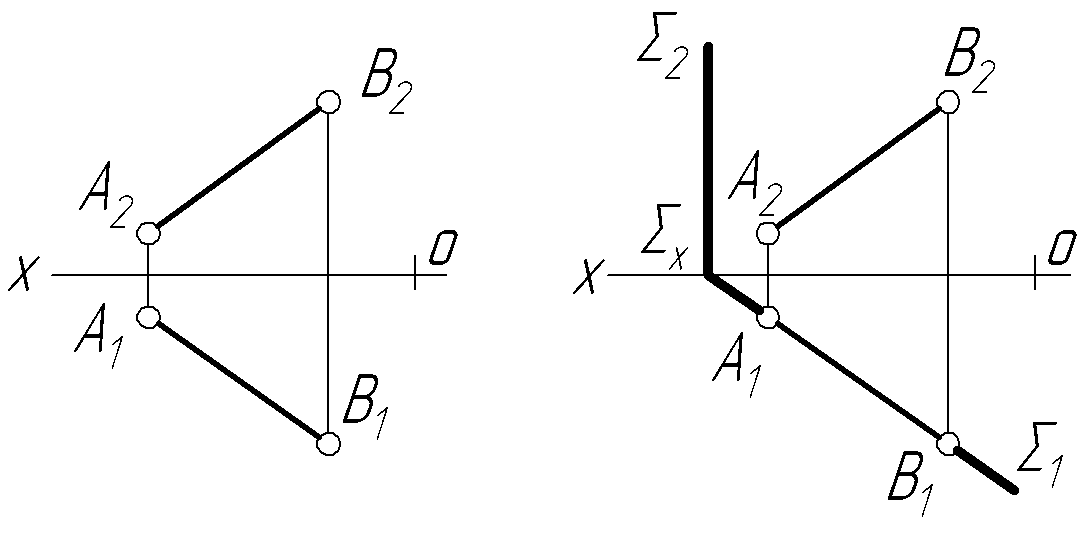 икористовуючи збираючу властивість проекційних площин, розуміємо, що горизонтальний слід площини збігається з горизонтальною проекцією прямої АВ. Продовжимо А₁В₁ до перетину з віссю ОХ і знайдемо _Х ─ точку збігу слідів площини  на осі ОХ, і через неї проведемо фронтальний слід площини ₂, який пройде перпендикулярно до осі ОХ, що властиво всім горизонтально-проекційним площинам. Отже, горизонтально-проекційну площину побудовано і відрізок АВ належить їй (рис. 4.6б).

а)

б)

Рисунок 4.6

Задача 2. Побудувати відсутні проекції точок, якщо відомо, що точки А, В, С належать горизонтальній площині, заданій трикутником АВС. Визначити відстань площини трикутника АВС до площини проекцій, якій вона паралельна (рис.4.7а).

Відомо з попереднього матеріалу, що горизонтальна площина на площинах проекцій має фронтальний слід, розміщений паралельно до осі ОХ, і що все, що лежить у цій площині, “збирається” фронтальним слідом. Тому через А₂ паралельно до осі ОХ проводимо ₂ ─ фронтальний слід горизонтальної площини (рис. 4.7б). Цей слід “збирає” на себе фронтальні проекції точок В і С. Координата Z і є відстанню від площини  до ₁ (рис.4.7в).

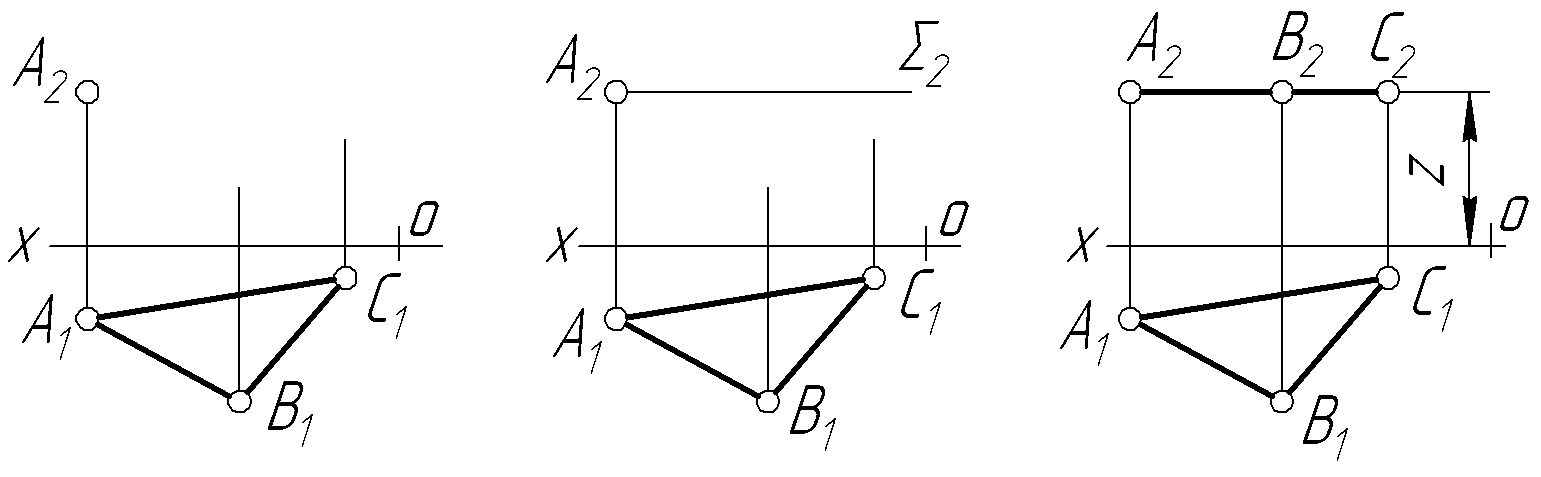
а)

б)

в)

Рисунок 4.7