4 Площина
4.1 Способи задання площини та класифікація площин
Н
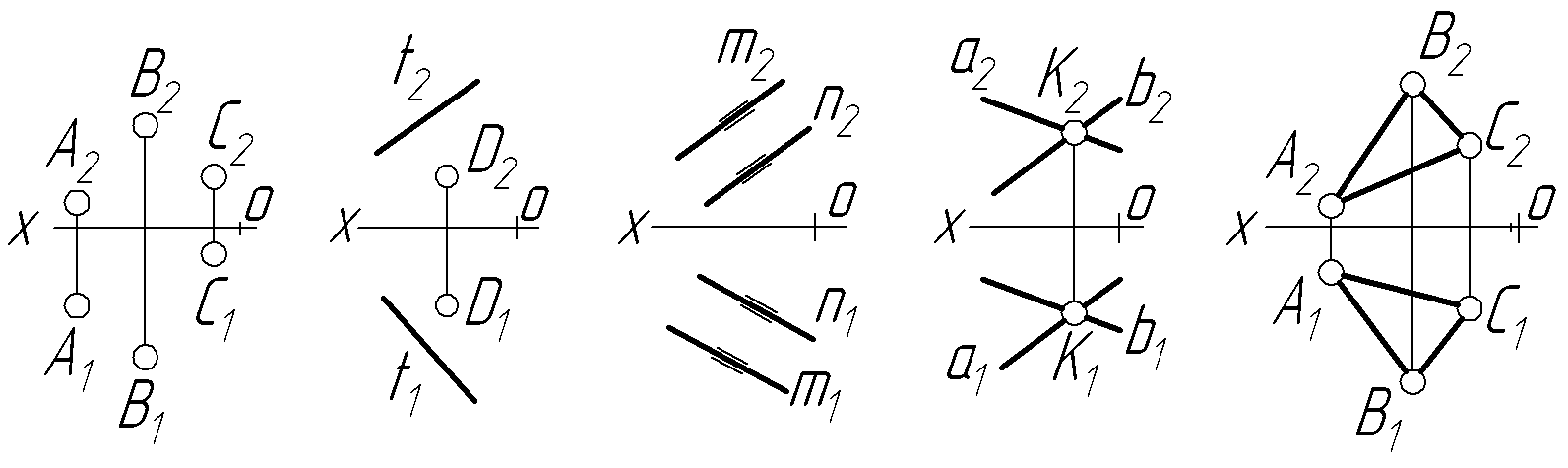а
епюрі площина задається проекціями
трьох точок, що не лежать на одній прямій,
проекціями прямої і точки, яка лежить
поза нею, проекціями паралельних прямих,
проекціями прямих, що перетинаються,
плоскою фігурою (рис.4.1).
Рисунок 4.1 – Задання площини на
епюрі
П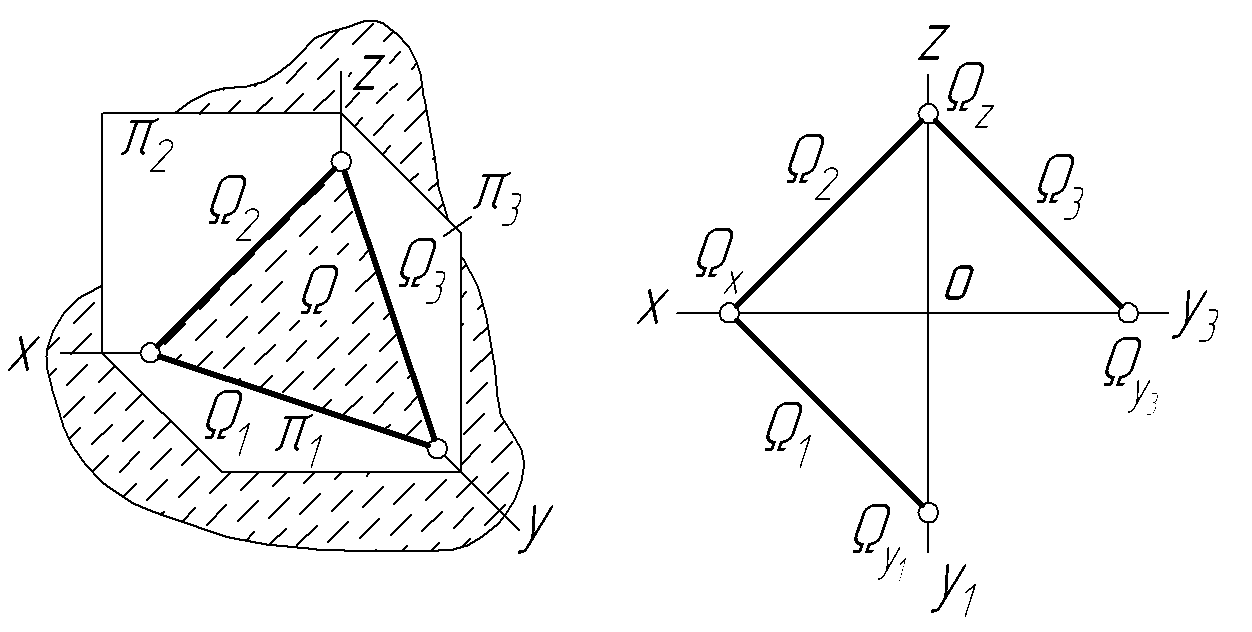
лощину
на епюрі можна задати ще слідами. Це,
фактично, метод задання двома прямими,
що перетинаються, до того ж, це прямі
особливого положення, оскільки вони
лежать на площинах проекцій.
Рисунок 4.2 – Площина загального положення
Слідом площини називають пряму лінію, по якій площина перетинається з площиною проекцій.
Точкою збігу слідів називають точку перетину площини з віссю проекцій. Це точка на площині з однією координатою, бо дві інші дорівнюють нулю. Положення площин у просторі характеризуються їх розміщенням відносно площин проекцій. У зв’язку з цим розрізняють площини довільного положення і особливого.
Площина довільного (або загального) положення – це площина, не перпендикулярна і не паралельна жодній із площин проекцій (рис. 4.2).
Площина проекційна – це площина, яка перпендикулярна до однієї з трьох площин проекцій і не паралельна до двох інших.
Площина, перпендикулярна до 1, – горизонтально-проекційна.
Площина, перпендикулярна до 2, – фронтально-проекційна.
Площина, перпендикулярна до 3, – профільно-проекційна.
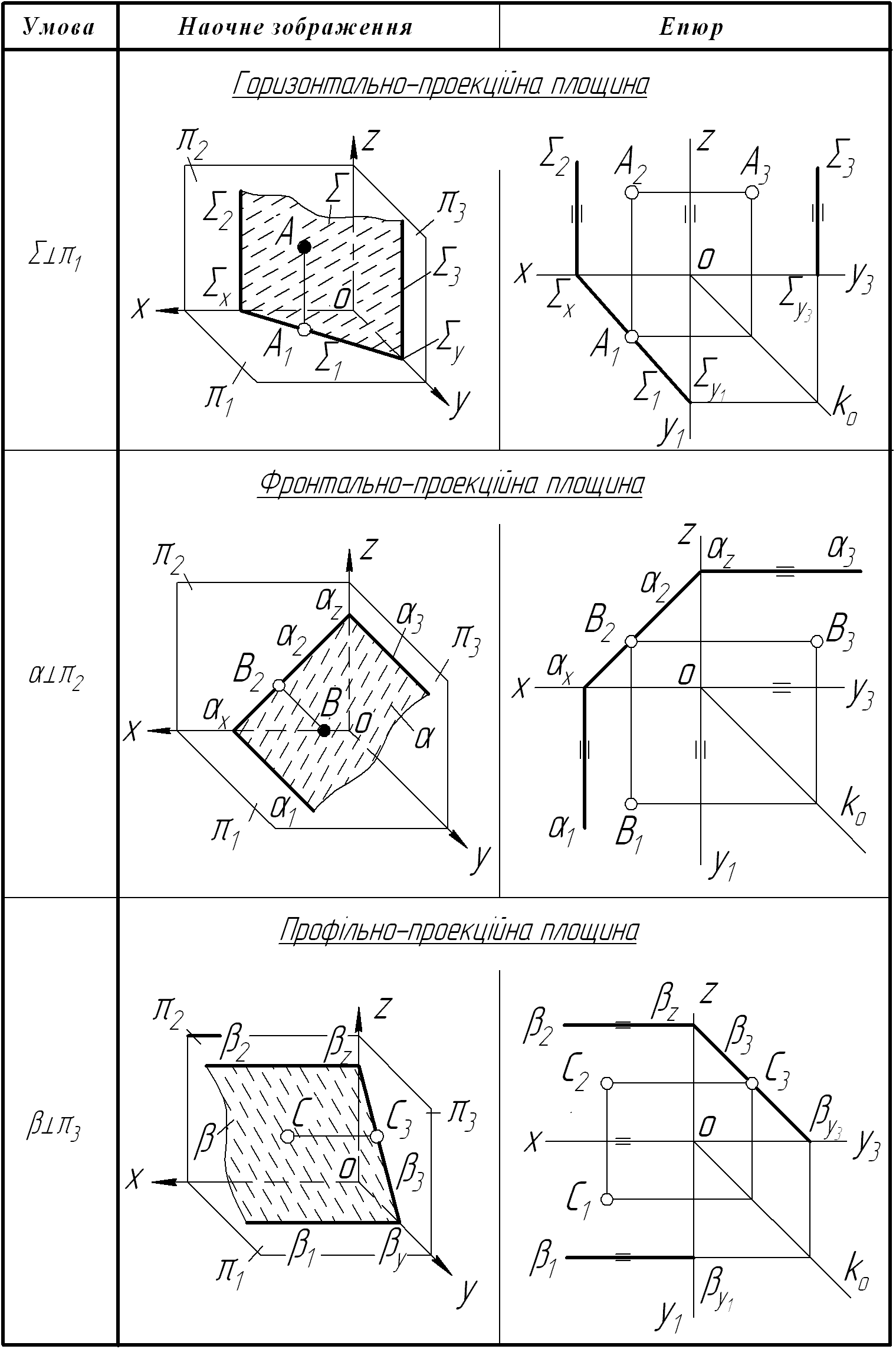
Всі вище названі площини зображені в таблиці 4.1.
Назва площини вказує на те, до якої площини проекцій дана площина перпендикулярна. У випадку проекційної площини всі точки, криві та прямі лінії, плоскі фігури, які лежатимуть у цій площині, збігатимуться з одним із слідів площини, і саме зі слідом на площині проекцій, до якої ця проекційна площина перпендикулярна. Другий слід завжди буде перпендикулярний до осі проекцій.
Такий збіг сліду площини з усіма елементами, що лежать у ній, називають збираючою властивістю.
Проекційні площини в системі трьох площин проекцій мають три сліди.
Таблиця 4.1 – Проекційні площини
На рисунку 4.3 зображена профільно-проекційна осьова площина ─ тобто площина, яка проходить через вісь ОХ. Ця площина може бути бісекторною, якщо вона ділить просторовий кут між 1 і 2 на дві рівні частини. Така площина характерна тим, що вона є геометричним місцем точок, рівновіддалених від фронтальної (2) і горизонтальної (1) площин проекцій. Отже, будь-яка точка цієї площини має однакові координати Z і Y. Фронтальний і горизонтальний сліди таких площин збігаються з віссю ОХ.
У системі двох площин проекцій 2 і 1 осьова площина може задаватися точкою і слідами, які збігаються з віссю ОХ (рис. 4.3).
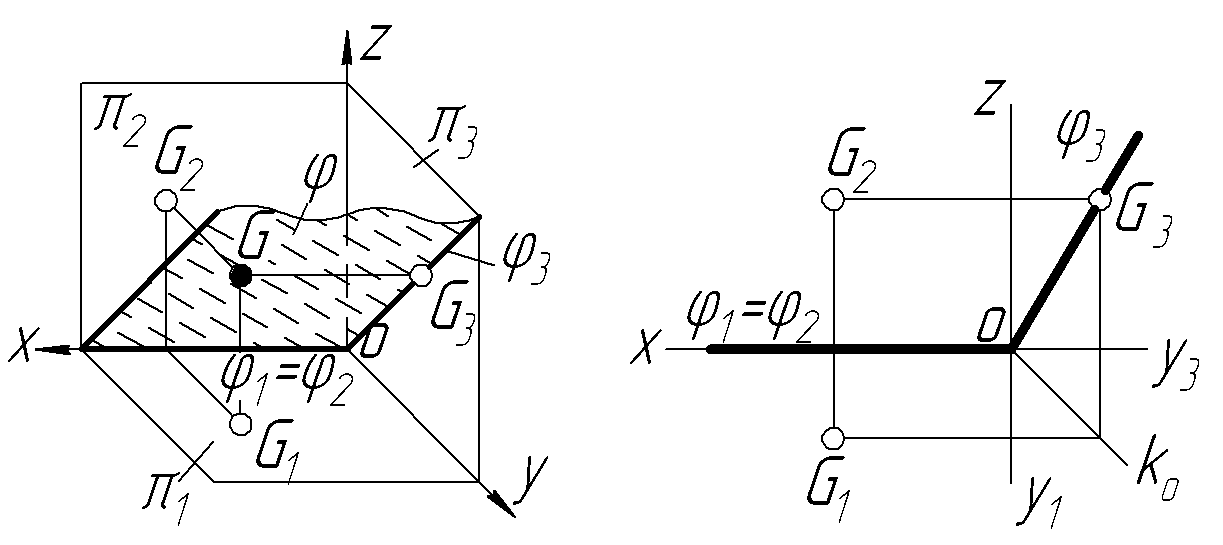
Рисунок 4.3 – Осьова площина
Двічі проекційною (або площиною рівня) називають площину, яка паралельна до однієї із площин проекцій і перпендикулярна до двох інших площин проекцій. Такі площини зображені у таблиці 4.2.
Таблиця 4.2 – Двічі проекційні площини
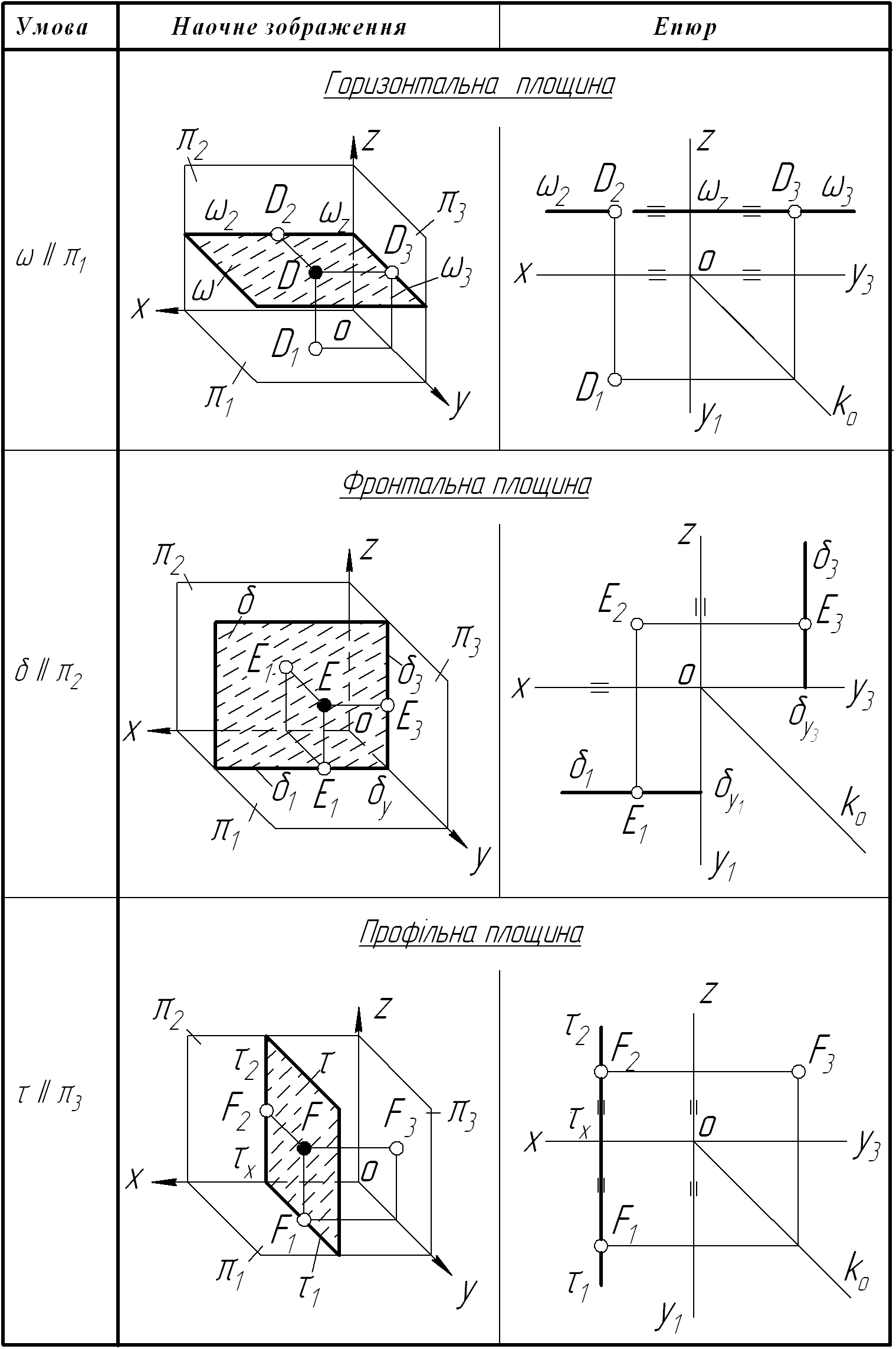
Площина, паралельна до 1, – горизонтальна.
Площина, паралельна до 2, – фронтальна.
Площина, паралельна до 3, – профільна.
Назва площини рівня вказує на те, до якої площини проекцій дана площина паралельна. Ці площини мають у системі трьох площин проекцій тільки два сліди, бо до третьої вони паралельні. На площину проекцій, до якої задана площина паралельна, будь-яка множина точок, лінія, плоска фігура, що знаходиться у двічі проекційних площинах, проеціюватимуться в дійсну величину, а на двох інших площинах проекцій проекції цих елементів співпадуть зі слідами площини (за збираючою властивістю проекційної площини).