Продовженя рисунка 5.10

Спосіб суміщення. Суть способу суміщення полягає в тому, що задану площину, обертанням навколо одного із її слідів суміщають з відповідною площиною проекцій. При цьому геометричні елементи, які розміщені в заданій площині, проеціюються на дану площину проекцій у дійсну величину і зберігають взаємне розміщення.

Спосіб суміщення можна розглядати як частковий випадок способу обертання площини навколо нульової горизонталі або фронталі.

Якщо площину обертати навколо її горизонтальногот сліду, то площина суміститься з площиною ₁, а якщо навколо фронтального сліду, то площина суміститься з площиною проекцій ₂.

Спосіб суміщення використовують:

• при визначенні дійсної величини і форми геометричних елементів, які лежать у даній площин;

• при побудові проекцій геометричних елементів, розміщених у заданій площині за їх заданою величиною і формою (обернена задача).

На рисунку 5.11 показано побудови, які виконуються при суміщенні площини загального положення  з площиною проекцій ₁. Віссю обертання в даному випадку служить горизонтальний слід ₁ площини . Якщо сумістити з площиною ₁ фронтальний слід ₂ площини , тоді можна буде знайти суміщені положення будь-яких елементів заданої площини.

Д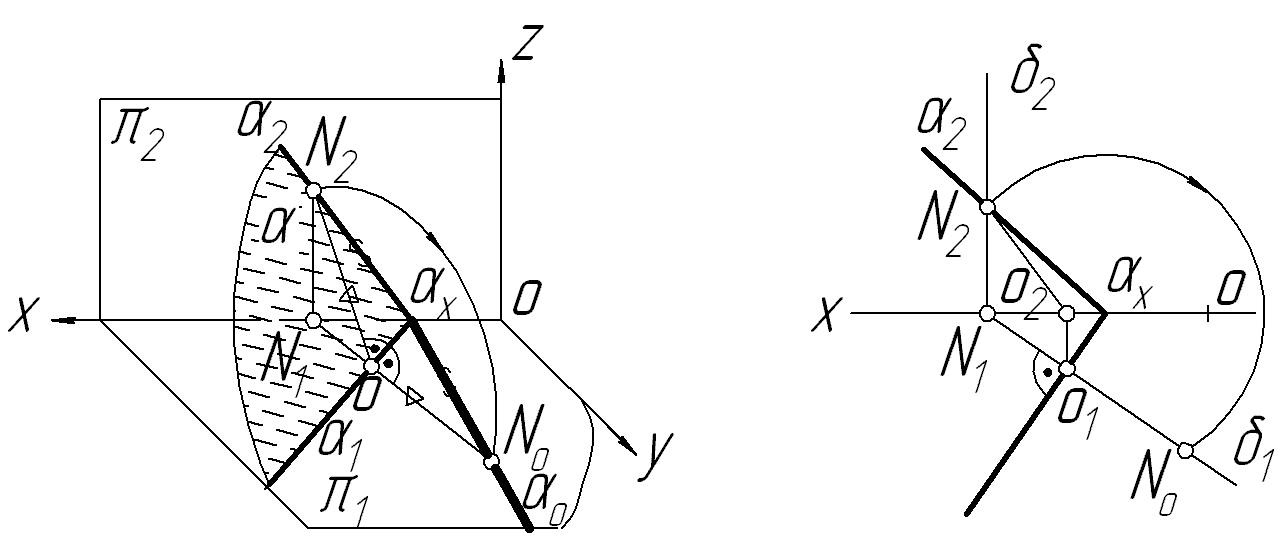 ля того, щоб знайти суміщені положення фронтального сліду площини ₀, необхідно взяти будь-яку точку N на ₂ і сумістити цю точку з ₁. Точка N, обертаючись навколо сліду ₁, опише дугу радіусом ОN. Центром кола є точка О. Горизонтальна проекція N₁ точки N буде переміщатися в площині обертання , по прямій N₁O₁, яка перпендикулярна ₁ і збігається з точкою N₀, при суміщенні останньої з площиною ₁ (рис.5.11а). З креслення видно, що N₂_xO=N₀_xO, оскільки обидва трикутники прямокутні, мають спільний катет О_x і рівні катети N₂O=ОN₀=радіусу кола. Отже, гіпотенузи цих трикутників також рівні _xN₂=_xN₀. Аналогічна побудова і суміщення заданої площини з площиною проекції ₂ з тією різницею, що тепер віссю обертання буде слугувати фронтальний слід площини, а суміщений горизонтальний слід будується за вибраною точкою на ньому.

а)

б)

Рисунок 5.11

З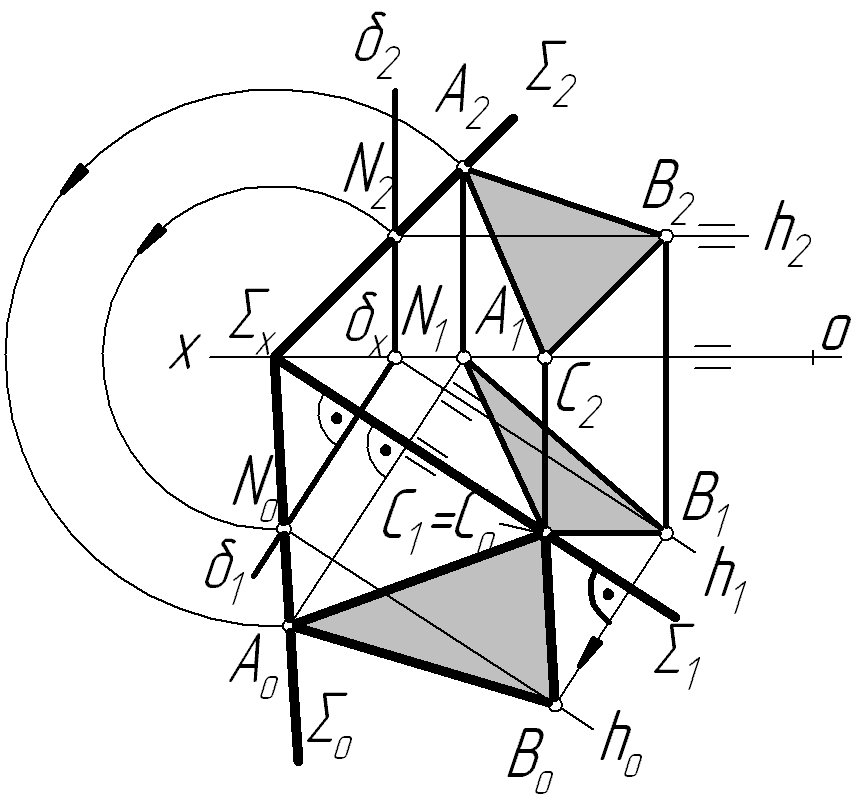 адача 4. Задано проекції трикутника АВС, який лежить у площині загального положення (рис.5.12). Знайти дійсну величину трикутника.

Д

Рисунок 5.12

ві вершини трикутника розміщені на слідах площини  (вершина А на сліді ₂, вершина С на сліді ₁). При суміщенні площини  з площиною проекцій ₁ вершина А збфгається із суміщеним слідом ₀ (точка А₀), вершина C залишиться на місці (оскільки вона лежить на горизонтальному сліді, який є віссю обертання); вершина В буде лежати на суміщеній горизонталі, яка проходить через точку В. Всі три вершини суміщені з площиною проекцій ₁, точки А₀В₀С₀ з’єднаємо між собою, як вершини суміщеного трикутника, що спроеціюється в дійсну величину.

Задача 5. Побудувати проекції кола, яке лежить у площині загального положення (рис.5.13).

Спочатку будуємо суміщену площину , в ній коло відповідного радіусу, а потім проекції кола. Проекціями кола, яке розміщене в площині  – загального положення будуть еліпси. Еліпси – проекції кола можна побудувати, якщо матимемо їх осі. Велика вісь 7-3 еліпса є горизонтальною проекцією кола і буде паралельна горизонтальному сліду площини, а по величині дорівнює діаметру кола 7₁-3₁; мала вісь 1-5 цього еліпса направлена по лінії найбільшого нахилу площини .

Велика вісь MN еліпса (фронтальної проекції кола) паралельна фронтальному сліду площини і дорівнює діаметру кола, а мала його вісь KL напрямлена перпендикулярно тому ж сліду площини.

Проекції кінців діаметрів кола, які переходять в осі еліпса, можна знайти так само, як визначаються проекції будь-якої точки площини за її суміщеним положенням. Так само можна побудувати будь-які проміжні точки заданих вище еліпсів.

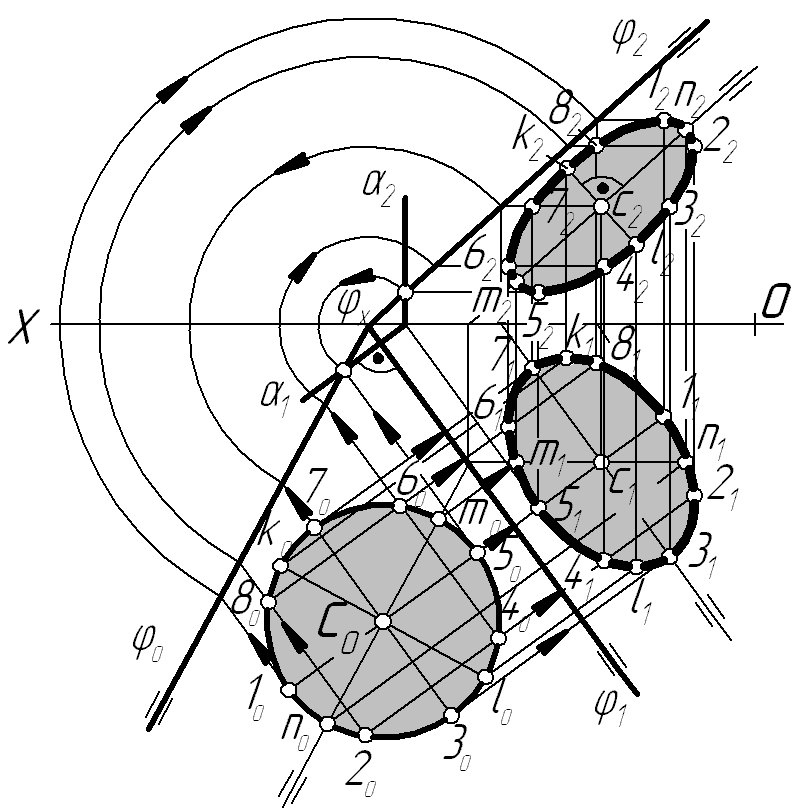
Рисунок 5.13

Задача 6. Побудувати проекції піраміди висотою Н, яка лежить своєю основою у площині , за суміщеними слідом ₀ і основою А₀В₀С₀ (рис 5.14).

П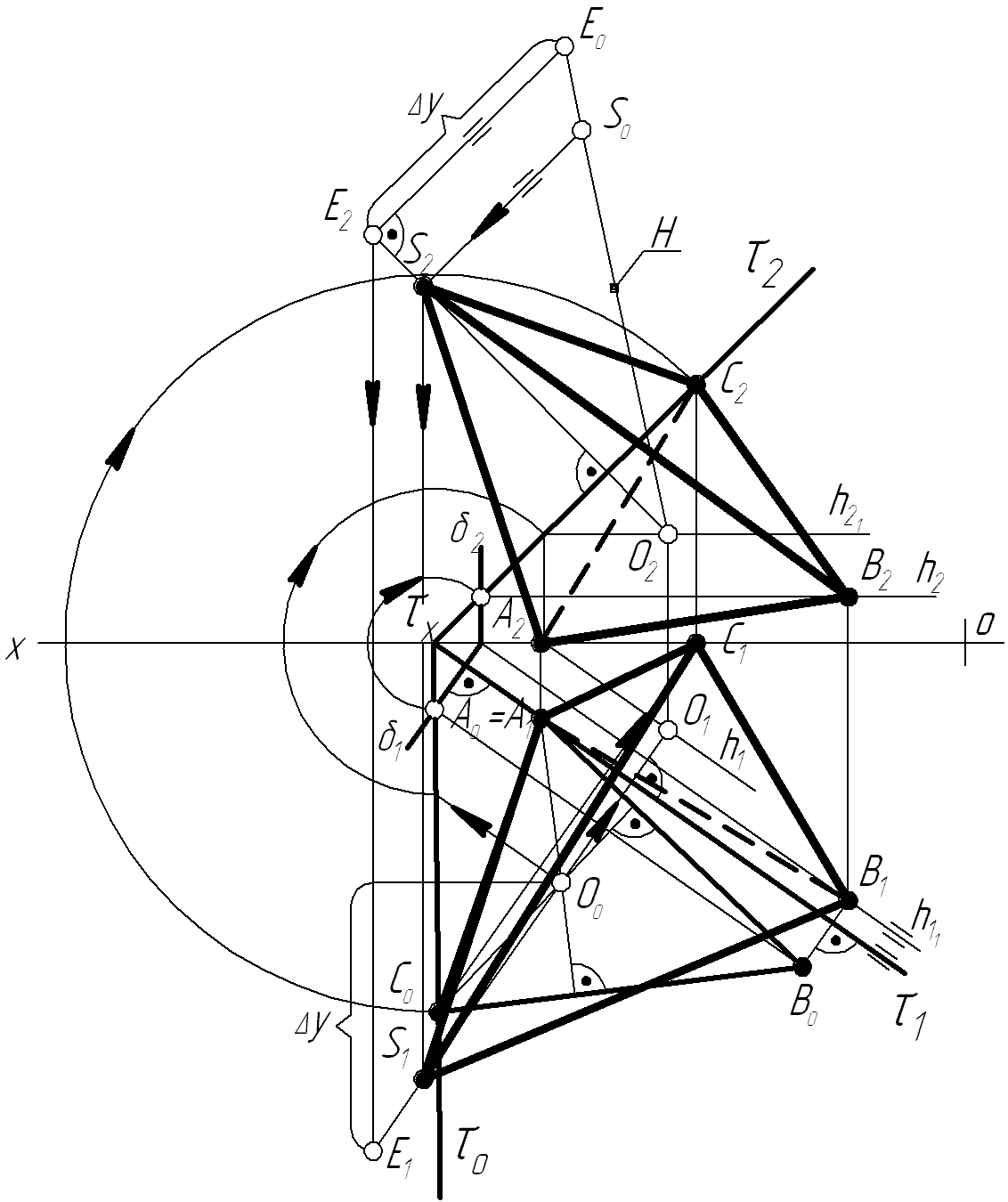 обудову почнемо з того, що знайдемо фронтальний слід площини ₂. Виберемо довільну точку на ₀ і піднімемо її у фронтальну площину за допомогою горизонтально-проекційної площини  (побудову показано стрілкою). Потім знаходимо точку О – основу висоти піраміди, яка лежить на перетині висот трикутника А₀В₀С₀ і також піднімемо в площину . З точки О(О₂ і О₁) будуємо проекції висоти піраміди, виставивши перпендикуляр до слідів площини ₁ і ₂. Обжежимо цей перпендикуляр у будь-якій точці Е і методом прямокутного трикутника знайдемо справжню величину ОЕ. На дійсній відкладаємо величину Н (висота піраміди) і знаходимо проекції S₂ і S₁. Вершину S(S₂,S₁) з’єднуємо з вершинами основи А(А₂А₁), В(В₂В₁) і С(С₂С₁) та одержимо проекції шуканої піраміди.

Рисунок 5.14