Дисципліна: „Надійність і діагностування світлосигнального обладнання аеродромів” Лабораторна робота №2

„Обробка експериментальних статистичних даних про відмови елементів технічних систем. Визначення закону розподілу випадкової величини.”

Мета лабораторної роботи – набути навиків щодо обробки експериментальних статистичних даних появи випадкової величини та визначення закону її розподілу.

Основні теоретичні відомості

Властивості випадкових величин описуються за допомогою законів розподілу, під якими розуміють будь-яке співвідношення, що встановлює взаємозв’язок між м­ожливими значеннями випадкової величини й відповідними їм імовірностями. Ці залежності можна представити у вигляді таблиць, графіків або аналітичних функцій.

Наприклад, при вивченні роботи підприємства, що випускає резистори, виміряли величину 100 резисторів з номіналом 500 Ом. В результаті одержали 100 різних значень, що лежать у діапазоні від 456 до 535 Ом. Як проаналізувати за цими значеннями якість продукції?

Часто використовується наступний метод. Розбивають весь діапазон спостережуваних значень випадкової величини (у цьому випадку величина опору резисторів) на деяку кількість рівних інтервалів. Кількість інтервалів беруть від 5 до 25 шт., що визначається числом наявних значень випадкової величини. Чим більший об’єм випробувань, або, як кажуть, об’єм вибірки, тим більша кількість інтервалів.

Розділимо весь діапазон отриманих значень опорів резисторів на 9 рівних інтервалів і занесемо результати у таблицю 1.

Таблиця 1 Статистичний ряд значень випадкової величини

Діапазон опорів резисторів, Ом	450 -460	460 -470	470 -480	480 -490	490 -500	500 -510	510 -520	520 -530	530 -540
Кількість резисторів, шт.	3	11	14	19	24	15	9	3	2

Одержимо табличну форму запису закону розподілу. Для наочності зобразимо отриману залежність у вигляді графіка, на якому по осі ординат відкладемо у відсотках кількість резисторів для відповідної ділянки (рис. 1а). По характеру отриманого графіка можна судити про якість резисторів, що випускаються заводом, про точність витримування технології. Чим вужче буде побудований графік і вище середній пік, тим більша якість продукції, що випускається заводом.

Експериментально отримані графіки розподілу випадкових величин називають гістограмами та будують їх у вигляді східчастої функції. Гістограма процентного розподілу випадкової величини має один значний недолік – при зміні кількості інтервалів розбивки істотно змінюються значення функції розподілу. Тому звичайно будуються графіки статистичної щільності розподілу випадкових величин:

, (1)

де N – загальна кількість елементів, що випробуються;

– кількість елементів, які своїми значеннями відповідають ділянці х.

У нашому прикладі статистичною щільністю розподілу буде залежність

При розбивці діапазону розподілу R на більше дрібні ділянки одержимо гістограму, що приблизно збігається з вихідною. Один з її можливих варіантів зображений пунктиром на рис. 1а. Гістограма щільності розподілу має цінну властивість – площа, обмежена нею, постійна і завжди дорівнює 1, адже, просумувавши всі окремі площі, одержимо величину, рівну

Необмежено збільшуючи число випробувань та інтервалів розбивки або спрямляючи ламану лінію, можна одержати гістограму у вигляді плавної кривої (рис. 1б).

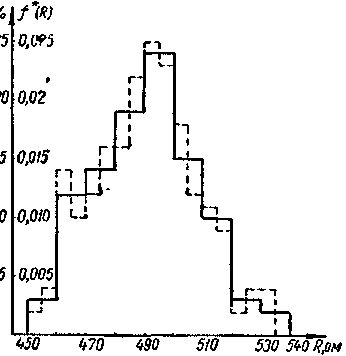
а б

Рис.1. а – гістограма щільності розподілу випадкової величини;

б – графік щільності розподілу випадкової величини.

Аналогічно тому, як частота появи події наближається до ймовірності виникнення події при нескінченно великій кількості випробувань, так і статистична щільність розподілу випадкової величини наближається до дійсної щільності розподілу. Якщо в результаті математичної обробки ряду випробувань одержано графік щільності розподілу випадкової величини f(x), то можна стверджувати, що повністю описані її властивості.

Функція розподілу випадкової величини має вигляд

(2)

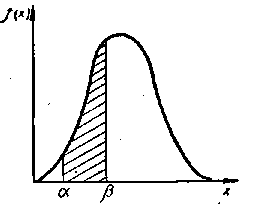
Кожна точка функції розподілу (2) показує ймовірність того, що випадкова величина набуде таке значення, що є меншим або дорівнює абсцисі х (див. рис.2). Ймовірність того, що випадкова величина прийме значення від  до  легко знаходиться як різниця ймовірностей

.

Рис. 2. Приклад графіку функції розподілу випадкової величини х, розподіленої за нормальним законом.

Функція розподілу, її похідна – щільність розподілу та параметри закону розподілу (математичне чекання та дисперсія) всебічно описують характеристики випадкової величини. Тому важливо, якщо закон розподілу випадкової величини заздалегідь невідомий, за результатами випробувань насамперед визначити закон розподілу, а потім визначати параметри цього закону.

Питання визначення закону вирішується остаточно лише при великій кількості випробувань за допомогою гістограм. При наявності ж невеликого числа відмов (один-два десятка), з яким найчастіше доводиться зустрічатися на практиці, визначити закон розподілу за допомогою гістограм неможливо. У цьому випадку застосовуються допоміжні штучні методи, що дозволяють оцінити можливість опису спостережуваного випадкового явища тим або іншим законом. Причому, як правило, маючи результати нечисленних випробувань неможливо сказати, що розподіл підпорядковується певному закону. Критерії оцінки звичайно побудовані на порівнянні відповідності результатів випробувань одному або іншому закону (або групі законів) і визначенні, якому з порівнюваних законів краще відповідають дослідні дані.

Виконуючи послідовно такі порівняння (кілька разів з різними законами розподілу), можна встановити, якому з розглянутих розподілів найкраще відповідають отримані дослідні дані. Оскільки доведено, що більшість технічних систем мають наробіток до відмови, розподілений за показовим законом, розглянемо два критерії, які дозволяють підтвердити гіпотезу про показовість закону розподілу відмов.

1.Перший метод є найбільш простим та грубим методом оцінки відповідності експериментальних даних показовому закону. Він базується на одній з властивостей показового закону розподілу випадкової величини – рівності математичного чекання і середньоквадратичного відхилення випадкової величини – рівність (3).

Т_ср = (3)

Отже, маючи статистичний ряд значень випадкової величини, необхідно обчислити значення і , порівняти їх між собою і, якщо рівність (3) виконується, можна припустити, що закон розподілу часу відмов близький до показового.

2. Другий метод – метод показового паперу базується на графічній побудові функції

, (4)

де Q(t) – імовірність відмови до моменту часу t. Оскільки функція

для показового закону на графіку є прямою лінією, емпірично побудований графік функції (4) повинен бути близький до прямої з тангенсом кута нахилу до осі абсцис, рівним інтенсивності відмов. Зазначений графік зручніше будувати на показовому папері, що має логарифмічний масштаб по осі ординат. Тоді не потрібно виконувати логарифмування. При звичайному рівномірному масштабі по осі ординат необхідно відкладати значення , тобто потрібно виконати логарифмування функції . Якщо випробування проводилися без відновлення елементів, що відмовили, то значення функції Q (t) знаходиться за формулою

, (5)

де N – кількість елементів, що проходили випробування;

п (t) – кількість елементів, що відмовили до моменту часу t.

Побудувавши отриману залежність слід графічно перевірити можливість її апроксимації прямою лінією (рис. 3). Як видно із графіка, для даної випадкової величини можна зробити висновок про те, що закон її розподілу є показовим.

Якщо в результаті побудови графіка функції (4) після апроксимації виходить нелінійна залежність, то гіпотеза про показовий характер розподілу не підтверджується. При цьому можна припустити, що розподіл підпорядковується закону Вейбулла з параметром >1, якщо крива має ввігнутий характер, і з параметром <1, якщо – опуклий. Зазначені криві нанесені у вигляді пунктирних ліній на графіку рис. 3 (а – опукла, б – увігнута).

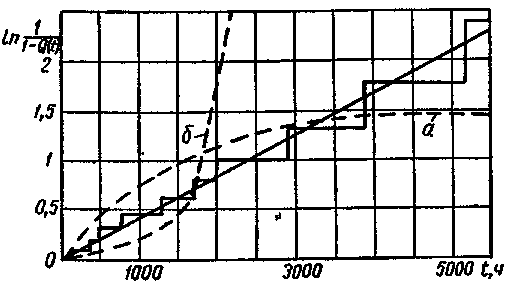
Рис. 3. Графік функції .

При використанні даного методу інтенсивність відмов елементів за допомогою графіку знаходиться за формулою (2):

, (6)

де K_Q, K_t – масштабні коефіцієнти;

 – кут нахилу функції (4) до вісі абсцис.

Масштабні коефіцієнти знаходяться за наступними формулами

, а , (7)

де S_Q і L – відповідно висота та ширина графіку функції (4);

f(t)_max – максимальне значення функції (4) (для нашого випадку f(t)_max = 2,4);

t – область зміни наробітку до відмови, знаходиться як t = t_max - t_min.

Беручи до уваги той факт, що інтенсивність відмов елементів  зворотно пропорційна наробітку до відмови Т₀, її значення за статистичними даними визначається за формулою

, (8)

де n(t) – кількість відмов, які відбулися за проміжок години t;

– сума годин наробітку усіх однотипних елементів, що випробувалися.