Расчет надежности с использованием формулы полной вероятности

В теории вероятности решается такая задача. События В зависит от того, какое частное состояние принимает событие А.

Событие А может принимать состояние А₁, А₂, А₃, …А_n, которые являются несовместимыми (т.е. не могут возникнуть одновременно два состояния: А₁ и А₂ и т.д.).

Если известны условия вероятности Р(В/А_i) и вероятности Р( Аi ), то полная вероятность события В равна

Пример: определить Кг комплекса с учетом надежности блока сопряжения, если комплекс состоит их двух машин и

1) блок сопряжения их исправен (машины работают в режиме резервирования);

2 блок сопряжения их неисправен (машины работают в автономном режиме). Коэффициент блока сопряжения Кг (БС)=0,95, одной машины Кг (М)=0,9; комплекса Кг (Р), работающего в режиме резервирования, равен 0,99.

Коэффициент готовности Кг комплекса с учетом надежности блока сопряжения

Кг=Кг (БС)Кг (Р)+[1-Кг(БС)] Кг (м)=0,95х0,99+0,05х0,9=0,9855

Расчет надежности с использованием производящей функции

Если вероятность (p) появления некоторого события при испытаниях меняется от испытания к испытанию (принимает значение p₁, p₂, ….,p_n), то, чтобы определить вероятность появления события 0,1,2,…, m раз, используется производящая функция

(3.1)

p_i – вероятность появления события при i-м испытании;

q_i- вероятность отсутствия события при i-м испытании ;

z – коэффициент при значении искомой вероятности;

n – количество испытаний.

Если при выполнении операции умножения (по формуле 3.1) z окажется в степени i, то это означает, что zⁱ является коэффициентом при вероятности того, что в n испытаниях будет иметь место событие i риз.

Пример: определить вероятности того, что при двух испытаниях число отказов будет 0,1,2, если известно, что при первом испытании вероятность отказа ; при втором - .

Производящая функция

Вероятность того, что отказов будет 2 равна 0,02

Вероятность того, что отказов будет 1 равна 0,26

Вероятность отсутствия отказов равна 0,72

Расчет надежности объекта по графу его переходов в различные состояния работоспособности с использованием дифференциальных уравнений академика а.Н. Колмогорова

Пусть объект исследования может находиться в некоторых состояниях, число которых конечно (равно n). Номера состояний 0,1,2,…n. Из i-го состояния в j- е объект переходит с постоянной интенсивностью λ_ij, обратно – с постоянной интенсивностью μ_ji.

Применение дифференциальных уравнений, для определения вероятностей состояний объекта, рассмотрим на примере объекта, изображенного на рисунке 3.4

1

2

а)

б) Граф состояний

Рис. 3.4

Число состояний три. Состояние S₀ – два элемента (1 и 2) – работоспособны. S₁ – один из элементов (1 или 2) – в отказовом состоянии, S₂ – оба элемента в отказовом состоянии.

По виду графа состояния можно составить систему дифференциальных уравнений Колмогорова по следующему правилу.

Для каждого из возможных состояний объекта записывается уравнение, в левой части которого dP_i/dt, а справа – столько слагаемых, сколько стрелок графа соприкасается с данным состоянием. Если стрелка направлена в данное состояние, то перед слагаемым ставиться плюс, если стрелка направлена из данного состояния - минус. Каждое из слагаемых будет равно произведению интенсивности перехода из данного состояния (либо в данное состояние) на вероятность состояния из которого выходит стрелка

Можно упростить уравнение, если учесть, что рассматриваемый процесс – процесс марковский стационарный, т.е. можно принять, что dP_i(t)/dt = 0

Четвертое уравнение при трех неизвестных необходимо, т.к. первые три уравнения сводятся к двум. Решение системы уравнений даст:

.

Результаты решения системы можно получить непосредственно по виду графа состояний, если пользоваться следующим правилом: вероятность нулевого состояния определяется выражением:

,

где числитель правой части – всегда единица; знаменатель - сумма, состоящая из единицы и дробей, числители которых – произведения интенсивностей на верхних стрелках, знаменатели – произведения интенсивностей на нижних стрелках (произведения формируются с последовательным увеличением числа множителей от одного до n в соответствии с переходами ).

Вероятность состояния равна вероятности состояния , умноженной на коэффициент равный второму слагаемому в знаменателе для , т.е.

Вероятность состояния равна вероятности состояния умноженной на коэффициент, равный третьему слагаемому в знаменателе для , т.е.

Вероятность n-го состояния равна вероятности состоянии , умноженной на коэффициент равный последнему (n-му), слагаемому в знаменателе для , т.е.

Пример: Определить вероятность состояний объекта, схема которого и граф состояний изображены на рис 3.4, если интенсивности отказов λ₀ элементов 1 и 2 равны 0,02, а интенсивности восстановления

Интенсивности переходов объекта в состояние S₀, S₁, S₂ равны:

Вероятность состояния S₀

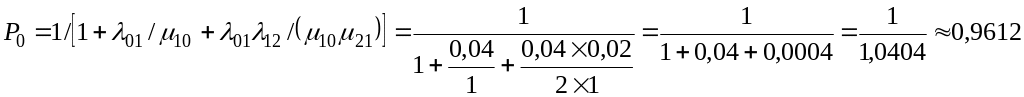
Вероятность состояния S₁