Применение умножения матриц

Схема Фалька может быть расширена на случай умножения нескольких матриц.

Заранее предполагая, что умножение приведенных матриц в требуемом порядке выполнимо.

П ример. Даны матрицы

, , .

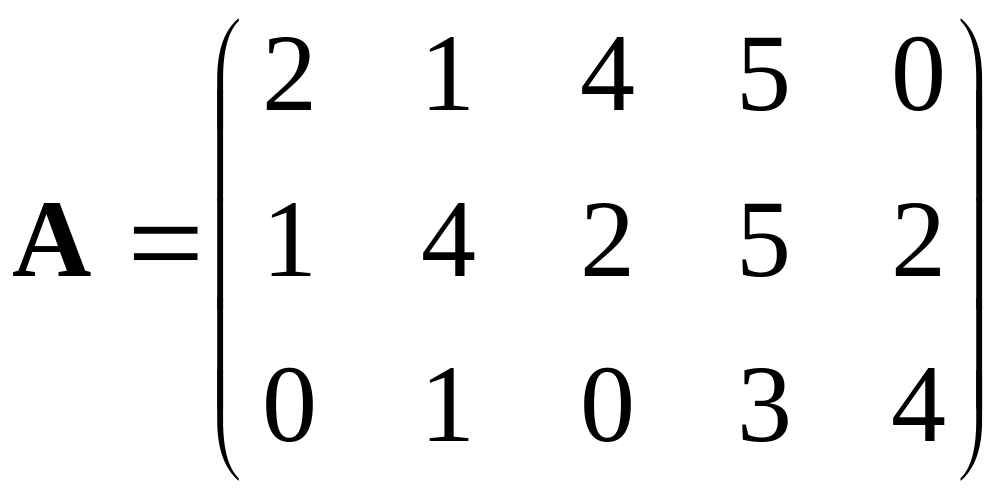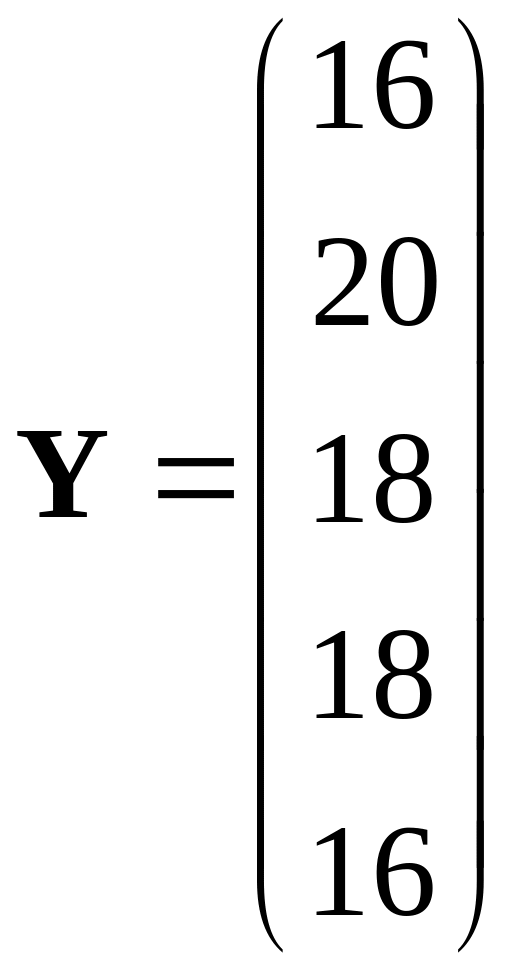Найти произведение .

▲ Расчет произведения целесообразно производить по схеме Фалька с горизонтальным расположением матриц (схема 1.3):

Схема 1.3.

Вычисление произведения, включая контроль посредством проверки столбцевых сумм, представлено на схеме 1.4:

									16
									20
				2	1	4	5	0	18	Y
			А	1	4	2	5	2 4	18
				0	1	0	3		16
	0	4	2	4	18	8	26	16	1292
B	0	2	4	2	12	4	22	20	1060	C
	5	1	0	11	9	22	30	2	1324
	5	7	6	17	39	34	78	38	3676

Схема 1.4 ▼

Свойства умножения матриц

После определения умножения матриц необходимо исследовать, верны ли для него известные законы умножения вещественных чисел: коммутативность, ассоциативность, дистрибутивность.

Коммутативность

Выясним, выполняется ли для умножения матриц закон коммутативности.

1. Исследуем, имеет ли смысл закон коммутативности для прямоугольных матриц.

Исследование проведём на числовом примере.

П ример. Найти произведения двух матриц

.

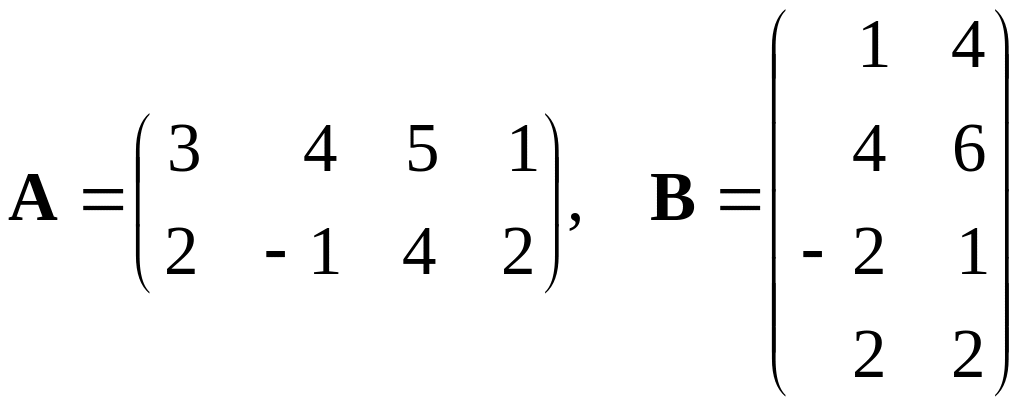▲ Число столбцов матрицы равно числу строк матрицы , поэтому определено произведение .

Число столбцов матрицы равно числу строк матрицы , поэтому определено произведение .

Применяя схему Фалька, получаем

				B	1	4	А В
					4	6
					–2	1
					2	2
A	3	4	5	1	11	43
	2	–1	4	2	–6	10

A			3	4	5	1
			2	–1	4	2	BA
B	1	4	11	0	21	9
	4	6	24	10	44	16
	–2	1	–4	–9	–6	0
	2	2	10	6	18	6

Оба произведения, и , здесь имеют смысл, но являются различными матрицами (даже различных порядков). ▼

2. Выясним, имеет ли место коммутативность при умножении квадратных матриц одного и того же порядка.

П ример. Найти произведение и двух квадратных матриц второго порядка

.

▲ Применяя схему Фалька, получаем

B					–2			3
					3			–5
A	2		5		11			–19		AB
	1		3		7			–12
		A				2	5
						1	3
B		–2		3		–1	–1		BA▼
		3		–5		1	0

Примеры показывают, что произведение двух матриц может не обладать коммутативным свойством, т.е. в общем случае

.

Эти же примеры показывают, что законы операций над вещественными числами не могут без доказательств переноситься на новые математические объекты.

Однако можно доказать, что существуют квадратные матрицы, удовлетворяющие равенству

.

П ример. Пусть

.

▲ Тогда

. ▼

М атрицы , для которых , называются перестановочными или коммутативными.

Очевидно, что это может иметь место только в случае, когда – квадратные матрицы одного и того же порядка.

Пусть – квадратная матрица порядка ,

– единичная матрица,

– нулевая матрица того же порядка.

Тогда

, .

Эти равенства легко получаются непосредственной проверкой.

Равенства означают, что при умножении матриц

• единичная матрица играет роль единицы,

• нулевая матрица – роль нуля.

Имеются, однако, и такие матрицы , что

,

хотя и .

Эти матрицы называются делителями нуля.

Замечание. Как известно, для вещественных чисел

тогда и только тогда, когда или .

В поле вещественных чисел делителей нуля не существует.

П ример. Даны матрицы

и .

Найти .

▲ .

Следовательно, – делители нуля. ▼