1.3. Умножение матриц

Введём сначала понятие согласованности матриц.

О пределение. Матрица называется согласованной с матрицей , если

• число столбцов матрицы равно

• числу строк матрицы

(если «ширина» матрицы равна «высоте» матрицы );

другими словами, матрица согласована с матрицей .

П ример. .

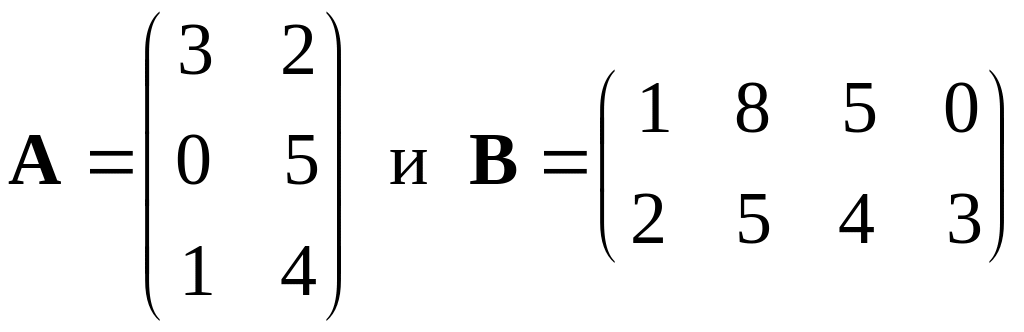Матрицы и являются «согласованными», поскольку матрица типа и матрица типа .

П ример. .

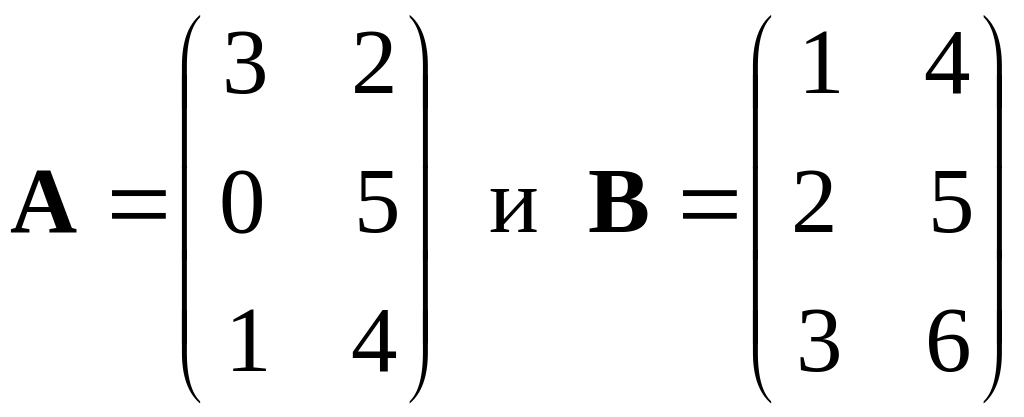Матрицы не являются «согласованными», т.к. матрица типа и матрица типа .

Отметим следующее:

1) если – квадратные матрицы одного порядка, то они взаимно согласованы (матрица согласована с матрицей , матрица согласована с матрицей );

2) из согласованности матрицы с матрицей не следует согласованность матрицы c матрицей .

П оясним это понятие на следующем примере.

Даны три матрицы

.

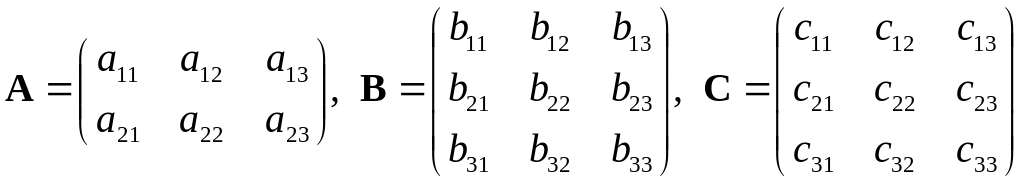Матрица согласована с матрицей :

м атрица имеет три столбца, матрица – три строки.

Матрица не согласована с матрицей (матрица имеет три столбца, матрица – две строки), но согласована с матрицей .

Матрица согласована с матрицей , но не согласована с матрицей .

О пределение. Если матрица согласована с матрицей , то их произведением называется матрица

,

элемент которой определяется по следующему правилу

Формула означает, что элемент матрицы равен

сумме произведений элементов строки матрицы

на соответствующие элементы столбца матрицы .

( строка матрицы умножается на соответствующие элементы столбца матрицы ).

Итак, согласно определению не всякие две матрицы можно перемножить.

Произведение двух матриц

имеет смысл тогда и только тогда, когда

Число столбцов первого множителя равно

числу строк второго множителя.

При этом в произведении получается матрица,

• число строк которой равно числу строк первого множителя,

• а число столбцов равно числу столбцов второго множителя.

Схематически последнее утверждение можно изобразить следующим образом:

∙

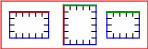
Что касается правила для вычисления элементов в произведении двух матриц, то его схематически можно изобразить так:

.

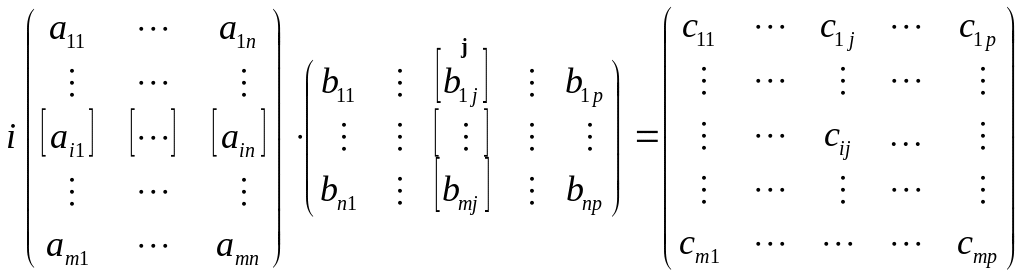
П ример. Перемножить матрицы

.

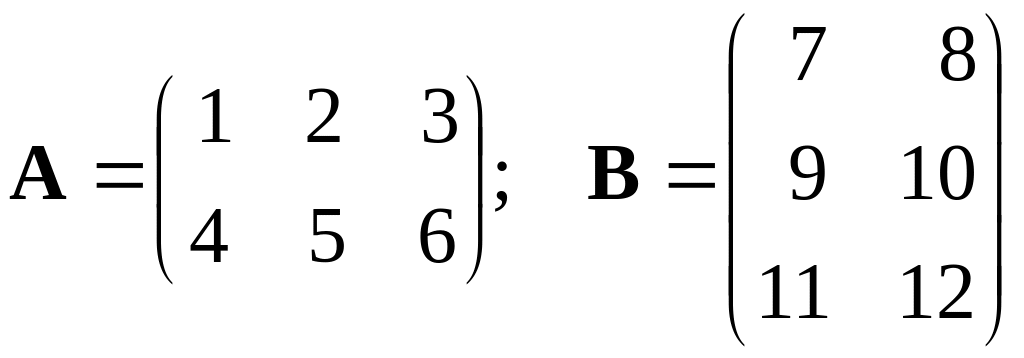▲ Произведение имеет смысл, поскольку число столбцов матрицы равно числу строк матрицы

. ▼

Пример. Перемножить матрицы

.

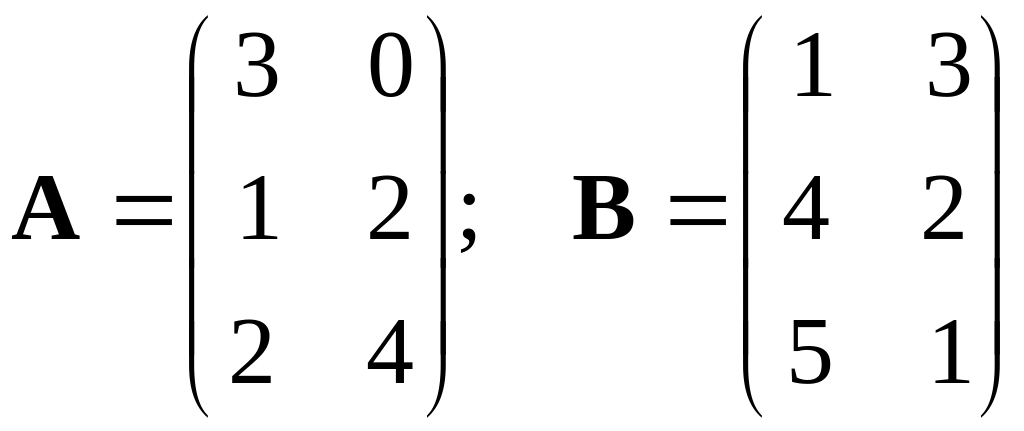▲ Матрицы одного типа .

Следовательно, они не согласованы и произведение не определено. ▼

Рассмотрим частный случай произведения матриц.

Пусть дана матрица-строка

и матрица-столбец .

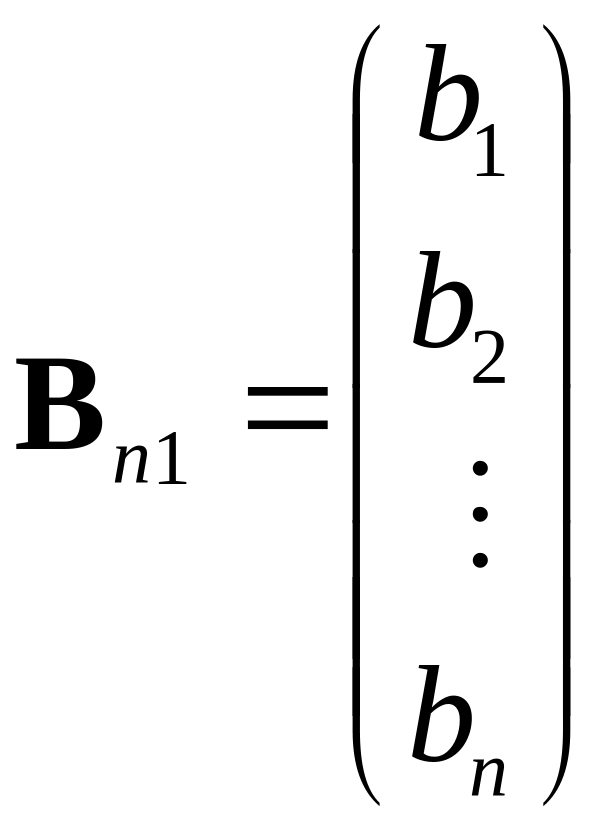Матрица имеет размер , причем её элемент

,

или

.

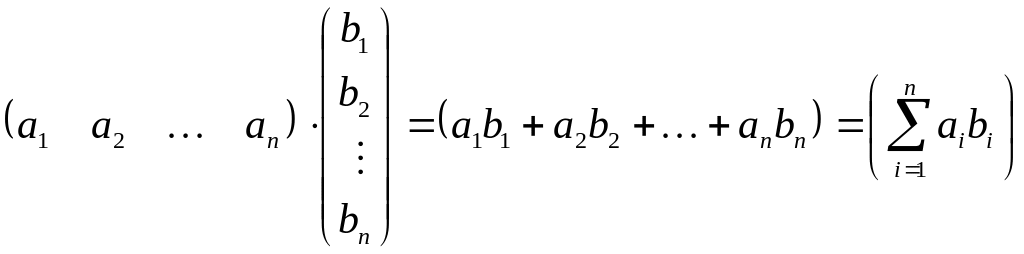П ример. Найти произведение матрицы-строки

на матрицу-столбец .

▲ .▼

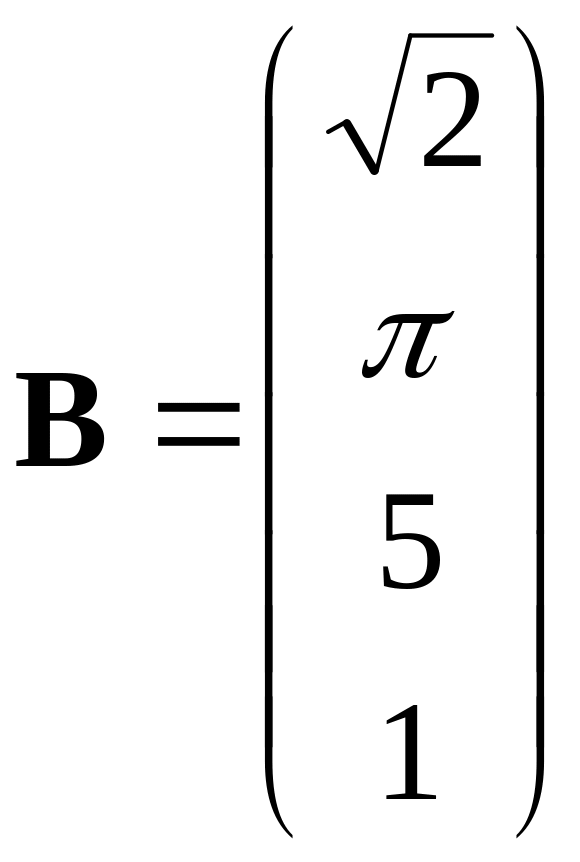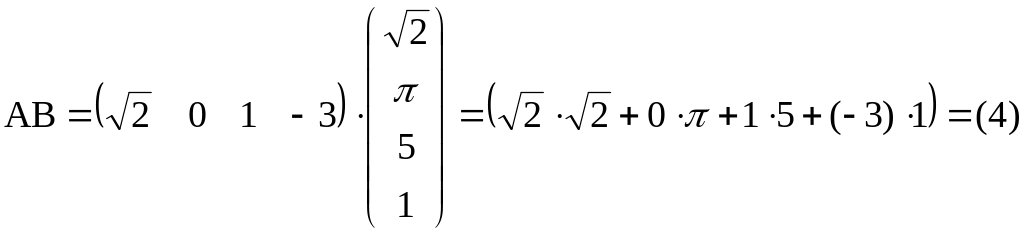Для того чтобы представить себе результирующую матрицу при перемножении двух матриц, может оказаться полезным представление матриц в виде прямоугольных блоков

A ∙ = C ∙ B = A ∙ B = C

B A C

Вычисление произведения матриц

Умножая матрицы вручную, целесообразно расположить их удобным способом.

Для этого может употребляться, например, схема Фалька, причем заранее предполагается, что для данных матриц операция умножения выполнима.

Схема Фалька для умножения двух матриц

Расположим умножаемые матрицы и произведение матриц таким образом, чтобы элемент матрицы-произведения лежал на пересечении строки и столбца (схема 1.1).

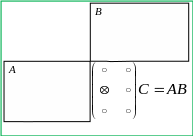
Схема 1.1.

П ример. С помощью схемы Фалька найти произведение матриц

▲ .

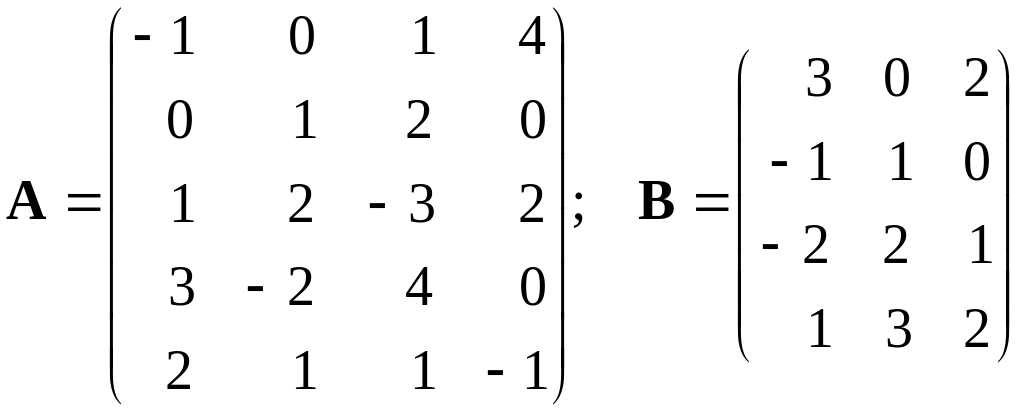	B	3 –1 –2 1	0 1 2 3	2 0 1 2
	–1 0 1 4	–1	14	7
	0 1 2 0	–5	5	2
A	1 2 –3 2	9	2	3
	3 –2 4 0	3	6	10
	2 1 1 –1	2	0	3

Схема 1.2 ▼