Веретенников
Валентин Николаевич
ВЫСШАЯ МАТЕМАТИКА
Э
ЛЕМЕНТЫ
ЛИНЕЙНОЙ АЛГЕБРЫ
Ρ Г Γ М У
Санкт-Петербург
2014
МАТРИЦЫ
Историческое развитие понятия «матрица»
В 1850 г. английский математик Дж. Дж. Сильвестр (1814-1897) ввёл в математику понятиме «матрица» для обозначения прямоугольного упорядочения чисел.
С 1853 г. к изучению матриц приступил В.Р. Гамильтон (1805-1865), а с1858 г. ‒ А. Кэли (1821-1895).
Основополагающее значения понятия матрицы для математики было осознано лишь в конце XIX в.
Существенную роль в дальнейшем развитии ма ричного исчисления сыграл Г. Фробениус (1849-1917).
Созданное алгебраистами исчисление было в 1925 г. использовано В. Гейзенбергом (1901-1976) для описания квантовой механики.
В 1942 г. Фельдткайлер ввёл матричное исчисление в электротехнику для расчета электрических цепей.
Ряд примеров, взятых из разных областей человеческой деятельности, покажет целесообразность введения нового математического понятия «матрица».
В
водный
прмер. Э.Ю. Берг, исследуя
наиболее выдающиеся ливневые дожди
разной продожительности на территории
Европейской части за десятилетие
(1903-1912), отметил занальную редукцию
передельной интенсивности дождей.
Крайние значения ливневых осадков
Зона |
Слой осадков (мм) за время
|
|||
15 мин |
30 мин |
1 ч |
2 ч |
|
Юго-западная |
40 |
60 |
80 |
110 |
Центральная(южнее Москвы) |
30 |
45 |
60 |
80 |
Северная |
20 |
30 |
40 |
55 |
Можно извлечь из таблицы ряды приведённых в ней чисел и записать их в следующей форме:
,
где содержательное значение каждого показателя определяется его местом в данном массиве.
Числа, записанные в строку, характеризуют слой осадков в одной зоне различной продолжительности.
Числа в столбце ‒ предельную интенсивность дождей конкретной продолжительности в различных зонах.
Таким образом, место, занимаемое числом в массиве, характеризует интенсивность продолжительности дождей в каждой зоне.
1.1. Основные определения
Рассмотрим множество
чисел
,
при каждом из которых стоят буквы
и
,
называемые индексами
(
первым,
вторым).
Будем считать, что
пробегает множество
натуральных чисел от 1 до
,
а
– от 1 до
.
При сделанных
предположениях число
при любых значениях
и
принадлежит множеству
.
У
словимся
располагать элементы
множества
в виде прямоугольной таблицы,
заключенной в круглые скобки и
состоящей из
строк и
столбцов, причем
таким образом, чтобы каждый элемент
(читается: «а-и-жи») занимал
строку и
столбец этой
таблицы.
Н
апример,
элемент
(читается: «а-три-пять») будет расположен
в этой таблице в третьей
строке и пятом
столбце.
О
пределение.
Матрицей
называется множество
чисел,
расположенных
в прямоугольной таблице из
строк и
столбцов.
Числа этой таблицы называются элементами матрицы.
Элементами могут быть числа из любой известной числовой области (натуральные, дробные, рациональные, целые, вещественные, комплексные), а также величины, функции или другие математические объекты (в том числе опять матрицы).
Условимся, что в дальнейшем изложении всегда, если не оговаривается противное утверждение, элементами матриц являются вещественные числа.
Матрица является краткой, ясной и наглядной формой описания и формулирования линейных взаимосвязей в математике, естествознании, технике и экономике.
Условимся сначала об одном весьма удобном способе обозначения элементов матрицы.
Место каждого элемента в матрице вполне определяется указанием номера строки и номера столбца, в которых находится наш элемент.
Чтобы в обозначении элемента отразить его местонахождение в
матрице, уславливаются все элементы матрицы обозначать одной буквой, но снабжать её двумя индексами, из которых
один обозначает номер строки,
а второй – номер столбца.
Обычно эти индексы пишут справа внизу, причем
сначала ставят номер строки,
а рядом – номер столбца.
Н
апример,
есть элемент
матрицы,
расположенный во второй
строке и в пятом
столбце.
Элемент
матрицы, стоящий
на пересечении
строки с номером
(номера
строк
считаются сверху
вниз) и столбца
с номером
(номера
столбцов
считаются слева
направо), обозначается через
;
числа
называются индексами
элемента.
Упорядоченная совокупность элементов
– первая строка
матрицы,
– вторая строка
и т.д.,
упорядоченная совокупность элементов
– первый столбец,
– второй столбец
и т.д.
В печатном тексте матрицы обозначаются прописными буквами латинского алфавита.
Для матрицы приняты также следующие обозначения:
.
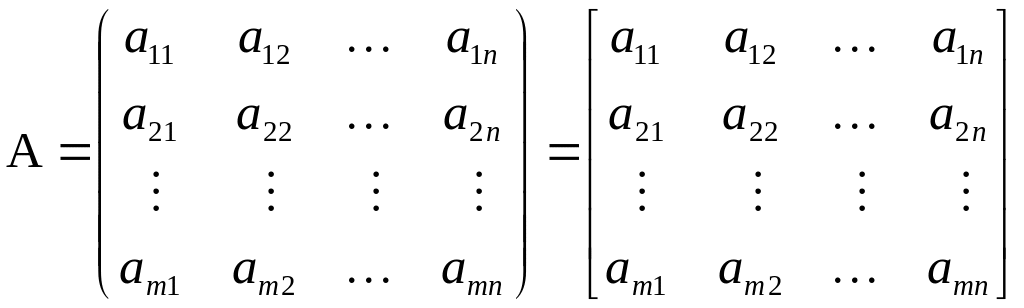Употребляются и более краткие обозначения
.
В дальнейшем будем пользоваться обозначением матрицы с круглыми скобками.
М
атрицу,
имеющую
строк и
столбцов, называют
матрицей типа
(читается «
»).
В отдельных случаях употребляется также термин «размер матрицы».
То, что матрица
имеет тип
,
обозначается следующим
образом:
.
Если
,
матрица называется
прямоугольной.
Две матрицы, имеющие одинаковое количество строк и столбцов, называются матрицами одинакового типа.