10.10. Определение вынужденных потерь скорости, связанных с заливанием, на основе зрительного впечатления в модельном эксперименте

Другим способом определения вынужденных потерь скорости из-за заливания может быть использование информации, которая содержится в модельных экспериментах [1,15,16]. Условие отсутствия интенсивного зарывания по всей длине пробега испытывавшейся модели имеет на встречном регулярном волнении в соответствии с указанными экспериментами с учётом [2,8] следующий вид:

(10.20)

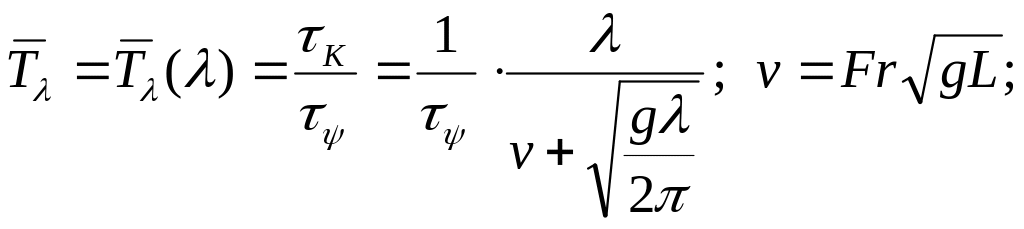
(10.21)

где - высота надводного борта на четвёртом теоретическом шпангоуте, - период килевой качки, - безразмерный (в долях длины судна) продольный радиус инерции масс, - высота и длина регулярной волны, - кажущийся период регулярной волны.

Коэффициент приближённо определяется как отношение максимальных ординат амплитудно-частотных характеристик относительных перемещений от продольной качки для проектируемого судна и для моделей, которые исследовались в работе [15] при постоянном числе Фруда. Эти максимальные ординаты находятся по приближённым формулам [2]. Тогда коэффициент вычисляется в функции главных элементов проектируемого судна, а коэффициент - в функции главных элементов рассмотренных в эксперименте [15] моделей. Эти модели имели следующие характеристики:

, , .

Тогда, с погрешностью не более нескольких процентов, и окончательно

(10.22)

Далее в работах [1,15,16] по зрительному впечатлению оценивалась степень зарывания, и в координатах при постоянном числе Фруда строились кривые вида , отделяющие зону отсутствия зарывания от зоны, где зарывание имеет место. Эти кривые мы приводим в табличной форме (таблица 10.4), [8,15]. В таблице 10.4 при и имеем , а во всех других случаях возможна линейная интерполяция.

Теперь необходимо найти нормативную вероятность зарывания как вероятность случайного события, состоящего в том, что Пусть на стационарном волновом режиме есть совместный дифференциальный закон распределения высот и длин волн. Тогда

В этих формулах есть граница области в координатах , вверх от которой опасное зарывание корабля имеет место, а вниз от которой - нет. Интегрирование распространяется лишь по одну сторону границы . Положение этой границы определяется условием . Зависимость отвечает некоторому заданному числу Фруда.

Определение зависимости мы уже рассмотрели (это формула (5)). А зависимость должна определяться по таблице 1 в функции параметра

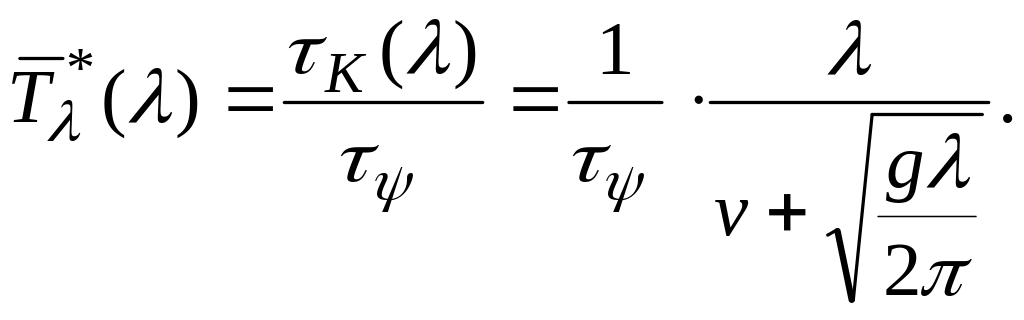
Здесь под величиной понимается уже длина элементарной гармонической нерегулярной волны.

Таблица 10.4

Определение зависимости граничного показателя зарывания от параметра .

Число Фруда	Значения при , равном:
	0,75	1,0	1,25	1,50	1,75	2,0	2,5	3,0
0	-	-	-	-	-	2,5	1,5	1,4
0,200	-	-	2,5	1,2	0,75	0,70	0,90	1,2
0,265	-	3,0	1,20	0,70	0,57	0,63	0,80	1,0
0,330	3,0	1,5	0,78	0,48	0,47	0,55	0,72	0,85
0,400	2,5	1,0	0,55	0,40	0,45	0,50	0,65	0,70

Тогда функциональная зависимость вида , которая представляет собой аналитическое выражение границы области , с учётом того, что в этом случае при заданном числе Фруда определится как

Рассмотрим теперь случай, когда распределения высот и длин волн являются не зависящими друг от друга. Тогда совместный закон распределения этих величин определяется как произведение соответствующих маргинальных распределений, так что . В этом случае имеем:

;

и, вычислив внутренний интеграл, приходим к соотношению

.

Здесь есть интегральный закон распределения высот волн. Пусть теперь и представляют собой распределения Рэлея. Тогда

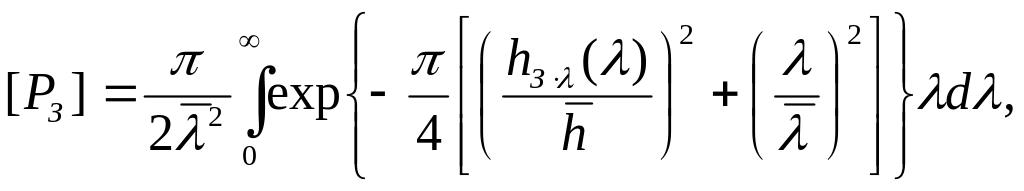
где - средняя высота и средняя длина нерегулярных волн.

Далее два параметра совместного распределения высот и длин нерегулярных волн - величины и - заменим одним параметром - высотой волны 3%-обеспеченности , применив для этого зависимости

измеряется в метрах;

где - средний период и средняя частота нерегулярного волнения.

Тогда окончательно находим

(10.23)

Рассмотрим далее предельные случаи, которым должно отвечать соотношение (10.23). Нетрудно показать, что при , что отвечает отсутствию надводного борта и максимальному зарыванию, имеем . Действительно, если обозначить , то окажется, что в этом случае

Для , что отвечает бесконечно большому надводному борту и гарантированному отсутствию зарывания, имеем . В реальности . На рис. 10.2 построены графики для нормативного коэффициента безопасности по зарыванию

.

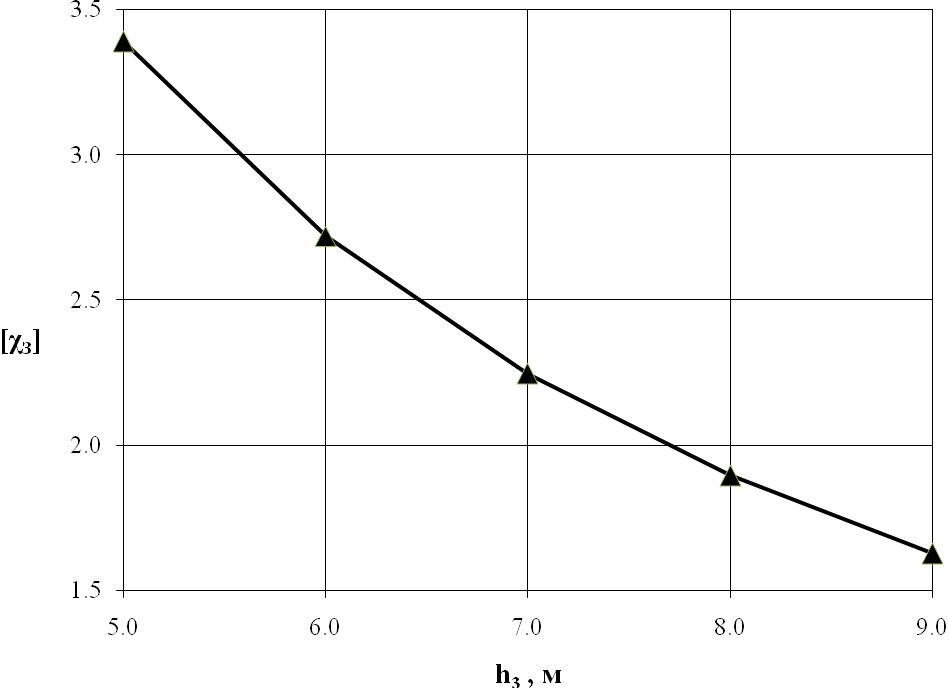
Рис. 10.2. Зависимость нормативного коэффициента безопасности от высоты волны 3%-обеспеченности

Зависимость коэффициента безопасности от параметра в реальном диапазоне изменения этой величины оказалась мало существенной (график рис. 10.2 отвечает ).

Очевидно также, что для всякого судна может быть установлена высота волны 3%-обеспеченности такая, при превышении которой начнётся вынужденное снижение скорости для избежания чрезмерного зарывания. Эта величина, которая представляет собой один из показателей мореходности проектируемого судна, [7], найдётся из условия

где высота надводного борта и дисперсия относительных перемещений могут быть отнесены к первому теоретическому шпангоуту.