10.5. Естественные потери скорости корабля, связанные с разгоном гребного винта при качке

Поправка к коэффициенту потери скорости на разгон гребного винта согласно работе [193] определится для встречного нерегулярного волнения в виде:

где , - частота вращения и диаметр винта;

- расчётная вероятность кавитации винта;

- расчетное погружение оси винта;

- то же при неработающем винте и отсутствии волнения (это геометрическое отстояние оси винта от КВЛ);

-статический подъем воды над гребным винтом, обусловленный влиянием корабельных волн; определен по эмпирической формуле Холтропа [456];

- понижение уровня воды над винтом, обусловленное работой гребного винта и функция понижения уровня;

- коэффициенты попутного потока и засасывания;

- коэффициент нагрузки винта по упору;

- функция Бесселя первого порядка мнимого аргумента;

- дисперсия относительных перемещений от продольной качки в районе расположения гребного винта.

_{При этом в соответствии с расчётными графиками справочника [387] можно принимать}

.

Величины и определены по теоретическим зависимостям А.М. Басина [387] (пространственная задача о работе идеального движителя под свободной поверхностью); величину можно также найти по таблице 4.18. Вероятность может рассматриваться либо как вероятность превышения коэффициентом диаметра-упора его критического значения, [193], либо как вероятность превышения расчётным погружением оси винта его критического значения, [206]. Под критическими значениями в обоих случаях понимаются такие значения указанных параметров, при которых появляется прорыв атмосферного воздуха к винту.

Второй подход оказывается более простым, и соответствующие зависимости приобретают вид, [206]:

где - число Фруда по частоте вращения гребного винта.

Таблица 10.3

Определение функции понижения уровня для гребного винта

Величины	Величины при , равном:
	0,5	1,0	1,5	2,0
1,0	0,29	0,53	0,59	0,58
1,1	0,20	0,44	0,52	0,53
1,2	0,13	0,37	0,47	0,48
1,3	0,08	0,31	0,41	0,43
1,4	0,07	0,26	0,38	0,41
1,5	0,06	0,24	0,36	0,38
1,6	0,05	0,20	0,32	0,35
1,7	0,04	0,15	0,26	0,31
1,8	0,03	0,12	0,23	0,28

Если ускорение измеряется в , то численно будем иметь . Поэтому число Фруда по частоте вращения винта иногда записывается в виде

,

где частота вращения винта измеряется в и диаметр винта измеряется в метрах.

10.6. Определение вынужденных потерь скорости корабля на основе осреднённых за время действия стационарного волнового режима нормативов слеминга и заливания. Анализ недостатков данного подхода и выбор путей их преодоления

Осталось найти способ расчётной оценки величины η_v2. Эта задача весьма актуальна для случая движения небольшого корабля на интенсивном волнении, когда высота волны 3%-обеспеченности h₃ заметно превышает величину [h₃], при превышении которой начинается вынужденное снижение скорости.

Предварительно перед нахождением коэффициента η_v2 необходимо, очевидно, найти нормативы по тем указанным выше характеристикам продольной качки, при превышении которых имеет место вынужденное снижение скорости.

Такие нормативы приведены: для надводных кораблей в обзоре [6]. Предложенные различными авторами нормативы по соответствующим амплитудам, скоростям и ускорениям от продольной качки достаточно близки между собой. Что же касается слеминга и заливания, то здесь нормативы разных авторов существенно противоречат друг другу. Поэтому необходимо выяснить причины этого.

На современном этапе отсутствуют как общие зависимости для расчёта поправки η_v2, так и необходимые для расчёта указанного коэффициента зависимости для расчёта вероятностей отказов по слемингу и заливаемости. Вообще, расчёт коэффициентов η_v1 и Δη_v связан с формальным применением известных из теории корабля схем и методов. Расчёт коэффициента η_v2 связан с действиями командира корабля, и здесь получение аналитических зависимостей оказывается намного более проблематичным.

Будем далее рассматривать различные виды слеминга и заливания. При этом для слеминга i=1 отвечает днищевому слемингу при ударе бульбом, i=2 отвечает днищевому слемингу при ударе корпусом, i=3 отвечает бортовому слемингу, и I_C=3. Для заливания i=1 отвечает зарыванию и i=2- забрызгиванию, и I_З=2. Под зарыванием понимается обусловленное продольной качкой периодическое заливание судна сплошными неразрушенными потоками воды. Под забрызгиванием понимается обусловленное продольной качкой периодическое заливание корабля разрушившимися (утратившими сплошность) потоками воды (брызговыми струями).

Пусть , - вектор показателей, связанных с вынужденным снижением скорости на волнении, а - вектор эксплуатационных нормативов по этим показателям. ( есть квантор общности, и запись « » читается «для всех i»). Здесь , где есть количество показателей продольной качки, которые учитываются при вынужденном снижении скорости судна.

Показатели отвечают переменной интенсивности реального нерегулярного волнения и переменной скорости. При осреднении по всему времени действия стационарного волнового режима эти показатели получаются или в виде случайных величин

, ,

или в виде неслучайных величин

, .

Здесь D_ni есть неслучайная дисперсия амплитуд, скоростей или ускорений вертикальной или килевой качки, [P_ni] есть нормативная обеспеченность, а _i есть неслучайная средняя частота того или иного вида слеминга (заливаемости). Для стационарного процесса величина _i найдётся по формуле вида:

(10.12)

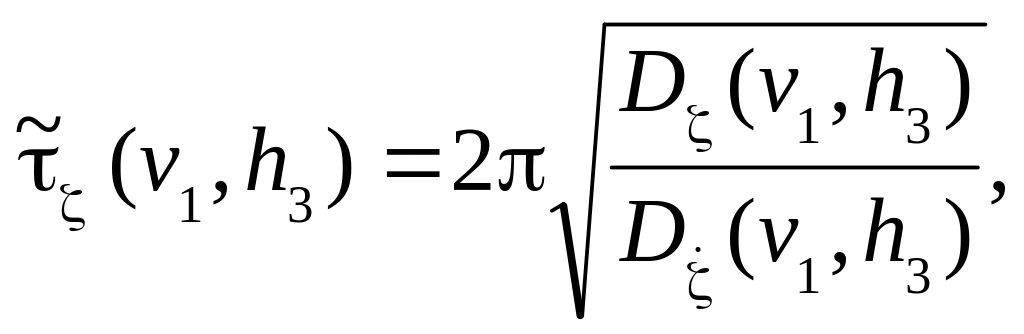
где _i- коэффициент безопасности для соответствующего вида слеминга или заливания;

- вероятность слеминга (заливания);

- средний период относительных перемещений от продольной качки;

- дисперсии относительных перемещений и скоростей относительных перемещений от продольной качки.

Коэффициенты безопасности для слеминга _i=_Ci, iI_C и для заливания _I=_Зi , iI_З определятся для расчётного поперечного сечения (обычно это первый или второй теоретический шпангоут) в виде:

где У_Сi, iI_C уровни относительных перемещений, при превышении которых возможен слеминг -ого вида, [2,8,9,18];

У_З1- уровень относительных перемещений, при превышении которого возможно зарывание [1,8,9,18]);

w_Ci , iI_C - расчётная скорость при слеминге -го вида, [2,8,9,18];

w_ПЗ- расчётная скорость, при превышении которой возможно забрызгивание, [8,9,18].

В первом приближении У_С1У_С2=Т, У_З1=Н_f - , где T - осадка, H_f- высота надводного борта и - статический подъём воды, основную часть которого составляет корабельная волна. Для уровня У_С3 и скорости w_ПЗ имеем более сложные зависимости вида:

- в градусах;

где b₀₂ ,b_ВП2 - ширина второго теоретического шпангоута по КВЛ и по верхней палубе;

b₀₅- ширина пятого теоретического шпангоута по КВЛ;

В- ширина судна;

- переходный коэффициент от скорости относительных перемещений к скорости брызгового потока в расчётном сечении;

_В- коэффициент, характеризующий встречное движение жидкости при погружении в жидкость шпангоутного контура в расчётном сечении в предположении, что жидкость является невесомой;

,- коэффициент полноты погруженной площади шпангоута и угол килеватости на уровне КВЛ в расчётном сечении;

Fr^*_S- пороговое число Фруда по скорости потока в расчётном сечении.

При определении пороговых скоростей при слеминге w_Ci , i=1,2 возможны такие два подхода:

-эти скорости определяются как такие минимальные, при которых вход в воду вышедшей перед этим из воды из-за продольной качки носовой оконечности судна ещё воспринимается как удар; в этом случае указанные скорости имеют смысл пороговых скоростей и w_Ci.=w_Пi, i=1,2;

-эти скорости определяются как такие минимальные, при которых ударные давления p становятся равными нормативным ударным давлениям [p], в этом случае указанные скорости имеют смысл опасных скоростей и w_Ci=w_pi, i=1,2.

При бортовом слеминге w_C3=0. При днищевом слеминге имеем

; ;

K_p1- коэффициент ударных давлений при слеминге бульба;

K_p2- коэффициент ударных давлений при ударе корпусом в условиях днищевого слеминга;

, g- плотность воды и ускорение свободного падения.

При нормировании слеминга (заливаемости) может также приниматься _i=_i, для слеминга _i=_Ci, iI_C, для заливания _i=_Зi, iI_З и соответственно [_i]=[_i], iI_C+I_З, а также _i=P_i и соответственно [_i]=[P_i], iI_C+I_З. Здесь .

Предположим, что зависимость _i =_i (v₁, h₃) монотонно возрастает по обоим аргументам. Тогда, если _i[_i], то η_v2=1 и вынужденного снижения скорости нет. Если же _i>[_i], , то такая ситуация недопустима, для её преодоления скорость вынужденно снижается, и η_v2<1.

Пусть сначала корабль движется на тихой воде со скоростью v₀ (в этом случае имеем i: _i=0), а затем на него начинает действовать волнение возрастающей интенсивности. С ростом высоты волны 3%-обеспеченности h₃ при медленно снижающейся по закону η_v1(h₃)v₀ скорости v₁(h₃) величина _i=_i [v₁(h₃),h₃] также растёт, и при некоторой интенсивности волнения h₃=[h₃] достигает нормативной величины . Тогда при 0h₃[h_3i] вынужденного снижения скорости нет, и в этом диапазоне интенсивностей волнения для -го показателя, имеем η_v2i=1. При h₃=h₃₀>[h_3i] имеем Равенству фактических _i и нормативных [_i] значений -го показателя отвечает скорость такая, что . Но тогда имеет место вынужденное снижение скорости, и имеем для -го показателя .

Выполнив ту же операцию для ряда значений h₃>[h₃], получим искомую зависимость вида η_v2(h₃, i), которая отвечает -му показателю. А для определения величины η_v2(h₃,) которая отвечает всем компонентам вектора , достаточно взять нижнюю огибающую зависимостей η_v2i(h₃, i), приняв

.

Рассмотрим теперь, почему предложения разных авторов в части нормирования тех частот слеминга и заливания, при превышении которых имеет место вынужденное снижение скорости, существенно различаются между собой. Дело здесь, по нашему мнению, в том, что основная нормативная характеристика слеминга и заливания - средняя частота _i- в существующих нормативах относится к одному удару (заливанию, формула (10.12)). Но на практике капитан судна отдаёт приказ о вынужденном снижении скорости в таких случаях:

-в случае слеминга - под впечатлением от нескольких сильных ударов подряд, [19];

-в случае зарывания - когда попавшая на палубу вода не успевает слиться за борт до нового зарывания, [10];

-в случае забрызгивания - под впечатлением от нескольких подряд мощных фонтанирующих всплесков над верхней палубой (палубой бака), [8].

Данные описания отказов нуждаются в численной конкретизации (что значит «несколько ударов (забрызгиваний) подряд» - два, три удара (забрызгивания) или больше, и каким промежутком времени они должны быть отделены друг от друга). Эти вопросы должны стать предметом будущих исследований, а далее мы будем предполагать, что соответствующие конкретные нормативы известны. Тогда под _i для всех iI_C+I_З следует понимать новые средние частоты _i=_i(v₁,h₃) определяемые по аналогии с формулой (10.12) как

(10.13)

где _i=_i(v₁,h₃) есть вероятности сформулированных только что отказов.

Соответствующий норматив [_i] =[_i], i I_C+I_З в первом приближении можно принять в виде , где - длительность стационарного волнового режима. Это означает, что вынужденное снижение скорости будет иметь место, если один из сформулированных только что отказов будет иметь место хотя бы один раз в течение времени .