10.4. Естественные потери скорости корабля, связанные с дополнительным сопротивлением из-за ветра и волнения

Оценка потерь скорости корабля из-за влияния ветра и волнения на должна в общем случае выполняться на основе уравнений статики и динамики пропульсивного комплекса. При этом уравнения статики определяют среднее за время действия стационарного волнового режима достижимую скорость корабля и соответствующую ей частоту вращения винтов, [193]. Вынужденные потери скорости должны учитываться дополнительно. Уравнения статики пропульсивного комплекса составляются на основе среднего дополнительного сопротивления на волнении и средних относительных перемещений кормовой оконечности. В уравнениях динамики пропульсивного комплекса рассматриваются колебания дополнительного сопротивления и периодические изменения частоты вращения винта, [193]. На начальных стадиях проектирования достаточно ограничиться одним уравнением статики пропульсивного комплекса. Тогда для стационарного ветроволнового режима приходим к следующей исходной зависимости, [343]:

(10.8)

где коэффициенты характеризуют естественные и вынужденные потери скорости, представляет собой поправку на разгон гребного винта из-за периодических выходов винта из воды при продольной качке.

Кроме того, в этих формулах есть скорость хода на волнении при отсутствии вынужденного её снижения в предположении, что рост сопротивления не влияет на кпд винтов, а предложенная в работе [389] поправка учитывает изменение кпд винта из-за роста сопротивления.

На интенсивном волнении искать коэффициент естественных потерь скорости приходится в алгебраической форме, и для достижимой скорости в условиях встречного ветра и волнения находим, [343]:

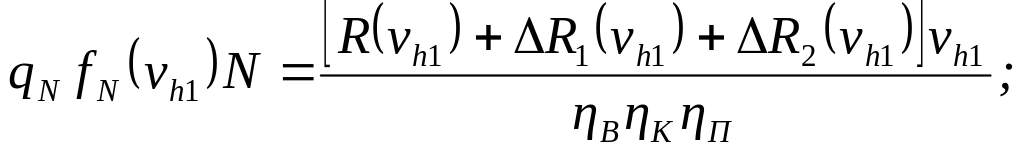(10.9)

где - мощность главных двигателей;

- коэффициент запаса мощности;

-функция, учитывающая зависимость ограничительной характеристики двигателя от скорости, определяется по рекомендациям работы [254], часть 3;

-полное сопротивление воды движению корабля при скорости ;

- сопротивление встречного ветра движению корабля при скорости , определяемое по соотношениям (10.1)-(10.2);

- сопротивление встречного волнения движению корабля при скорости , определяемое по соотношениям (10.3)-(10.5);

- кпд гребного винта;

- коэффициент влияния корпуса;

- кпд передачи (валопровода);

На слабом и среднем волнении искать коэффициент естественных потерь скорости можно в приращениях, используя дифференциальный метод. Тогда при постоянной мощности на встречном волнении будем иметь, [445,479]:

; (10.10)

В некоторых случаях задаётся приращение мощности на волнении , необходимое для сохранения заданной скорости. Если же фактически мощность остаётся постоянной, то, очевидно, снизится скорость. Этому естественному снижения будет отвечать коэффициент , равный, [22], [254] часть 3, [445,479]:

. (10.11)

Если влияние снижения кпд движителей на величину коэффициента незначительно (т.е. если приближённо справедливы соотношения ), то будем иметь .

Для поправки можно принять, []:

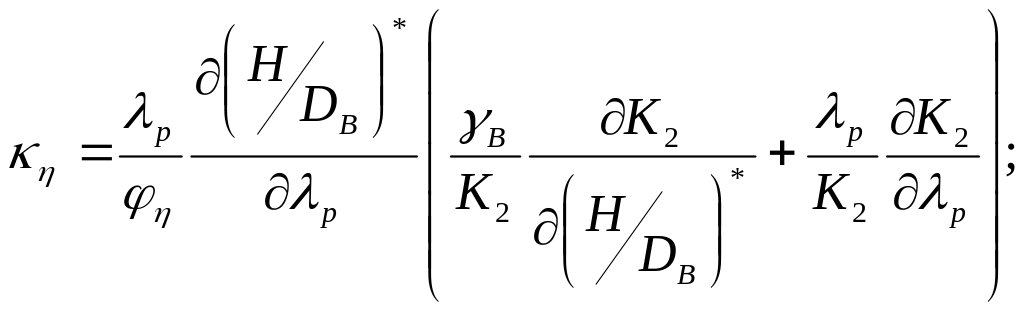
где - шаговое отношение гребного винта;

- относительная поступь гребного винта;

-коэффициенты упора и момента гребного винта;

-уравнение вида , решённое относительно ;

- показатель степени в формуле ,

Кроме того, при расчёте поправки на практике с достаточной точностью можно принимать также , [389].

На практике возможна и несколько иная постановка задачи расчёта ходкости на волнении. Возможно предъявление требования поддержания кораблём заданной скорости в условиях ветра и волнения заданной силы. Мощность главных двигателей , необходимая для достижения скорости на тихой воде, известна. Тогда в соответствии с поставленной задачей необходимо найти добавочную мощность такую, чтобы та же скорость была бы достижима и в условиях ветра и волн. Обычно приращение мощности существенно меньше исходной мощности . Тогда, применив по аналогии с соотношениями (10.10)-(10.11) дифференциальный метод, найдём:

где для встречного волнения и при осреднении по всему диапазону курсовых углов;

- пропульсивный коэффициент и его приращение при росте сопротивления на величину .

Определяя , введём такие допущения:

-приращение обусловлено изменением только кпд винта;

- приращение можно оценить по теории идеального движителя.

Тогда, приняв коэффициенты взаимодействия винта с корпусом малыми по сравнению с 1, найдём:

,

где - количество гребных винтов.

Все эти зависимости относятся к открытым некавитирующим гребным винтам и при переходе к движителям других типов они должны быть откорректированы.