34

10. Определение потерь скорости корабля в условиях ветра и волнения

10.1. Дополнительное сопротивление движению корабля из-за влияния ветра

_{В данной главе мы рассмотрим определение потерь скорости корабля на волнении. Для этого мы последовательно рассмотрим определение дополнительного сопротивления движению корабля, обусловленного ветром и волнением, а затем-определение естественных и вынужденных потерь скорости корабля.}

_{Дополнительное сопротивление корабля под действием ветра определяется формулой вида:}

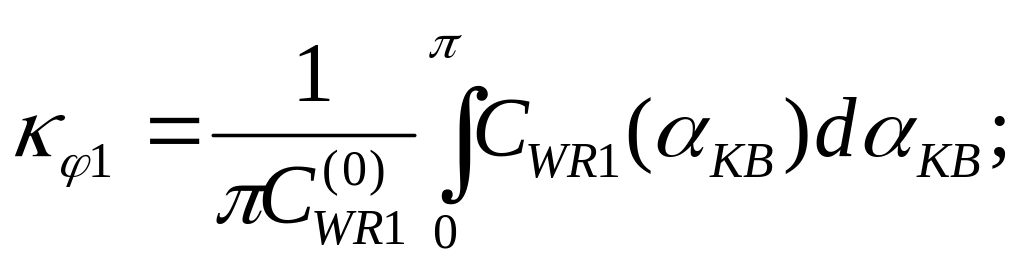
где - угол между направлением ветра и ДП корабля;

- расчётный угол, в функции которого определяется коэффициент аэродинамического сопротивления;

- расчётная скорость ветра как функция расчётной интенсивности волнения;

- площадь лобового сопротивления для проектируемого корабля;

- коэффициент лобового аэродинамического сопротивления;

- коэффициент аэродинамического сопротивления как функция угла .

Под углом в различных представлениях экспериментальных данных может пониматься как угол между направлением ветра и ДП корабля (т.е. угол ), так и угол между скоростью ветра и ДП корабля, . При встречном ветре, очевидно, будет , так что

Коэффициенты и определяются путём продувок в аэродинамических трубах, и при закритических числах Рейнольдса ( ) эти величины практически не зависят от скоростей воздушного потока. Величина для надводных кораблей имеет порядок 0,42-0,64, что меньше, чем у торговых судов (0,6-0,8).При этом до 60-80% от этой величины составляет сопротивление надстроек.

При волнении 3-4 балла и встречном ветре связанное с ветром дополнительное сопротивление составляет для надводного корабля 1,5%, а при ветре 7-8 баллов-до 3% от полного сопротивления воды движению корабля на полном ходу. Для угла величина коэффициента максимальна и составляет 1,3-1,4 от коэффициента . Далее с ростом угла коэффициент уменьшается и при этот коэффициент проходит через 0 и уходит в отрицательную область, достигая при примерно тех же (но с обратным знаком) значений, что и при , []. Поэтому величина интеграла получается весьма небольшой по абсолютной величине.

На практике величина определяется либо для встречного волнения, либо путём осреднения по всему диапазону курсовых углов, которые предполагаются равновероятными. В первом случае сопротивление и дополнительное сопротивление, обусловленное волнением примерно одного порядка. Во втором случае операция усреднения ведёт к тому, что сопротивление может иметь любой знак, но всегда .

10.2.Теоретические зависимости для дополнительного сопротивления воды движению корабля, связанного с волнением

Рассмотрим теперь некоторые аспекты определения дополнительного сопротивления движению корабля, обусловленного волнением. Вообще говоря, под действием волнения, которое представляет собой периодический процесс, корабль совершает колебательные движения по шести степеням свободы - в том числе вдоль продольной оси (продольно-горизонтальная качка) и вдоль поперечной оси (поперечно-горизонтальная качка). И тот и другой виды качки рассматриваются в теории качки как дополнительные (не основные). По физическому смыслу это означает, что восстанавливающие силы в обоих случаях отсутствуют, а получивший продольно-горизонтальное или поперечно-горизонтальное перемещение корабль остаётся в положении безразличного равновесия. Соответственно отсутствуют для этих случаев и частоты собственных колебаний, и корабль всегда совершает продольно-горизонтальную и поперечно-горизонтальную качку с частотой волнения.

Однако под действием волнения корабль совершает в продольно -горизонтальном и в поперечно-горизонтальном направлениях не только колебания (качку), но и совершает непериодические продольно-горизонтальные и поперечно-горизонтальные смещения. Чтобы преодолеть при поступательном движении корабля непериодическое продольно-горизонтальное смещение, приходится расходовать мощность главных двигателей на преодоление соответствующего продольного усилия. Это продольное усилие и будет представлять собой среднее дополнительное сопротивление на волнении. А непериодическое поперечно-горизонтальное смещение корабля под действием волнения носит название волнового дрейфа.

В основе представления реализации реального нерегулярного морского волнения лежит несобственный интеграл Фурье - Стилтьеса с нулевым нижним пределом в виде, [17]:

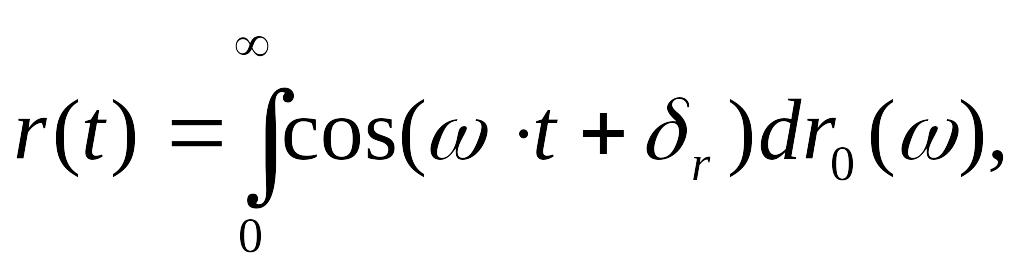
при этом выполнено условие

.

В этих формулах - дифференциал случайной амплитуды нерегулярного волнения как функция частоты элементарной гармоники нерегулярного волнения , - фаза, которая предполагается равномерно распределённой в интервале от 0 до , а символ означает операцию взятия математического ожидания от случайной величины . Кроме того, функция имеет нулевое математическое ожидание при всех , а также независимые приращения. Последнее условие означает, что

,

где - шаг по частотам.

Как показывают экспериментальные данные и соответствующий теоретический анализ, как среднее дополнительное сопротивление на волнении (термин «среднее» здесь означает, что рассматривается только непериодическая составляющая сопротивления), так и сила волнового дрейфа пропорциональны величине

.

Пусть теперь амплитуда некоторого процесса может быть представлена в виде , где есть оператор процесса . Тогда средняя амплитуда процесса А - величина - может быть представлена как

.

Это означает, что на регулярном волнении дополнительное сопротивление и сила волнового дрейфа пропорциональны квадратам амплитуд регулярных волн , при этом величины и зависят только от частоты , но не от амплитуды . Указанное обстоятельство находит полное подтверждение в эксперименте. Величины и носят название операторов дополнительного сопротивления и сил волнового дрейфа, а сами эти величины и на нерегулярном волнении определятся как

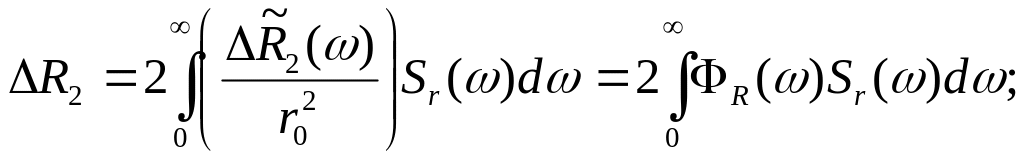
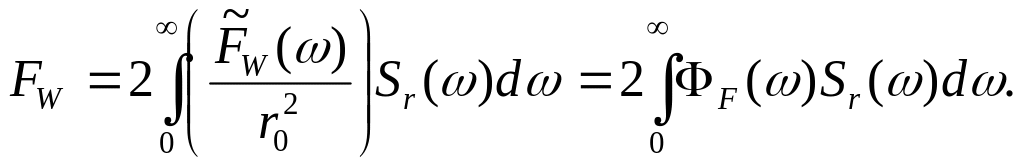
Отметим одно интересное обстоятельство. Как известно, на начальных этапах развития теории качки применялась т.н. гипотеза проницаемости, известная также как гипотеза А.Н. Крылова (в англоязычной технической литературе - гипотеза Фруда-Крылова). В соответствии с этой гипотезой присутствие в воде корабля не вносит никаких изменений в поле гидродинамических давлений. С использованием этой гипотезы можно с достаточной точностью рассчитать бортовую качку. Результаты расчётов продольной качки, а также волновых низкочастотных (т.е. изменяющихся с частотой волнения) изгибающих моментов получаются существенно завышенными, но в принципе эти расчёты могут быть выполнены. Результаты расчётов продольно-горизонтальной и поперечно-горизонтальной качки, а также внешние волновые нагрузки в некоторых специальных случаях (симметричный волновой изгибающий момент, действующий на мост катамарана) получаются заметно заниженными, но и эти расчёты в принципе можно выполнить. А вот выполнить корректные расчёты дополнительного сопротивления, равно как и сил волнового дрейфа (непериодического движения корабля под действием периодического волнового воздействия) на основе гипотезы проницаемости невозможно в принципе. Этот тезис был математически строго доказан Г.А. Фирсовым в 1950-х г.г. Расчёты волнового дрейфа привлекли внимание специалистов относительно поздно, где-то не ранее середины 1970-х г.г., когда доказательство Г.А. Фирсова было давно и хорошо известно. А вот по дополнительному сопротивлению на волнении было выполнено несколько принципиально ошибочных работ, в которых авторы принимали за основу гипотезу А.Н. Крылова. Не избежал этой ошибки даже такой авторитетный учёный-кораблестроитель, как Т. Хавелок.

Поэтому для чисто теоретического определения среднего дополнительного сопротивления следует применять энергетический подход, свободный от гипотезы проницаемости. Соответствующие зависимости были предложены в 1970-х г.г. И. Герритсмой [] и Н.Н. Юрковым [].Кроме того, для расчёта дополнительного сопротивления возможно применение и полуэмпирического подхода, аналогичного описанному в главе 6 расчёту относительных перемещений от продольной качки. В этом случае также производится двойное нормирование (но уже не передаточной функции, а оператора дополнительного сопротивления) по максимальной ординате и по отвечающей ей частоте, и выполняется аппроксимация дважды нормированногог оператора с таким расчётом, чтобы несобственный интеграл по частотам мог бы быть взят в конечном виде. Соответствующая расчётная схема предложена в 1977 г. В.Б. Липисом, [].Схему И. Герритсма мы рассмотрим в данном разделе, а схему В.Б. Липиса-в следующем разделе.

Отметим, что полное дополнительное сопротивление движению корабля из-за волнения включает, кроме средней не зависящей от времени составляющей, ещё и пульсационную составляющую, которая является гармонической функцией времени и представляет собой ординату возмущающей силы при продольно-горизонтальной качке, [].

Однако на практике учёт пульсационной составляющей дополнительного сопротивления на волнении необходим только при анализе динамики системы корпус – движитель - двигатель, тогда как влияние этой величины на осреднённые за время перехода потери скорости на волнении мало существенно – важным здесь оказывается только среднее дополнительное сопротивление. Поэтому пульсационная составляющая дополнительного сопротивления далее не рассматривается.

В основе алгоритма теоретического расчёта дополнительного сопротивления на волнении лежит допущение о том, что дополнительное сопротивление в характерном для быстроходных водоизмещающих кораблей скоростном режиме на волнении определяется продольной качкой. Тогда в соответствии с выводами линейной гидродинамической теории качки для регулярного волнения с частотой и с длиной , энергия , излучаемая качающимся кораблём за интервал времени, равный кажущемуся периоду волнения 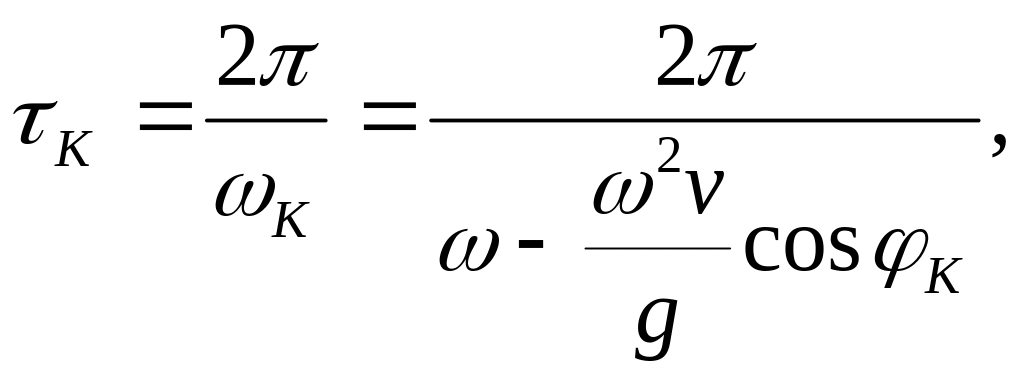должна быть равна работе дополнительного сопротивления на регулярном волнении за тот же интервал времени. Здесь - кажущаяся частота и - курсовой угол корабля по отношению к направлению бега волн. Для встречного волнения и .

Величины и определяются в виде:

;

где , - фазовая скорость волн и волновое число;

- коэффициент демпфирования и присоединённая масса при вертикальных колебаниях шпангоутного контура в сечении с абсциссой ;

- ордината скорости перемещений от продольной качки относительно невозмущённой волны для того же контура;

- ордината КВЛ в сечении с абсциссой х;

- коэффициент полноты погруженной части шпангоутного контура в сечении с абсциссой х;

- безразмерный коэффициент волнового демпфирования вертикальных колебаний по А.З. Салькаеву в сечении с абсциссой х, определяемый по формуле, аналогичной (2.26);

- поправочный коэффициент к присоединённой массе при вертикальных колебаниях эллиптического контура в безграничной жидкости на фактическое отличие шпангоутного контура от полуэллипса, определяется по формуле, аналогичной (2.28);

- поправочный коэффициент к присоединённой массе при вертикальных колебаниях шпангоутного контура в безграничной жидкости на наличие свободной поверхности, определяемый по формуле, аналогичной (2.29).

Тогда из условия выражаем в явном виде дополнительное сопротивление воды движению корабля на регулярном волнении, после чего приходим к формуле И. Герритсма, []:

_где -амплитудное значение скорости перемещений от продольной качки относительно невозмущённой волны для шпангоутного контура в сечении с абсциссой ;

- максимальная ордината амплитудно-частотной характеристики скоростей относительных перемещений в сечении с абсциссой х;

- максимальная ордината амплитудно-частотной характеристики относительных перемещений в сечении с абсциссой х.

Нетрудно видеть, что определённая таким образом величина может быть представлена в виде

,

где оператор дополнительного сопротивления будет