Задания

Задание 1. Решить однородную систему линейных алгебраических уравнений. Указать общее решение системы и фундаментальный набор решений.

1.1.

1.2.

1.3.

1.4.

1.5.

1.6.

1.7.

1.8.

1.9.

1.10.

Задание 2. Найти фундаментальный набор решений однородной системы линейных уравнений.

2.1.

2.2.

2.3.

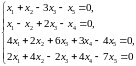
2.4.

2.5.

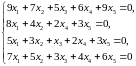
2.6.

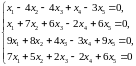
2.7.

2.8.

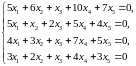
2.9.

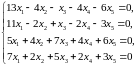
2.10.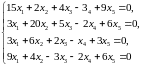

Задание 3. Найти общее решение системы линейных уравнений методом Гаусса, выделив базисные неизвестные, и одно частное решение.

3.1.

3.2.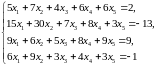

3.3.

3.4.

3.5.

3.6.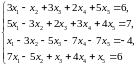

3.7.

3.8.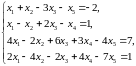

3.9.

3.10.

Методика и порядок выполнения работы

Пример 1

Решить однородную систему линейных алгебраических уравнений. Указать общее решение системы и фундаментальный набор решений.

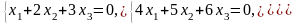
Решение

×(-4) ×(-7)

С помощью элементарных преобразований приведем матрицу системы к ступенчатому виду:

+

+

+

~ ~ ~ .

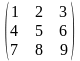
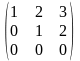Из последней ступенчатой системы видно, что ранг матрицы системы равен 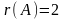, а количество переменных равно , так как , то система неопределенна.

Количество базисных переменных равно . В качестве главных переменных можно выбрать и , соответствующие столбцам ненулевого минора второго порядка: , в качестве свободной переменной – .

Запишем систему, соответствующую полученной матрице:

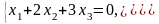
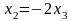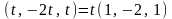Из второго уравнения выражаем через , получим: . Подставляя это выражение в первое уравнение, получим: . Обозначив , получим общее решение системы . это решение можно записать в виде: . Фундаментальную систему решений образует решение .

Пример 2

Найти фундаментальный набор решений однородной системы линейных уравнений.

Решение

×(-3) ×(-4) ×(-3)

С помощью элементарных преобразований приведем матрицу системы к ступенчатому виду:

+

+

+

×(-1)

×(-1/3)

×(1/2)

~ ~

~

×(-1) ×(-1)

+

+

~ .

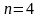Из последней ступенчатой системы видно, что ранг матрицы системы равен , а количество переменных равно , так как , то система неопределенна.

Количество базисных переменных равно 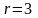. В качестве главных переменных можно выбрать , и , соответствующие столбцам ненулевого минора третьего порядка: , в качестве свободной переменной – .

Запишем систему, соответствующую полученной матрице:

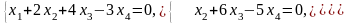
Из третьего уравнения получим: . Подставляя это выражение в первое и второе уравнения, получим: , 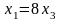. Обозначив , получим общее решение системы . это решение можно записать в виде: . Фундаментальную систему решений образует решение .

Пример 3

Найти общее решение системы линейных уравнений методом Гаусса, выделив базисные неизвестные, и одно частное решение.

Решение

Проведем элементарные преобразование расширенной матрицы системы по методу Гаусса:

×(-2) ×(-2) ×(-3)

+

+

+

~

×1 ×(-1)

+

+

~ ~

~ .

Из последней ступенчатой системы видно, что ранг матрицы системы равен , ранг расширенной матрицы равен , а количество переменных равно , так как , то система совместна и неопределенна.

Количество базисных переменных равно . В качестве главных переменных можно выбрать , и , соответствующие столбцам ненулевого минора третьего порядка: , в качестве свободных переменных – и .

Запишем систему, соответствующую полученной матрице:

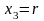Из третьего уравнения выражаем через , получим: . Подставляя это выражение во второе уравнение, получим: . Подставляя выражения для и в первое уравнение, получим: . Обозначив , а получим общее решение системы

Придавая свободным переменным любые значения, будем получать частные решения системы. Частным решением системы будет являться решение .