Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кубанский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Савчук Лин.алгебра для самост. р-ты. 2012.docx

Скачиваний:

Добавлен:

01.07.2025

Размер:

370.79 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Раздел 2. Системы линейных уравнений

Вопросы для подготовки к коллоквиуму

Общий вид системы m линейных уравнений с n переменными (пояснить все обозначения). Решение системы. Совместная система уравнений. Определенная система уравнений. Равносильные системы уравнений.
Несовместная система уравнений. Неопределенная система уравнений Матричная форма записи системы m линейных уравнений с n переменными.
Системы n линейных уравнений с n переменными. Метод обратной матрицы. Теорема Крамера.
Метод Гаусса.
Теорема Кронекера-Капелли. Схема решений системы m линейных уравнений с n переменными. Определение основных, неосновных и базисных переменных.
Системы линейных однородных уравнений. Свойства решений СЛОУ.
Фундаментальная система решений. Теорема о ФСР СЛОУ. Алгоритм нахождения ФСР.
Балансовые соотношения.
Модель Леонтьева многоотраслевой экономики.

Задания для аудиторной самостоятельной работы

1. Решите системы уравнений матричным методом и методом Крамера.

1). 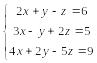2). ; 3). .

2. Решите систему методом Гаусса. Укажите общее и частное решение.

1). 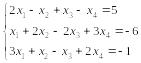2).

3. Найдите все базисные решения системы уравнений

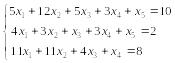
4. Найдите общее решение и фундаментальную систему решений системы линейных однородных уравнений

1). 2).

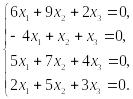
Индивидуальное домашнее задание

Задание № 1.

Проверить совместность системы уравнений и в случае совместности решить ее А) по формулам Крамера; Б) методом обратной матрицы; В) методом Гаусса.

Вариант		1	2	3
Системы	1	2х₁ + х₂ + 3х₃ = 7 2х₁+ 3х₂ + х₃ = 1 3х₁ +2х₂ + х₃ = 6	2х₁ – х₂ +2х₃ = 3 х₁ + х₂ + 2х₃ = -4 4х₁ + х₂ + 4х₃ = -3	3х₁ – х₂ + х₃ = 12 х₁ + 2х₂ + 4х₃ = 6 5х₁ + х₂ + 2х₃ = 3
Системы	2	3х₁+2х₂-4х₃=8 2х₁+4х₂-5х₃=11 х₁-2х₂+х₃=1	х₁+х₂+х₃=1 х₁-х₂+2х₃=-5 2х₁+3х₃=-2	2х₁-х₂+4х₃=15 3х₁-х₂+х₃=8 5х₁-2х₂+5х₃=0
Вариант		4	5	6
Системы	1	2х₁ – х₂ + 3х₃ = -4 х₁ + 3х₂ – х₃ = 11 х₁ – 2х₂ + 2х₃ = -7	3х₁– 2х₂+ 4х₃=12 3х₁+ 4х₂- 2х₃=6 2х₁- х₂- х₃= - 9	8х ₁+ 3х₂- 6х₃=-4 х₁+ х₂- х₃= 2 4х₁+ х₂- 3х₃=-5
Системы	2	3х₁-3х₂+2х₃=2 4х₁-5х₂+2х₃=1 х₁-2х₂=5	3х₁+2х₂-4х₃=8 2х₁+4х₂-5х₃=1 5х₁+6х₂-9х₃=2	3х₁+х₂+2х₃=-3 2х₁+2х₂+5х₃=5 5х₁+3х₂+7х₃=1
Вариант		7	8	9
Системы	1	4х₁+ х₂- 3х₃= 9 х₁+ х₂- х₃= -2 8х₁+ 3х₂- 6х₃=12	2х₁+3х₂+4х₃=33 7х₁-5х₂=24 4х₁+11х₃=39	2х₁+3х₂+4х₃=12 7х₁-5х₂+х₃=-33 4х₁+х₃=-7
Системы	2	4х₁-7х₂-2х₃=0 2х₁-3х₂-4х₃=6 2х₁-4х₂+2х₃=2	5х₁-9х₂-4х₃=6 х₁-7х₂-5х₃=1 4х₁-2х₂+х₃=2	х₁-5х₂+х₃=3 3х₁+2х₂-х₃=7 4х₁-3х₂=1
Вариант		10	11	12
Системы	1	х₁+4х₂-х₃=6 5х₂+4х₃=-20 3х₁-2х₂+5х₃=-22	3х₁-2х₂+4х₃=21 3х₁+4х₂-2х₃=9 2х₁-х₂-х₃=10	3х₁-2х₂-5х₃=5 2х₁+3х₂-4х₃=12 х₁-2х₂+3х₃=-1
Системы	2	5х₁-5х₂-4х₃=-3 х₁-х₂+5х₃=1 4х₁-4х₂-9х₃=0	7х₁-2х₂-х₃=2 6х₁-4х₂-5х₃=3 х₁+2х₂+4х₃=5	4х₁-3х₂+х₃=3 х₁+х₂-х₃=4 3х₁-4х₂+2х₃=2
Вариант		13	14	15
Системы	1	4х₁+х₂+4х₃=19 2х₁-х₂+2х₃=11 х₁+х₂+2х₃=8	2х₁-х₂+2х₃=0 4х₁+х₂+4х₃=6 х₁+х₂+2х₃=4	2х₁-х₂+2х₃=8 х₁+х₂+2х₃=11 4х₁+х₂+4х₃=22
Системы	2	3х₁+х₂+2х₃=1 2х₁+2х₂-3х₃=9 х₁-х₂+х₃=2	6х₁+3х₂-5х₃=0 9х₁+4х₂-7х₃=3 3х₁+х₂-2х₃=5	8х₁-х₂+3х₃=2 4х₁+х₂+6х₃=1 4х₁-2х₂-3х₃=7
Вариант		16	17	18
Системы	1	2х₁-х₂-3х₃=-9 х₁+5х₂+х₃=20 3х₁+4х₂+2х₃=15	2х₁-х₂-3х₃=0 3х₁+4х₂+2х₃=1 х₁+5х₂+х₃=-3	-3х₁+5х₂+6х₃=-8 3х₁+х₂+х₃=-4 х₁-4х₂-2х₃=-9
Системы	2	2х₁+3х₂+4х₃=5 х₁+х₂+5х₃=6 3х₁+4х₂+9х₃=0	2х₁-3х₂-4х₃=1 7х₁-9х₂-х₃=3 5х₁-6х₂+3х₃=7	5х₁+6х₂-2х₃=2 2х₁+3х₂-х₃=9 3х₁+3х₂-х₃=1
Вариант		19	20	21
Системы	1	3х₁+х₂+х₃=-4 -3х₁+5х₂+6х₃=36 х₁-4х₂-2х₃=-19	3х₁-х₂+х₃=-11 5х₁+х₂+2х₃=8 х₁+2х₂+4х₃=16	3х₁-х₂+х₃=9 5х₁+х₂+2х₃=11 х₁+2х₂+4х₃=19
Системы	2	3х₁+х₂-2х₃=6 5х₁-3х₂+2х₃=4 -2х₁+5х₂-4х₃=0	2х₁+х₂+х₃=2 5х₁+х₂+3х₃=4 7х₁+2х₂+4х₃=1	х₁-2х₂-3х₃=3 х₁+3х₂-5х₃=0 2х₁+х₂-8х₃=4
Вариант		22	23	24
Системы	1	2х₁+3х₂+х₃=4 2х₁+х₂+3х₃=0 3х₁+2х₂+х₃=1	2х₁+3х₂+х₃=12 2х₁+х₂+3х₃=16 3х₁+2х₂+х₃=8	х₁-2х₂+3х₃=14 2х₁+3х₂-4х₃=-16 3х₁-2х₂-5х₃=-8
Системы	2	х₁-4х₂-2х₃=0 3х₁-5х₂-6х₃=2 4х₁-9х₂-8х₃=1	4х₁+х₂-3х₃=1 3х₁+х₂-х₃=2 х₁-2х₃=5	3х₁-5х₂+3х₃=4 х₁+2х₂+х₃=8 2х₁-7х₂+2х₃=1
Вариант		25	26	27
Системы	1	3х₁+4х₂-2х₃=11 2х₁-х₂-х₃=4 3х₁-2х₂+4х₃=11	х₁+5х₂-6х₃=-15 3х₁+х₂+4х₃=13 2х₁-3х₂+х₃=9	4х₁-х₂=-6 3х₁+2х₂+5х₃=-14 х₁-3х₂+4х₃=-19
Системы	2	х₁-2х₂+3х₃=6 2х₁+3х₂-4х₃=2 3х₁+х₂-х₃=5	5х₁-х₂-2х₃=1 3х₁-4х₂+х₃=7 2х₁+3х₂-3х₃=4	2х₁+8х₂-7х₃=0 2х₁-5х₂+6х₃=1 4х₁+3х₂-х₃=7
Вариант		28	29	30
Системы	1	5х₁+2х₂-4х₃= -16 х₁+3х₃= -6 2х₁-3х₂+х₃=9	х₁+4х₂-х₃=-9 4х₁-х₂+5х₃=-2 3х₂-7х₃=-6	7х₁+4х₂-х₃=13 3х₁+2х₂+3х₃=3 2х₁-3х₂+х₃=-10
Системы	2	3х₁+4х₂+х₃=2 х₁+5х₂-3х₃=4 2х₁-х₂+4х₃=5	2х₁-3х₂+2х₃=5 3х₁+4х₂-7х₃=2 5х₁+х₂-5х₃=9	4х₁-9х₂+5х₃=1 7х₁-4х₂+х₃=11 3х₁+5х₂-4х₃=5

Задание № 2. Найти фундаментальную систему решений однородной системы линейных уравнений.

Задание № 3.

Исследовать и решить систему уравнений методом Гаусса.

Вариант				1		2			3
Системы	12х₁+х₂=1 х₂+2х₃+х₄=9 4х₁-17х₂-6х₃-5х₄=-17					7х₁-6х₂+2х₃=2 2х₁-7х₂-2х₃-х₄=-4 2х₁-9х₂-4х₃-3х₄= -6			2х₁-2х₂+х₄=15 5х₁+5х₂=43 9х₁+4х₂+5х₃+7х₄=53
Вариант					4		5			6
Системы		2х₁-9х₂-4х₃-3х₄= -6 2х₁-7х₂-2х₃-х₄= -4 7х₁-6х₂+2х₃=2 7х₁-17х₂+х₃-2х₄=14				8х₁-х₂-х₃+3х₄=30 5х₁-5х₂-х₃-2х₄=1 10х₁+3х₂+2х₄=51 3х₁+2х₂+х₄=19			3х₁-3х₂-4х₃+х₄=1 х₂+5х₃+х₄=-12 5х₂-14х₃+3х₄= -46
Вариант				7		8			9
Системы	х₁+5х₂-2х₃=9 2х₁-7х₂-х₄= -14 2х₁-10х₂-4х₄= -26					3х₁+2х₂+х₄=17 х₁+2х₂-х₃= - 4 5х₁+х₂-8х₃+2х₄=16			4х₁-7х₂+14х₃+5х₄=-5 х₁+2х₂-3х₃-х₄=15 3х₁-х₂=13
Вариант			13					14			15
Системы		3х₁-7х₂+7х₃+2х₄=8 х₁+8х₂+10х₃+3х₄=3 4х₁-2х₂+3х₃+х₄=17 5х₁-17х₂+х₃-2х₄=-24						3х₁-х₂+2х₃+5х₄= -1 3х₁-3х₂+6х₃+15х₄=-3 3х₁-х₂+3х₃+14х₄= -8			2х₁+7х₂+3х₃+х₄=6 5х₁+12х₂+5х₃+3х₄=10 6х₁-х₂-2х₃+5х₄=-2

Вариант

Системы

2х₁+3х₂-5х₃=7

6х₁+8х₂-14х₃=17

2х₁-2х₂-х₃=1

5х₁+11х₂-16х₃=21

2х₁-5х₂+3х₃+х₄=5

3х₁-7х₂+3х₃-х₄= -1

5х₁-9х₂+6х₃+2х₄=7

4х₁-6х₂+3х₃+х₄=8

2х₁+3х₂+11х₃+5х₄=5

х₁+х₂+5х₃+2х₄=3

3х₁+2х₂+8х₃+4х₄=5

Вариант		16	17	18
Системы	8х₁-х₂+3х₃=22 4х₁+х₂+6х₃= -1 13х₁+х₂+16х₃=5		5х₁-5х₂-4х₃= -3 х₁-х₂+5х₃=11 4х₁-3х₂-6х₃= -9	2х₁+3х₂+х₃-2х₄=29 3х₁+х₂+4х₃+5х₄=26 7х₁+8х₂+2х₃+17х₄=64
Вариант		19	20	21
Системы	3х₁+х₂+2х₃+3х₄=16 2х₁-2х₂+х₃=15 5х₁+5х₂+х₃=15		2х₁+х₂+2х₄=22 8х₁-2х₂+5х₄=23 26х₁+х₂-2х₃-5х₄=-39	8х₁-2х₃+5х₄=23 26х₁+х₂-2х₃-5х₄=-39 4х₁-2х₂-х₃-6х₄=-64
Вариант		22	23	24
Системы	х₁+5х₃+х₄= -12 5х₂+14х₃+3х₄= -46 3х₁-3х₂-4х₃+х₄=1		3х₁-3х₂-4х₃+х₄=1 х₁-8х₂-7х₃-2х₄=45 5х₂+14х₃+3х₄=-46	2х₁-4х₂+2х₃+х₄=-23 10х₁-9х₂+7х₃-5х₄=-31 10х₂+2х₄=96
Вариант		25	26	27
Системы	х₁+2х₂+3х₃+х₄=1 3х₁+13х₂+13х₃+5х₄=3 х₁+5х₂+3х₃+х₄=7		2х₁-х₂+3х₃=0 -2х₁+3х₂-х₄=1 х₂-3х₃+4х₄=-1	-х₂+3х₃-4х₄=2 2х₁+6х₃-4х₄=3 -х₁+2х₂+х₃-3х₄=0

Вариант

Системы

2х₁+3х₂+4х₃+х₄=2

х₁+х₂+7х₃+х₄=6

3х₁+2х₂+х₃+5х₄=8

х₁-2х₂-х₃+3х₄=5

2х₁-4х₂-2х₃+6х₄=10

2х₁+х₂+х₄=20

3х₁-7х₂+7х₃+2х₄=8

х₁-8х₂+10х₃+3х₄=9

5х₁-17х₂+х₃-2х₄=-24

Задание № 4.

Найти все базисные решения систем уравнений.

Вариант							1					2			3					4
Система			х₁+2х₂=1 -х₂+х₄+х₅=4 3х₁-х₃+2х₅=2									2х₁+3х₂+х₄=6 х₂-х₃=4 -3х₁-х₃-х₅=2			2х₁-х₃-х₄=4 х₂+3х₃+2х₄=3					2х₁+х₃= -5 -х₁+х₂=3 3х₁-х₄=1
Вариант						5			6								7					8
Система		х₁+2х₄-2х₅=4 -х₃-3х₄+х₅=5 х₂+3х₅= -2							х₁+х₂+х₃+х₄+х₅=5 х₁-х₂+х₃-х₄+х₅=1								х₁-2х₂+х₃+х₄=1 х₁-2х₂+х₃-х₄= -1					х₁-2х₂+х₃-х₄=-1 х₁-2х₂+х₃+5х₄=5
Вариант						9			10								11					12
Система		х₁+х₂+х₃+х₄=4 -х₁+х₂+х₃+х₄=3							х₁+х₂+х₃+х₄+х₅=1 х₁+х₃+2х₅=4								х₁-2х₂+х₃+х₄=1 х₁-2х₂+х₃+5х_4 =5					х₁-х₂+х₃+х₄=4 х₁-х₂+х₃-2х₄=0
Вариант				13							14			15					16
Система	х₁+2х₂+2х₃+х₄=2 2х₁+х₂+х₃-2х₄=6									х₁+х₄=2 х₁+х₂+х₃=3			х₁+х₂+х₃+х₄+х₅=1 х₁+х₃+2х₅=4 х₂+х₄= -2					х₁+х₂+х₃-х₄+х₅=5 х₁+х₃+2х₅=4 х₂-х₄=0
Вариант					17			18								19					20
Система		6х₁+3х₂+4х₃-3х₄+4х₅=5 4х₁+2х₂+х₃-2х₄+3х₅=4							х₁-2х₂+3х₃₊ +2х₄+х₅=4 3х₁-6х₂+5х₃ +4х₄+3х₅=5								4х₁+2х₂+3х₃-2х₄+4х₅=0 6х₁+3х₂+2х₃-3х₄+4х₅=5					х₁-2х₂+7х₃+4х₄+х₅=11 х₁-2х₂+3х₃+2х₄+х₅=4

Вариант

Система

2х₁-х₂-х₃+2х₄+3х₅=2

6х₁-3х₂-2х₃+4х₄+5х₅=3

6х₁-3х₂-4х₃+8х₄+13х₅ = 9

2х₁-х₂-х₃+2х₄+3х₅=2

х₁+х₂+х₃+х₄=1

х₂+х₃+х₄=1

х₃+х₄=1

-х₁-2х₂+х₃+х₄=1

-2х₁+х₂+х₃++х₄=2

3х₁+2х₄=3

Вариант

Система

х₁+2х₂-х₃+х₄=3

х₁+4х₂+х₃= -2

2х₁+х₂-х₃+х₄=3

-2х₁+х₂+х₃-х₄= -1

х₁+х₂+х₃+х₄+х₅=5

х₂+х₃+х₄-х₅=2

х₃-х₄+х₅=1

х₁+х₂+х₃+5х₄=0

х₁+х₂-х₄=3

х₁-х₂+3х₄= -1

Вариант

Система

х₁+х₂+х₃+2х₄=7

х₂+х₃+х₄=5

х₁-х₄=3

х₁+2х₂-х₄=3

х₁-х₂+3х₄= -1

2х₁+х₂+х₃-х₄=5

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.09.201968.07 Кб3С 1-13.docx
#
12.09.2019121.91 Кб1С 14.docx
#
01.03.2025275.19 Кб0с 46-54.rtf
#
16.09.2019124.54 Кб22с ответами ПСИХОЛОГИЯ РАЗВИТИЯ.docx
#
09.05.2015238.03 Кб204с ответами.rtf
#
01.07.2025370.79 Кб0Савчук Лин.алгебра для самост. р-ты. 2012.docx
#
01.04.2025207.36 Кб0Сам.раб.РЭАИС.DOC
#
06.09.201982.94 Кб4самомассаж.doc
#
01.05.20254.8 Mб0Самоучитель по OrCAD.docx
#
09.05.2015267.01 Кб5самохин вопросы.pdf
#
09.05.20152.1 Mб32Сборник девиантологических статей.pdf