Лекция 18. Подобие тепловых процессов

18.1. Тепловое подобие

Из уравнения Фурье – Кирхгофа следует, что температурное поле в движущейся жидкости является функцией различных переменных, в том числе скорости и плотности жидкости. Поэтому для практического использования уравнение (17.7) подобно преобразовывают с учетом условий однозначности, т. е. представляют в виде функции от критериев подобия.

Рассмотрим первоначально подобие граничных условий. Как указывалось, при турбулентном движении жидкости тепло у границы потока, т. е. в непосредственной близости от твердой стенки, передается теплопроводностью через пограничный слой в направлении, перпендикулярном направлению движения потока. Следовательно, по закону Фурье, уравнение (15.11), количество тепла, проходящее в пограничном слое толщиной через площадь сечения dF за время , составляет

(А)

Количество тепла, проходящее от стенки в ядро потока, определяется по уравнению теплоотдачи (17.3):

(Б)

При установившемся процессе теплообмена количества тепла, проходящие через пограничный слой и ядро потока, равны. Поэтому, приравнивая выражения (А) и (Б) и сокращая подобные члены, получим

= (18.1)

Для подобного преобразования этого уравнения разделим его правую часть на левую и отбросим знаки математических операторов. При этом величину заменим некоторым определяющим геометрическим размером . Тогда получим безразмерный комплекс величии

(18.2)

который называется критерием Нуссельта. Равенство критериев Нуссельта характеризует подобие процессов теплопереноса на границе между стенкой и потоком жидкости. На основе совместного рассмотрения уравнений (А) и (Б) можно показать, что Nu является мерой соотношения толщины пограничного слоя и определяющего геометрического размера (для трубы – ее диаметр d).

В критерий Нуссельта входит обычно определяемая в задачах по конвективному теплообмену величина коэффициента теплоотдачи .

Теперь рассмотрим условия подобия в ядре потока, используя подобное преобразование уравнения (17.7). В левой части уравнения Фурье – Кирхгофа сумма членов, отражающих влияние скорости потока на теплообмен, может быть заменена величиной:

где l – определяющий линейный размер.

Правую часть того же уравнения, характеризующую перенос тепла путем теплопроводности, также заменим величиной:

Член , отражающий неустановившийся режим теплообмена, может быть заменен отношением . Выразим все члены уравнения (17.7) в относительных единицах, приняв за масштаб количество тепла, передаваемого путем теплопроводности.

Разделив член на , получим безразмерный комплекс величин . Этот комплекс обычно заменяют на обратную величину с тем, чтобы в расчетах нe оперировать с дробными числами. Последний комплекс носит название критерия Фурье:

(18.3)

Равенство критериев Фурье в сходственных точках тепловых потоков – необходимое условие подобия неустановившихся процессов теплообмена.

Критерий Фурье является аналогом критерия гомохронности Но при гидродинамическом подобии.

Разделив конвективный член на и произведя необходимые со­кращения, получим

(18.4)

Этот безразмерный комплекс величин называется критерием Пекле. Он» как следует из проведенного подобного преобразования, является мерой соотношения между теплом, переносимым путем конвекции и теплопроводности при конвективном теплообмене.

Необходимыми условиями подобия процессов переноса тепла является, кроме того, соблюдение гидродинамического и геометрического подобия. Первое характеризуется равенством критериев Но, Re и Fr в сходственных точках подобных потоков, а второе – постоянством отношения основных геометрических размеров стенки L₁, L₂, ..., L_n к некоторому характерному размеру.

Для труб характерным размером обычно является их диаметр (L₀ = d). В качестве L₀ могут быть приняты также длина трубы, радиус кривизны изогнутой трубы и т. д.

Таким образом, обобщенное (критериальное) уравнение конвективного теплообмена выражается функцией вида

(18.5)

или с учетом того, что критерий Нуссельта является определяемым, так как в него входит искомая величина коэффициента теплоотдачи

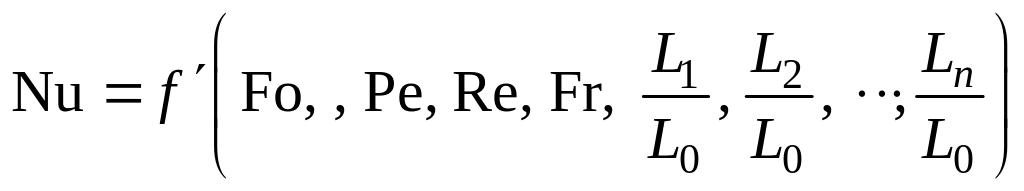(18.6)

Критерий Пекле может быть представлен как произведение двух без­размерных комплексов:

Безразмерный комплекс

(18.7)

называется критерием Прандтля. Он целиком составлен из величин, выражающих физические свойства жидкости, и характеризует подобие физических свойств теплоносителей в процессах конвективного теплообмена. Критерий Рг является мерой подобия полей температур и скоростей.

Значения критерия Прандтля для капельных жидкостей порядка 3—300 и значительно уменьшаются с возрастанием температуры, а для газов постоянны и зависят от атомности газа (Рг ~ 0,7 ÷ 1). Поэтому для жидкостей тепловой подслой тоньше гидродинамического.

С введением критерия Рг обобщенное уравнение конвективного тепло­обмена принимает вид

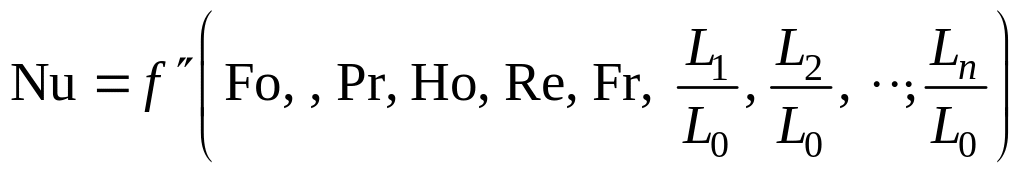(18.8)

При установившемся процессе теплообмена из обобщенного уравнения исключаются критерии Fo и Но. При вынужденном движении, когда влияние сил тяжести на гидродинамику потока, отдающего или воспринимающего тепло, пренебрежимо мало, влиянием критерия Fr на теплоотдачу можно пренебречь. Тогда

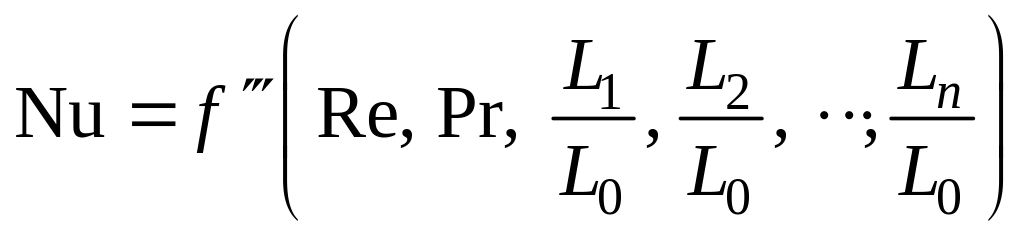(18.9)

Вид функций (18.8) и (18.9) определяется опытным путем, причем обычно им придают степенную форму. Так, например, уравнение (18.9) при движении потока в трубе диаметром d и длиной l может быть представлено в виде

(18.10)

где С, m, n, p – величины, определяемые из опыта.

При теплоотдаче в условиях естественной конвекции в число определяющих критериев должен войти критерий Фруда, отражающий действие сил тяжести в подобных потоках (Fr = w²/gl). Однако в виду трудности определения скорости при естественной конвекции критерий Фруда целесообразно заменить для данных условий на производный критерий Архимеда.

(18.11)

Рисунок 18.1 – Нагревание жидкости в условиях естественной циркуляции

Когда процесс теплообмена протекает в условиях естественной конвекции, т е свободного движения, обусловленного разностью плотностей нагретых и холодных элементарных объемов жидкости, их разность плотностей и подъемная сила, возникающая при движении частиц, определяются температурным напором Поэтому величину можно заменить пропорциональной величиной .

Если неподвижная жидкость нагревается в аппарате без принудительного перемешивания (рис. 18.1), то для любых двух частиц, находящихся на различном расстоянии от стенки, через которую передается тепло, t > t₀ и , причем . Следовательно, зависимость между движущей силой естественной конвекции, определяемой разностью плотностей , и ее выражением через разность температур имеет вид

Подставляя в критерий Аr значение и сокращая получаем выражение нового критерия – критерия Грасгофа:

(18.12)

где – коэффициент объемного расширения жидкости, 1/К; – разность температур между стенкой и жидкостью (или наоборот), которой определяется разность плотностей жидкости, К; l – определяющий геометрический размер (для трубы – ее диаметр, для вертикальной плоской стенки – ее высота)

Таким образом, критерий Gr является, подобно критериям Галилея (Ga) и Архимеда (Аr), аналогом критерия Фруда. Критерий Gr представляет собой определяющий критерий теплового подобия при естественной конвекции, когда движение жидкости целиком обусловлено самим процессом теплообмена Критерий Грасгофа можно рассматривать как меру отношения сил трения к подъемной силе, определяемой разностью плотностей в различных точках неизотермического потока.

Следовательно, для процессов теплоотдачи при естественной конвекции, или свободном движении жидкости, обобщенное уравнение теплоотдачи может быть представлено в виде

(18.13)

Для газов и, значит, критерий Рr можно исключить из обобщенных уравнений для определения коэффициента теплоотдачи.