ВСТУП

Тестові завдання та приклади їх розв'язання розроблені для студентів денної форми навчання, що вивчають повний курс опір матеріалів.

У методичних вказівках наведено перелік основних теоретичних питань з розділів «Момент інерції плоских фігур», «Міцність при згинанні», «Деформації при згинанні», знаннями з яких повинен володіти студент для успішного складання модульного контролю МК2, а також приклади розв’язання типових тестових завдань з таких тем :

• Момент інерції плоских фігур:

  • теоретичні питання щодо моментів інерції плоских фігур;

  • визначення координат центру ваги фігури;

  • обчислення моментів інерції відносно центральний осей;

  • визначення моментів інерції відносно осей, що проходять через основні розміри фігур в загальному вигляді;

  • обчислення моментів інерції відносно осей, що проходять через основні розміри фігур;

• Міцність при згині:

  • теоретичні питання міцності при згині;

  • визначення опорних реакцій та внутрішніх зусиль в балках;

  • обрати варіант правильно побудованих епюр;

  • визначення нормальних напружень у заданій точці поперечного перерізу;

  • добір перерізу балки при згині.

• Деформації при згинанні:

  • теоретичні питання стосовно деформації при згинанні;

  • порівняння прогинів при різному навантаженні;

  • визначення прогинів за допомогою методу початкових параметрів;

  • визначення переміщень в простих балках.

Розділ I. Моменти інерції плоских фігур.

Теоретичні питання

1. Де розташовано центр ваги прямокутника?

2. Де розташовано центр ваги трикутника?

3. Де розташовано центр ваги кола?

4. Які осі називаються головними?

5. Які осі називаються центральними?

6. Які осі називаються головними центральними?

7. На яких осях будується еліпс інерції?

8. Які значення приймають моменти інерції відносно головних центральних осей?

9. Як називаються вісі, які проходять через центр ваги і хоча б одна з яких збігається з віссю симетрії?

10. Яке значення має відцентровий момент інерції відносно осей, щодо яких осьові моменти інерції мають однакові значення?

11. .За якою формулою визначається статичний момент фігури (див. рис. 1) відносно осі z в загальному вигляді?

    Рис. 1

12. За якою формулою визначається статичний момент фігури (див. рис. 1) відносно осі у в загальному вигляді?

13. За якою формулою визначається осьовий момент фігури (див. рис. 1) відносно осі у в загальному вигляді?

14. За якою формулою визначається осьовий момент фігури (див. рис. 1) відносно осі z в загальному вигляді?

15. За якою формулою визначається відцентровий момент фігури (див. рис. 1) відносно осей у,z в загальному вигляді?

16. Чому дорівнює відцентровий момент інерції відносно головних центральних осей ?

17. За якою формулою визначається полярний момент інерції фігури (див. рис. 2) в загальному вигляді?

Рис. 2

18. За якою формулою визначається полярний момент інерції, якщо відомі осьові моменти інерції?

19. За якою формулою визначається полярний момент інерції кола відносно його центра?

20. За якою формулою визначається осьовий момент інерції кола відносно центральних осей?

21. Чому дорівнює відцентровий момент інерції кола відносно осей, що проходять через центр ваги?

22. Для яких зі схем (див. рис. 3) відцентровий момент інерції дорівнює нулю?

Рис. 3

23. Чому дорівнює статичний момент відносно центральних осей?

24. За якою формулою визначається осьовий момент прямокутника (див. рис. 4) відносно осі У_с в загальному вигляді?

Рис. 4

25. За якою формулою визначається осьовий момент прямокутника (див. рис.4) відносно осі Z_с в загальному вигляді?

26. .За якою формулою визначається осьовий момент трикутника (див. рис. 5) відносно осі У_с в загальному вигляді?

Рис. 5

27. За якою формулою визначається осьовий момент трикутника (див. рис. 5) відносно осі Z_с в загальному вигляді?

28. За якою формулою визначається відцентровий момент трикутника (див. рис. 5) відносно осей Z_сУ_с в загальному вигляді?

29. Для яких із схем (див. рис. 6) відцентровий момент інерції має від’ємне значення?

Рис. 6

Визначення координат центру ваги фігури

1. Визначити координати центру ваги прямокутника z_С, y_С (в см) (див. рис. 7). Відповідь дати в см.

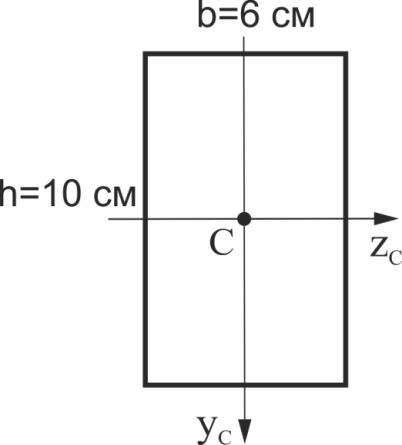
Рис. 7

2. Визначити координати центру ваги прямокутника z_С, y_С (в см) (див. рис. 8). Відповідь дати в см.

Рис. 8

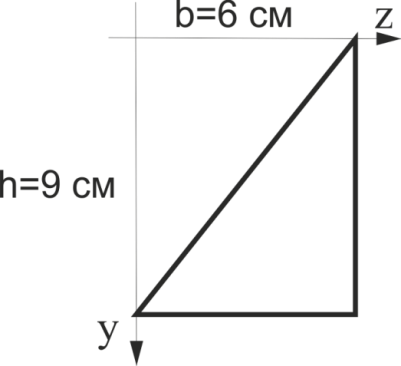
3. Визначити координати центру ваги трикутника z_С, y_С (в см) (див. рис. 9). Відповідь дати в см.

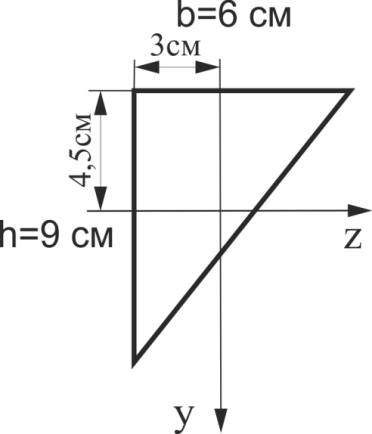
Рис. 9

4. Визначити координати центру ваги трикутника, наведеного на малюнку. Відповідь дати в см (zc, yc).

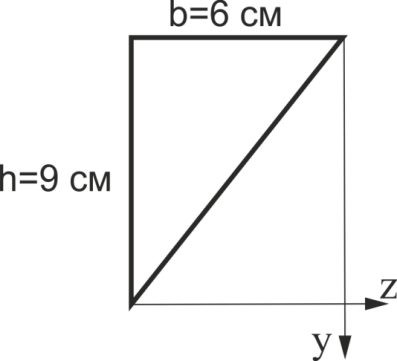
Рис.10

6. Розрахувати координати центру ваги трикутника, наведеного на рис. 11.

   Рис. 11

7. Розрахувати координати центру ваги трикутника, наведеного на на рис. 12.

Рис. 12

6. Визначити координати центра ваги кола, наведеного на рис. 13. Відповідь дати в см (zc, yc)

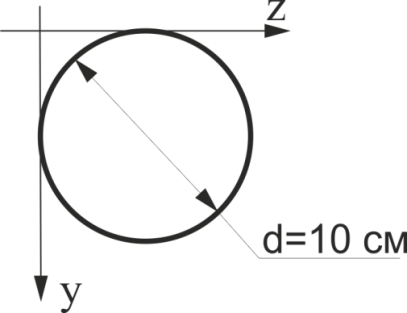
Рис.13

6. Визначити координату у_c центра ваги поперечного перерізу, наведеного на рис. 14. Відповідь дати в см

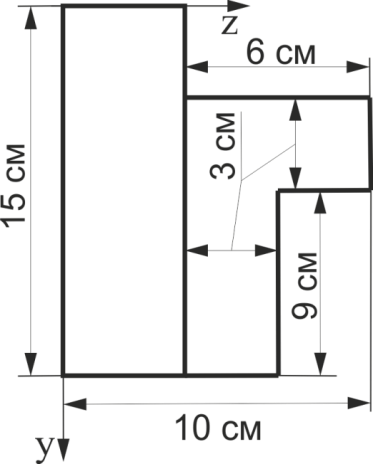
Рис. 14

6. Визначити координату z_c (в см) центру ваги поперечного перерізу рис. 14. Відповідь дати в см

Обчислення моментів інерції відносно центральний осей

1. Обчислити осьовий момент інерції трикутника відносно осі Zс (рис.15). Відповідь надати в см⁴з одним знаком після коми.

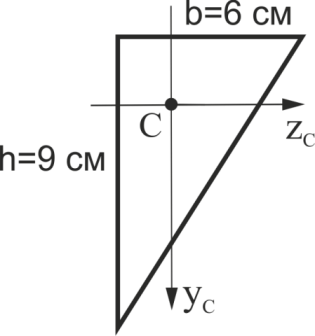
Рис.15

2. Обчислити відцентровий момент інерції трикутника ( рис. 15) щодо осей ZсУс. Відповідь дати в см⁴ з одним знаком після коми.

3. Обчислити осьовий момент інерції трикутника (див. рис.15) щодо осі Ус. Відповідь дати в см⁴ с одним знаком після коми.

4. Обчислити осьовий момент інерції прямокутника щодо осі Zс Відповідь дати в см⁴.

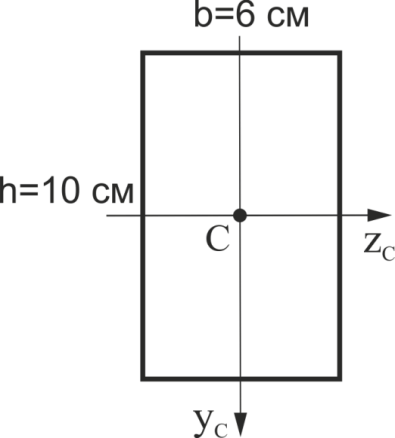
Рис.16

5. Обчислити відцентровий момент інерції прямокутника (див. рис.16) щодо осей ZсУс. Відповідь дати в см⁴.

6. Розрахувати осьовий момент інерції прямокутника (див. рис.16) щодо осі Ус. Відповідь дати в см⁴.

7. Розрахувати відцентровий момент інерції кола щодо осей Z_сУ_с. Відповідь дати в см⁴.

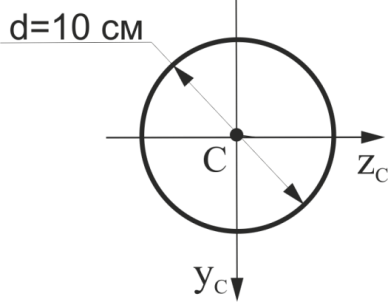
Рис.17.

8. Розрахувати осьовий момент інерції кола(див. рис.17) щодо осі Ус. Відповідь дати в см⁴.

9. Розрахувати осьовий момент інерції прямокутника (див. рис.17) щодо осі Zс. Відповідь дати в см⁴.

10. Розрахувати осьові моменти інерції щодо центральних осей, паралельних основним розмірам для заданої фігури (див. рис.18)

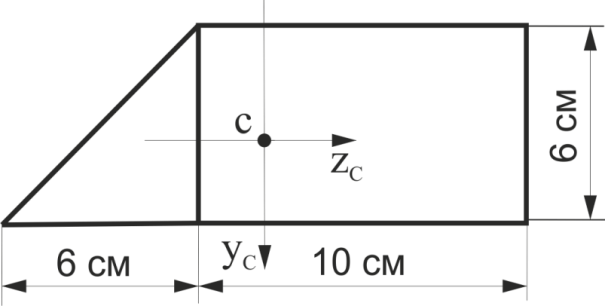
    Рис.18

11. Розрахувати осьові моменти інерції щодо центральних осей, паралельних основним розмірам для заданої фігури (див. рис.19)

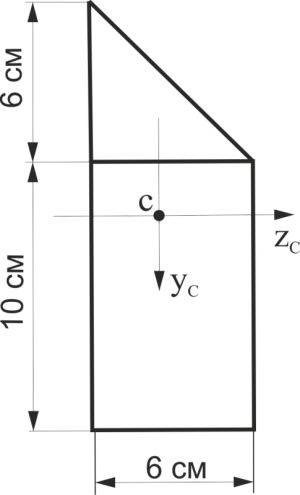
    Рис.19

12. Розрахувати відцентровий момент інерції щодо центральних осей, паралельних основним розмірам для заданої фігури (див. рис.19)

Визначення моментів інерції відносно осей, що проходять через основні розміри фігур в загальному вигляді

1. Визначити в загальному вигляді осьові моменти інерції прямокутника щодо осей У та Z, що проходять через основні розміри (див. рис. 20).

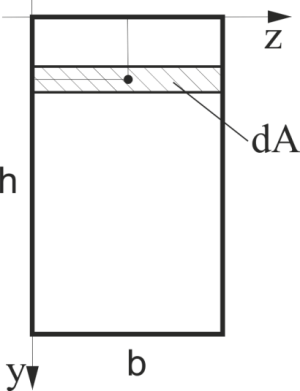
   Рис.20

2. Визначити в загальному вигляді відцентровий момент інерції прямокутника щодо осей УZ, що проходять через основні розміри (див. рис.20).

3. Визначити в загальному вигляді осьові моменти інерції трикутника щодо осей У та Z, що проходять через основні розміри (див. рис.21).

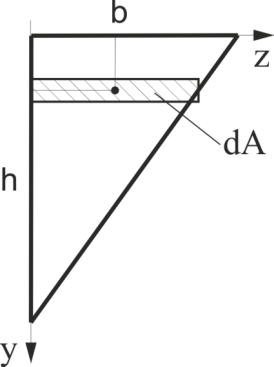
   Рис.21

4. Визначити в загальному вигляді відцентровий момент інерції трикутника щодо осей УZ, що проходять через основні розміри (див. рис.21).

5. Визначити в загальному вигляді осьовий момент інерції прямокутника щодо осі Z (див. рис.22).

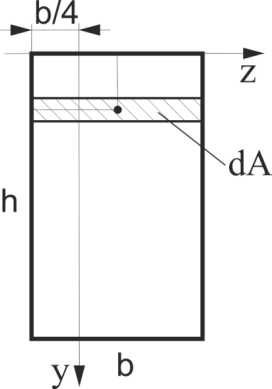
Рис.22

6. Визначити в загальному вигляді відцентровий момент інерції прямокутника щодо осей ZY (див. рис.22).

7. Визначити в загальному вигляді осьовий момент інерції прямокутника щодо осі У (див. рис.22).

8. Розрахувати відцентровий момент інерції кола щодо осей ZУс.

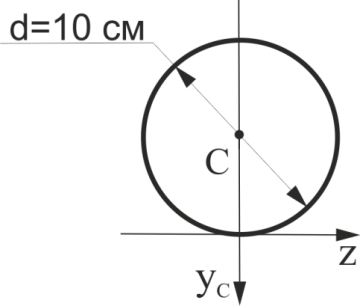
Рис.23

6. Визначити в загальному вигляді осьовий момент інерції кола щодо осі Z(див. рис.23) дорівнює

Обчислення моментів інерції відносно осей, що проходять через основні розміри фігур

1. Обчислити відцентровий момент інерції прямокутника щодо осей ZУ. Відповідь дати в см⁴.

Рис.24

2. Обчислити осьовий момент інерції прямокутника щодо осі Z (див. рис.24). Відповідь дати в см⁴.

3. Обчислити осьовий момент інерції прямокутника щодо осі У (див. рис.24). Відповідь дати в см⁴.

4. Обчислити осьовий момент інерції прямокутника щодо осі Z, якщо

I_zc=1464 см⁴, О – центр ваги. Відповідь дати в см⁴.

Рис.25

5. Обчислити відцентровий момент інерції прямокутника щодо осей ZУ (див. рис.25). Відповідь дати в см⁴.

6. Обчислити осьовий момент інерції прямокутника щодо осі У(див. рис.25), О – центр ваги . Відповідь дати в см⁴.

7. Обчислити осьовий момент інерції трикутника щодо осі Z. Відповідь дати в см⁴.

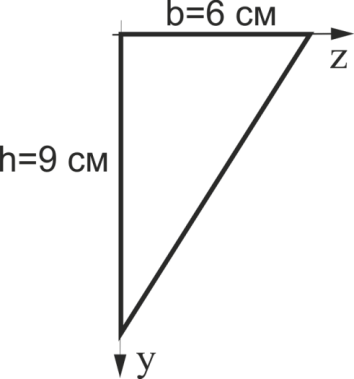
Рис.26

8. Обчислити осьовий момент інерції трикутника щодо осі У(див. рис.26). Відповідь дати в см⁴.

9. Обчислити відцентровий момент інерції трикутника щодо осей ZY(див. рис.26). Відповідь дати в см⁴.

Розділ II. Міцність при згині

Теоретичні питання

1. За якою формулою визначається момент опору для прямокутного перерізу при згині?

2. Який вид деформування називається чистим згинанням?

3. За якою формулою визначається момент опору для круглого перерізу при згині?

4. За якою формулою визначається розрахункове напруження за III-ою теорією міцності?

5. За якою формулою визначається розрахункове напруження за IV –ою теорією міцності?

6. За якою формулою визначаються дотичні напруження при згині?

7. Нормальні напруження при згині визначаються за формулою:

8. За якою формулою визначаються найбільші нормальні напруження при згині ?

9. Записати умову міцності при згині

10. Поперечна сила Q (x) має позитивне значення в поперечному перерізі, якщо вона спрямована

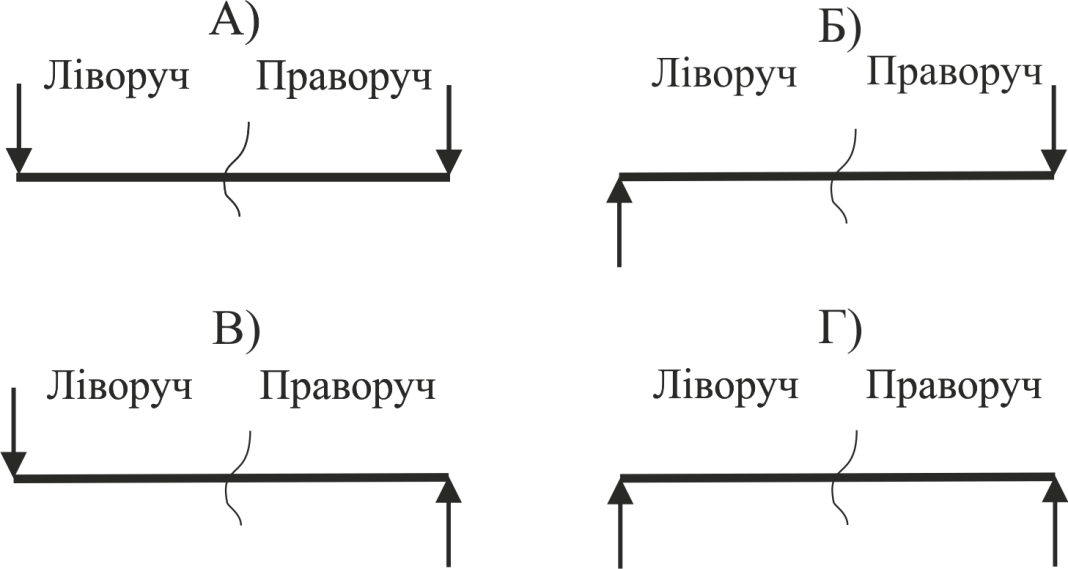
Рис.27

12. Згинаючий момент М(х) має в перерізі додатне значення, якщо він спрямовань

Рис.28

Визначення опорних реакцій та внутрішніх зусиль в балках.

1. Визначити опорні реакції

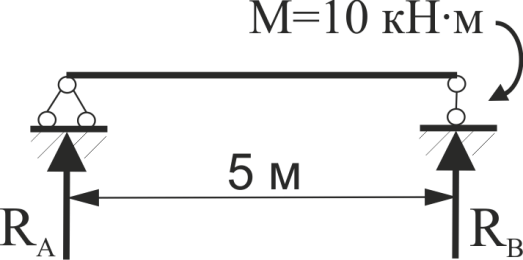
Рис.29.

2. Визначити опорні реакції

Рис.30.

3. Визначити опорні реакції

Рис.31.

4. Визначити опорні реакції

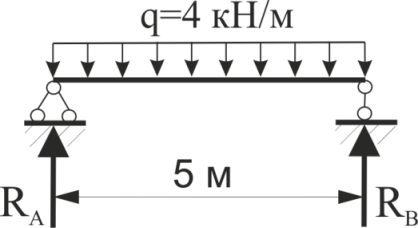
Рис.32.

5. Записати аналітичний вираз згинаючого моменту для перерізу 1-1

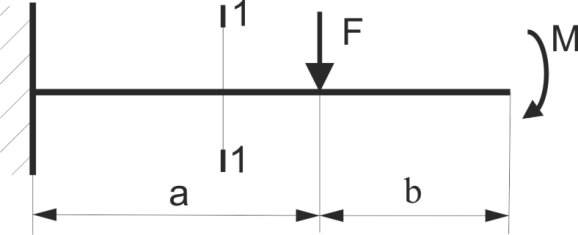
Рис.33

6. Записати аналітичний вираз поперечної сили для перерізу 1-1(див. рис.34)

7. Визначити величину поперечної сили в перерізі 1-1.

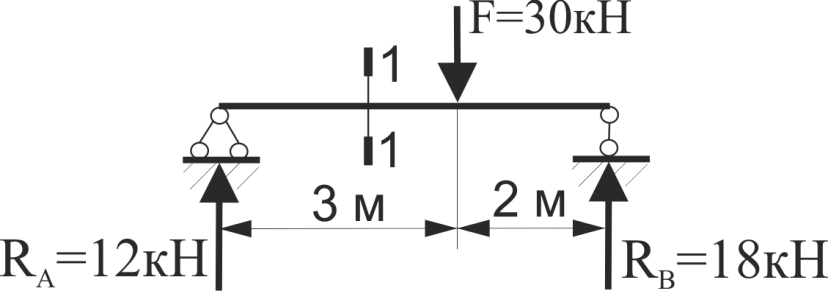
Рис.34.

8. Визначити величину згинального моменту в перерізі 1-1.

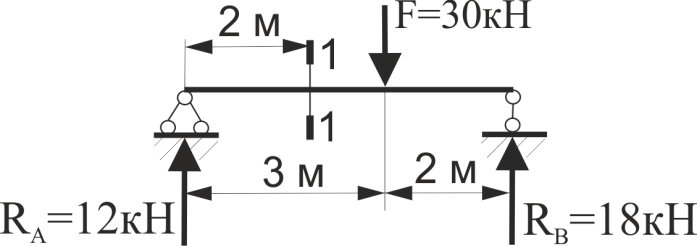
Рис.35.

9. Записати аналітичний вираз згинаючого моменту для перерізу 2-2

Рис.36.

10. Записати аналітичний вираз поперечної сили для перерізу 1-1(див. рис.36)

Обрати правильно побудовані епюри

1. Обрати правильно побудовану епюру поперечних сил для наведеної нижче схеми:

Рис.37

2. Обрати правильно побудовану епюру поперечних сил для наведеної нижче схеми:

Рис.38

3. Обрати правильно побудовану епюру поперечних сил для наведеної нижче схеми

Рис.39

4. Обрати правильно побудовану епюру поперечних сил для наведеної нижче схеми

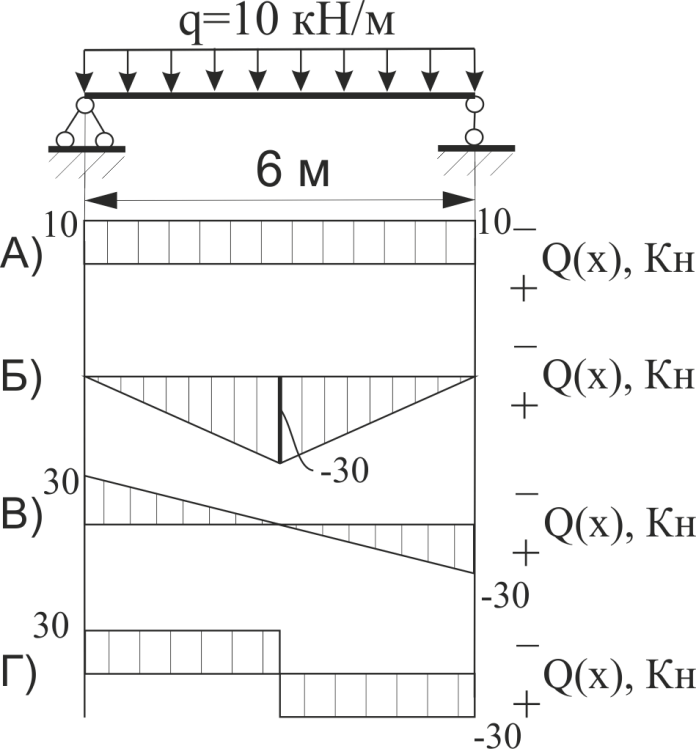
Рис.40

5. Обрати правильно побудовану епюру поперечних сил для наведеної нижче схеми

Рис.41

5. Обрати правильно побудовану епюру згинальних моментів для наведеної нижче схеми

Рис.42

5. Обрати правильно побудовану епюру згинальних моментів для наведеної нижче схеми

Рис.43

5. Обрати правильно побудовану епюру згинальних моментів для наведеної нижче схеми

Рис.44

Визначення нормальних напружень у заданій точці поперечного перерізу

1. Визначити абсолютне значення нормального напруження в точці А, якщо згинаючий момент в цьому перерізі . Відповідь вказати в МПа.

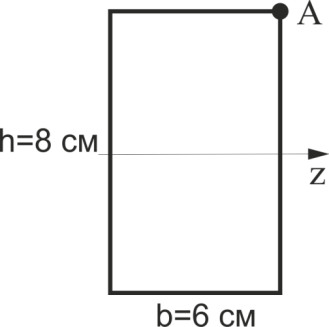
Рис.45

2. Визначити абсолютне значення нормального напруження в точці А, якщо згинаючий момент в цьому перерізі . Відповідь вказати в МПа.

Рис.46

3. Визначити абсолютне значення нормального напруження в точці А, якщо згинаючий момент в цьому перерізі . Відповідь вказати в МПа.

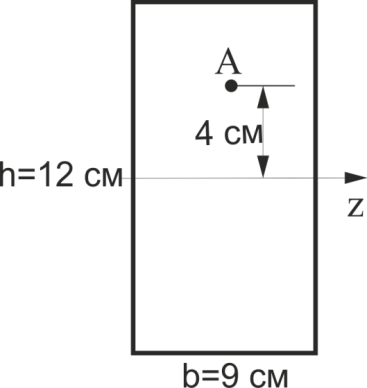
Рис.47

4. . Визначити абсолютне значення нормального напруження в точці А, якщо згинаючий момент в цьому перерізі . Відповідь вказати в МПа.

Рис.48

5. Визначити абсолютне значення нормального напруження в точці А, якщо згинаючий момент в цьому перерізі . Відповідь вказати в МПа.

Рис.49

6. Визначити абсолютне значення нормального напруження в точці А, якщо згинаючий момент в цьому перерізі . Відповідь вказати в МПа.

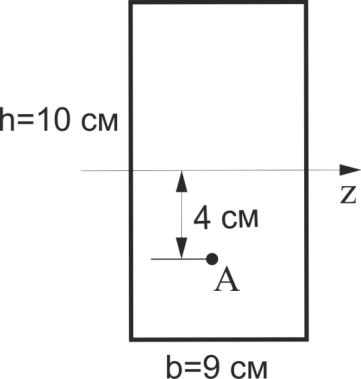
Рис.50

7. Визначити абсолютне значення найбільшого напруження в небезпечному перерізі двотаврової балки. Момент інерції двотавра № 20 дорівнює 2000 см⁴

Рис.51

8. Визначити абсолютне значення найбільшого напруження в небезпечному перерізі двотаврової балки. Момент інерції двотавра № 14 дорівнює 560 см⁴

Рис.52

9. Визначити абсолютне значення найбільшого напруження в небезпечному перерізі двотаврової балки. Момент інерції двотавра № 12 дорівнює 360 см⁴.

Рис.53.

10. Визначити абсолютне значення найбільшого напруження в небезпечному перерізі двотаврової балки. Момент інерції двотавра № 24 дорівнює 3600 см⁴

Рис.54

Добір перерізу балки при згині

1. Виконати добір балки двотаврового перерізу, якщо найбільший згинальний момент дорівнює 16 кНм, а допустиме напруження матеріалу [] = 200 МПа.

а) №10, W_z = 39,7 см³; б) №12, W_z = 58,4 см³;

в) №14, W_z = 81,7 см³; г) №16, W_z = 109 см³.

д)№20, W_z = 184 см³; е) №36, W_z = 743 см³.

2. Виконати добір балки двотаврового перерізу, якщо найбільший згинальний момент дорівнює 11кНм, а допустиме напруження матеріалу [] = 170 МПа.

а) №10, W_z = 39,7 см³; б) №12, W_z = 58,4 см³;

в) №14, W_z = 81,7 см³; г) №16, W_z = 109 см³.

д)№20, W_z = 184 см³; е) №36, W_z = 743 см³.

3. Виконати добір балки двотаврового перерізу, якщо найбільший згинальний момент дорівнює 12кНм, а допустиме напруження матеріалу [] = 140 МПа.

а) №10, Wz = 39,7 см3; б) №12, Wz = 58,4 см3;

в) №14, Wz = 81,7 см3; г) №16, Wz = 109 см3.

д)№20, Wz = 184 см3; е) №36, Wz = 743 см3.

4. Виконати добір балки двотаврового перерізу, якщо найбільший згинальний момент дорівнює 63кНм, а допустиме напруження матеріалу [] = 120 МПа.

а) №10, Wz = 39,7 см3; б) №12, Wz = 58,4 см3;

в) №14, Wz = 81,7 см3; г) №16, Wz = 109 см3.

д)№20, Wz = 184 см3; е) №36, Wz = 743 см3.

5. Виконати добір балки двотаврового перерізу, якщо найбільший згинальний момент дорівнює 24кНм, а допустиме напруження матеріалу [] = 160 МПа.

а) №10, Wz = 39,7 см3; б) №12, Wz = 58,4 см3;

в) №14, Wz = 81,7 см3; г) №16, Wz = 109 см3.

д)№20, Wz = 184 см3; е) №36, Wz = 743 см3.

Розділ III. Деформації при згинанні.

Теоретичні питання.

1. Які припущення приймаються при визначенні переміщень у балках?

2. Записати диференційне рівняння зігнутої осі балки 2-го порядку.

3. З яких умов знаходяться постійні інтегрування диференційного рівняння зігнутої осі балки 2-го ?

4. Записати граничні умови для вказаної балки

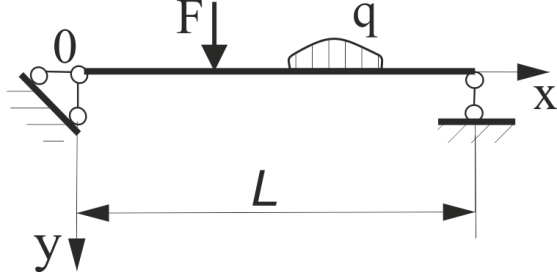
Рис.55.

5. Записати диференційне рівняння зігнутої осі балки 4-го порядку.

6. Скільки постійних з’являються при інтегруванні диференційного рівняння зігнутої осі балки 4-го порядку?

7. Записати універсальне рівняння зігнутої осі балки .

8. Від чого залежить вираз в універсальному рівнянні зігнутої осі балки.

9. Записати диференціальну залежність між кутом повороту та прогином.

10. Оберіть вірні граничні умови для вказаної балки для визначення переміщень методом початкових параметрів.

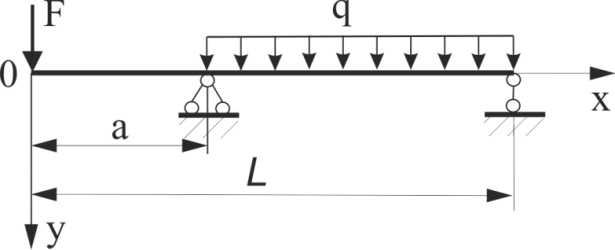
Рис.56.

11. Скільки постійних одержимо при інтегруванні диференційного рівняння зігнутої осі балки 2-го порядку для заданої балки?

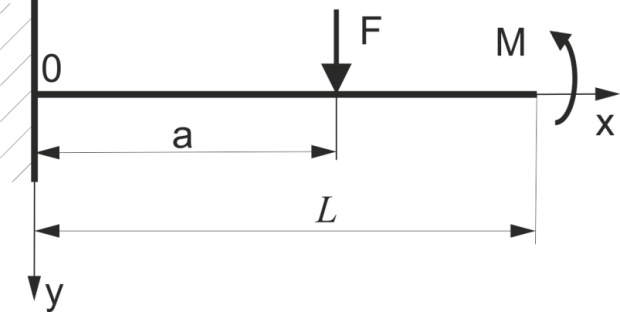
Рис.57.

12. Для вказаної балки записати складову v*(х) універсального рівняння зігнутої осі балки.

Рис.58.

13. Для вказаної балки записати складову v*(х) універсального рівняння зігнутої осі балки.

Рис.59.