
- •1.1 Расчет статически неопределимой стержневой системы при осевом растяжении (сжатии)
- •Расчет статически неопределимой системы при осевом растяжении (сжатии)
- •2.1 Определение внутренних усилий вала. Построение эпюр
- •2.2 Определение внутренних усилий вала. Построение эпюр
- •3.1 Определение опорных реакций статически определимой балки. Построение эпюр
- •3.2 Расчет многопролетной статически определимой балки
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего
профессионального образования
АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
(ФГБОУ ВПО «АмГУ»)
Факультет Энергетический
Кафедра Автоматизации производственных процессов и электротехники
Специальность 160400.65- Проектирование, производство и эксплуатация ракет и ракетно-космических комплексов
КУРСОВАЯ РАБОТА
на тему: Простые виды нагружений. Расчеты на прочность и жесткость
по дисциплине «Сопротивление материалов»
Исполнитель
студент группы 212ос В. А. Мищенко
Руководитель
старший преподаватель М. Е. Бошко
Нормоконтроль
зав. лабораторией Н. Н. Гужикова
Благовещенск 2014
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего
профессионального образования
АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
(ФГБОУ ВПО «АмГУ»)
Факультет Энергетический
Кафедра Автоматизации производственных процессов и электротехники
ЗАДАНИЕ
К курсовой работе студента 212-ос группы Мищенко Виолетты Александровны.
1. Тема курсовой работы: Простые виды нагружений. Расчеты на прочность и жесткость.
2. Срок сдачи студентом законченной работы: до 07.06.2014 г.
3. Исходные данные к курсовой работе: указаны, непосредственно, в условиях задач.
4. Содержание курсовой работы:
- осевое растяжение (сжатие): расчет статически определимых и неопределимых стержней;
- кручение: расчет статически неопределимого вала, расчет ступенчатого вала;
- прямой и поперечный изгиб: расчет статически определимых балок;
- расчет статически определимой рамы.
5. Дата выдачи задания 11.02.2014 г. Руководитель курсовой работы: Бошко Маргарита Евгеньевна, старший преподаватель.
Задание принял к исполнению 11.02.2014 г.:______________
РЕФЕРАТ
Курсовая работа содержит 48 с., 38 рисунков, 5 источников.
МОМЕНТ ИНЕРЦИИ, НОРМАЛЬНОЕ НАПРЯЖЕНИЕ, КАСАТЕЛЬНОЕ НАПРЯЖЕНИЕ, СИЛА, КРУТЯЩИЙ МОМЕНТ, ШВЕЛЛЕР, ЖЕСТКАЯ ЗАДЕЛКА, БАЛКА, ДВУТАВР, РАДИУС ИНЕРЦИИ, ОТНОСИТЕЛЬНОЕ ПЕРЕМЕЩЕНИЕ, ЗАКОН ГУКА, УГОЛ ПОВОРОТА, РАМА
Курсовая работа посвящена решению различных типов задач и построению к ним эпюр:
Осевое растяжение (сжатие);
Кручение;
Изгиб.
СОДЕРЖАНИЕ
Введение 5
Осевое растяжение (сжатие) 6
Расчет статически неопределимой стержневой системы при осевом растяжении (сжатии) 6
Расчет статически неопределимой системы при осевом растяжении (сжатии) 10
Кручение 14
Определение внутренних усилий вала. Построение эпюр 14
Определение внутренних усилий вала. Построение эпюр 18
Изгиб 23
Определение опорных реакций статически определимой балки. Построение эпюр 23
Расчет многопролетной статически определимой балки 35
Расчет плоских статически определимых рам 42
Заключение 47
Библиографический список 48
Введение
Основной целью изучения курса "Сопротивление материалов" является усвоение будущим инженером основных подходов и методов проведения расчетной оценки конструкций, работающих при разнообразных видах нагружения на прочность и жесткость.
Методами сопротивления материалов выполняются расчеты, на основании которых определяются необходимые размеры деталей машин и конструкций инженерных сооружений. Любая конструкция должна обладать надежностью при эксплуатации и быть экономичной.
Надежность конструкции обеспечивается, если она сохраняет прочность, жесткость и устойчивость при гарантированной долговечности. Ее экономичность в значительной мере определяется расходом материала, применением менее дефицитных конструкционных материалов, возможностью изготовления деталей по наиболее прогрессивным технологиям.
ОСЕВОЕ РАСТЯЖЕНИЕ (СЖАТИЕ)
1.1 Расчет статически неопределимой стержневой системы при осевом растяжении (сжатии)
Постановка задачи:
Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням с помощью шарниров.
Требуется:
Найти усилия и напряжения в стержне, выразив их через силу Q;
Найти допускаемую нагрузку Q, приравняв большее из напряжений в двух стержнях допускаемому напряжению
 ;
;Найти предельную грузоподъемность при
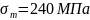 ;
;Определить перемещение точки приложения силы Q.
Дано:
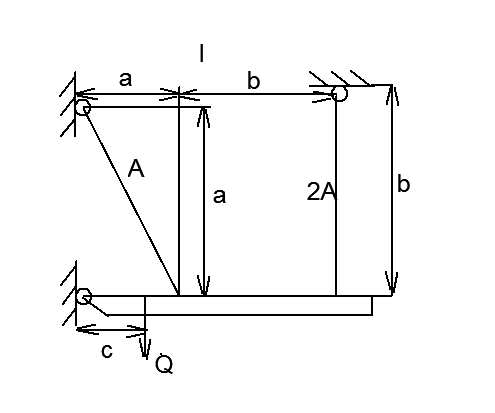
Рисунок 1 – Схема статически неопределимой системы
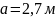 ,
,
 ,
,
 ,
, ,
,
.
,
,
.
Данная
система статически неопределима 1 раз,
поскольку имеем 4 неизвестных -
 .
.
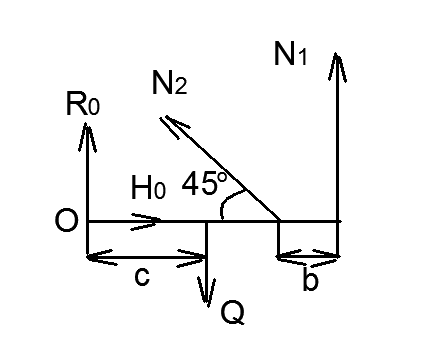
Рисунок 2 – Схема внутренних усилий системы
Уравнение равновесия:
 ;
(1)
;
(1)
 ;
(2)
;
(2)
 .
(3)
.
(3)
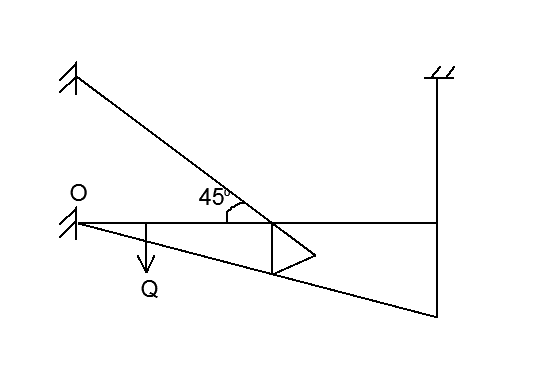
Рисунок 3 – Схема деформации системы
Перемещение
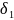 концевого сечения первого стержня
совпадает с его продольной деформацией
Δ
концевого сечения первого стержня
совпадает с его продольной деформацией
Δ (
( .
Второй стержень, чтобы совместить
начальное положение его концевого
сечения с конечным, надо растянуть его
.
Второй стержень, чтобы совместить
начальное положение его концевого
сечения с конечным, надо растянуть его
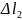 и повернуть вдоль касательной по часовой
стрелке.
и повернуть вдоль касательной по часовой
стрелке.
Касательная
будет перпендикулярна продольной оси
второго стержня. При этом Δ
 (треугольник деформации второго стержня).
(треугольник деформации второго стержня).
 – перемещение точки прикрепления
стержней 1 и 2 к жесткому брусу, а Δ
,
Δ
– перемещение точки прикрепления
стержней 1 и 2 к жесткому брусу, а Δ
,
Δ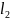 – продольные деформации стержней 1 и
2.
– продольные деформации стержней 1 и
2.
Закон Гука для осевого растяжения (сжатия):
Δ .
(4)
.
(4)
Cоставляем уравнение деформации из подобия треугольников деформации:
 ;
(5)
;
(5)
 ;
(6)
;
(6)
 ;
(7)
;
(7)
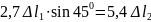 ;
(8)
;
(8)
 ;
(9)
;
(9)
 .
(10)
.
(10)
Решаем уравнение деформации и статики совместно:
 ;
(11)
;
(11)
 .
(12)
.
(12)
Получаем:
 ;
(13)
;
(13)
 .
(14)
.
(14)
Усилия в стержне, выраженные через силу Q:
 ;
(15)
;
(15)
 .
(16)
.
(16)
Найдем напряжения в стержне, выразив их через силу Q:
 ;
(17)
;
(17)
 ;
(18)
;
(18)
 (опасное
сечение).
(19)
(опасное
сечение).
(19)
Допускаемую нагрузку находим из условия прочности по нормальным напряжениям, если :
 ;
(20)
;
(20)
 ;
(21)
;
(21)
 кН.
(22)
кН.
(22)
Найдем предельную грузоподъемность при . Для ответа на этот вопрос следует иметь ввиду, что в одном из стержней напряжение, как правило, больше, чем в другом.
При
повышении нагрузки напряжение в наиболее
напряженном стержне достигает предела
текучести раньше, чем во втором. Затем,
при дальнейшем повышении нагрузки
(напряжение в первом стержне на некотором
этапе нагружения расти не будет и усилие
 (предельное)) достигается предел текучести
и во втором стержне
(предельное)) достигается предел текучести
и во втором стержне
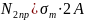 .
.
Подставив
в уравнение статики предельные значения
усилий в стержнях, найдем из него
предельную грузоподъемность
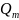 :
:
 ;
(23)
;
(23)
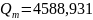 кН.
(24)
кН.
(24)
Вывод: предельная грузоподъемность стержня больше допускаемой нагрузки.
 .
(25)
.
(25)
Находим перемещение точки приложения силы Q:
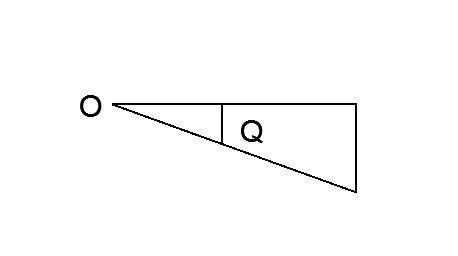
Рисунок 4 – Схема перемещения точки приложения силы Q
 ;
(26)
;
(26)
 м.
(27)
м.
(27)
