2.2. Расчет действительного профиля кулачка.

2.2.1 Расчет действительного профиля кулачка на фазе удаления.

1. Угол поворота кулачка.

φ₄=51⁰=0,89 (рад)

2. Значение функции перемещения:

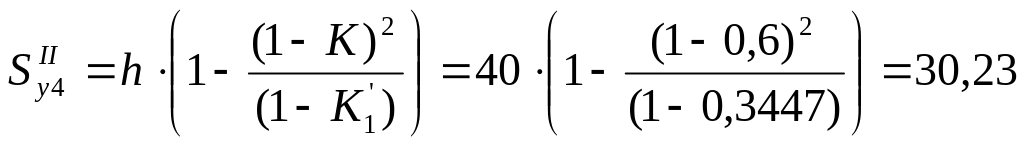(мм)

3. Значение функции аналога скорости

(мм)

4. Значение угла давления

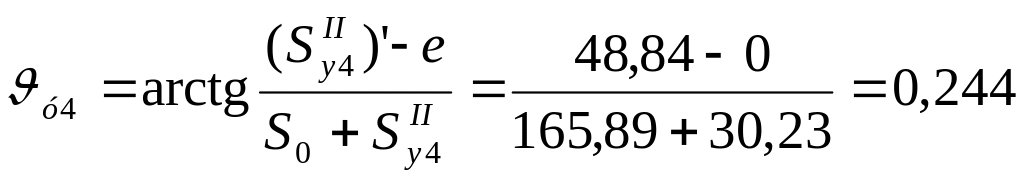(рад)

5. Полярный угол для радиус-вектора теоретического профиля.

6. Длина радиус-вектора теоретического профиля:

(мм)

7. Длина радиус-вектора действительного профиля:

(рад)

(мм)

8. Полярный угол для радиус-вектора R₄ действительного профиля:

(рад)

=20,87⁰

2.2.2 Расчет действительного профиля кулачка на фазе возвращения.

1. Угол поворота кулачка.

φ₁₀=146⁰=2,548 (рад)

2. Значение функции перемещения:

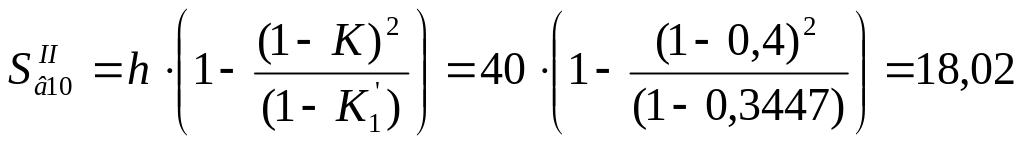(мм)

3. Значение функции аналога скорости

(мм)

3. Значение угла давления

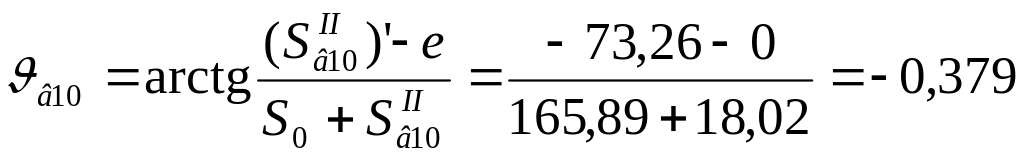(рад)

3. Полярный угол для радиус-вектора теоретического профиля.

3. Длина радиус-вектора теоретического профиля:

(мм)

3. Длина радиус-вектора действительного профиля:

(рад)

(мм)

3. Полярный угол для радиус-вектора R₄ действительного профиля:

(рад)

=-32,99⁰

Глава 3. Анализ плоских рычажных механизмов

3.1.Определение размеров звеньев

1. Угол качания кулисы:

2. Длина кулисы:

S=H

(м)

3. Длина кривошипа:

OA=r

(м)

4. Длина шатуна:

(м)

5. Угол поворота кривошипа на холостом ходу рабочего звена:

6. Угол поворота кривошипа на рабочем ходу выходного звена

3.2. Построение плана скоростей

3.2.1 Построение плана скоростей для диады впв

1. Определение скорости точки А:

1.1 Угловая скорость кривошипа:

(рад/с)

1.2 Скорость точки А:

(м/с)

2. Составление системы векторных уравнений:

В точке А в каждый момент времени находятся точки А₁ А₂ А₃ принадлежащие звеньям 1, 2 и3

2. Масштабный коэффициент для построения плана скоростей:

2. Определяем скорости A₃

(м/с)

(м/с)

2. Скорость точки D определим используя правило подобия:

(м/с)

(мм)

2. Скорость точки S₃ определим используя правило подобия:

(м/с)

(м/с)

2. Угловая скорость кулисы:

(рад/с)

3.2.2. Построение плана скоростей для диады ввп

1. Для точки Е составим 2-а векторных уравнения, рассмотрев движение этой точки относительно точки D и относительно оси ОХ.

=0

(м/с)

(м/с)

2. Скорость точки S₃ определим используя правило подобия: т.к. S₄ середина DE, то на плане скоростей находим середину DE.

(м/с)

3. Угловая скорость шатуна

(рад/с)

3.3. Построение плана ускорений

3.3.1 Построение плана ускорений для диады впв

1. Определение нормального ускорения кривошипа:

( )

2. Масштабный коэффициент для построения плана ускорений:

3. Составим систему векторных уравнений ускорения точки A₃

4. Определение величины и направления кориолисова ускорения:

(

Направление кориолисова ускорения определяем поворотом скорости на 90⁰ в сторону угловой скорости ω₃

4. Длина вектора кориолисова ускорения:

= (мм)

5. Определение величины нормального ускорения кулисы и длины вектора нормального ускорения кулисы

(

(мм)

6. Определяем неизвестные величины из плана ускорений:

(

(

(

7. Ускорения точек D и S₃ найдем используя правило подобия:

(

Pd= (мм)

(

(мм)

8. Определяем угловое ускорение

(

Кулиса движется ускоренно.