Решение дифференциальных уравнений в среде Maple Примеры решения уравнений встроенными функциями

1. Решить дифференциальное уравнение .

Примечание 1. Производная в Maple задаётся функцией diff.

Синтаксис:

diff(<от чего производная>,<по какой переменной>)

diff(y(x),x) – первая производная по x от функции y, зависящей от x;

diff(y(x),x$n) – n-ая производная по x от функции y, зависящей от x.

Например:

> diff(sin(x),x);

> diff(sin(x),x$3);

Diff – инертная форма функции производной.

Например:

> Diff(tan(x),x)=diff(tan(x),x);

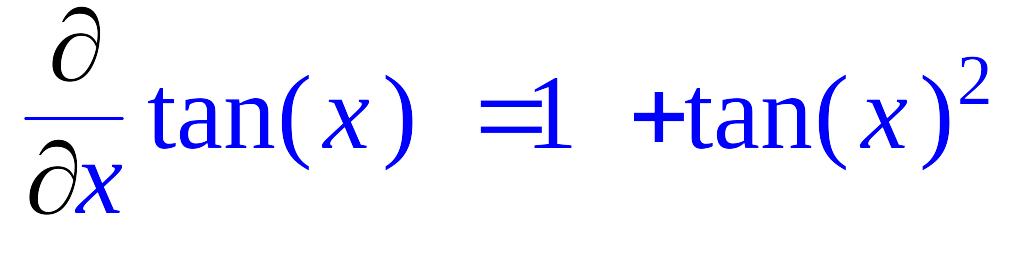
Для решения обыкновенных дифференциальных уравнений (ОДУ) и систем ОДУ, зависящих от одной переменной, используется функция dsolve.

Синтаксис:

dsolve(<уравнение или система>,<по какой функции или функциям получить решение>)

dsolve({<уравнение или система>[,<условие1>,<условие2>,…]},<по какой функции или функциям получить решение>)

Решение:

> dsolve(diff(y(x),x$2)-4*diff(y(x),x)+13*y(x)=0,y(x));

2. Решить задачу Коши , если: .

Примечание 2. В обозначении граничных условий с производными используется дифференциальный оператор D (используется только с большой буквы) D(f)(0) – обозначает значение производной от функции f в нуле. Например, если f зависит от x, то это будет обозначать следующее: .

В функции dsolve уравнение и граничные условия записываются в виде списка или множества (описание см. Синтаксис среды Maple).

Решение.

>dsolve([diff(y(x),x$2)+2*diff(y(x),x)+5*y(x),y(0)=2,D(y)(0)=6],y(x));

3. Решить систему ОДУ

Примечание 3.

Все уравнения системы и условия записываются в общем одномерном списке или множестве. Набор функций, по которым производится интегрирование системы, также записывается в виде списка или множества.

Для начала необходимо выбрать переменную, от которой зависят x и у. Она не должна иметь имя уже объявленного оператора, константы, функции или переменной, иначе это приведет к ошибке. Каким образом отменить определение пользовательской переменной описано выше (см. Синтаксис среды Maple). В нашем случае переменная t.

Решение.

>dsolve({diff(x(t),t)=2*x(t)+3*y(t),diff(y(t),t)=5*x(t)+4*y(t)},{x(t),y(t)});

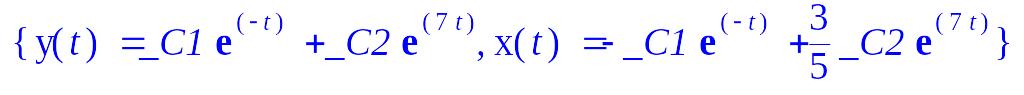
4. Решить систему ОДУ , при , .

Решение.

>dsolve({diff(x(t),t)=2*x(t)+3*y(t),diff(y(t),t)=5*x(t)+4*y(t),x(0)=15,D(y)(0)=20},{x(t),y(t)});

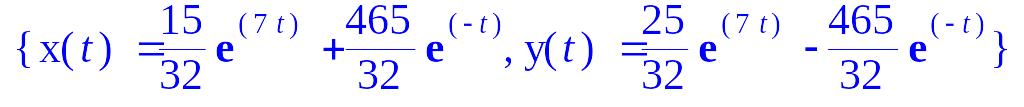
Примечание 4. Для получения конечного результата с действительными числами используется функция evalf.

Синтаксис:

evalf(<выражение>)

evalf[n](<выражение>) или evalf(<выражение>,n)

В первом примере функция evalf преобразует все выражения к виду с действительными числами с количеством значащих цифр, определяемым в системной переменной Digits. Во втором случае используется количество цифр, определенное пользователем (n).

Изменить системную переменную Digits можно обычным присваиванием ей целочисленного значения. В результате все операции с плавающей точкой будут использовать именно такое количество значащих цифр.

Для рассматриваемого примера:

>evalf(%);

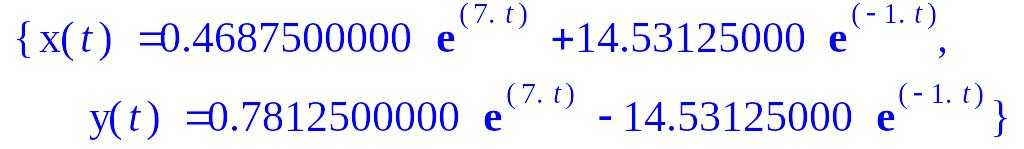
Дифференциальные уравнения можно записывать и с помощью оператора D. Для перехода между формами записи дифференциальных уравнений используется функция convert с параметром D или diff. Рассмотрим пример программы с использованием различных форм записи.

> restart;

> a1:=diff(y(x),x$2)+13*diff(y(x),x)+10=0;

convert(%, D);

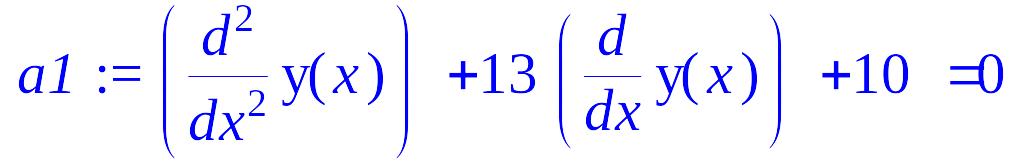
> a2:=(D@@2)(y)(x)+13*D(y)(x)+10;

convert(%, diff);

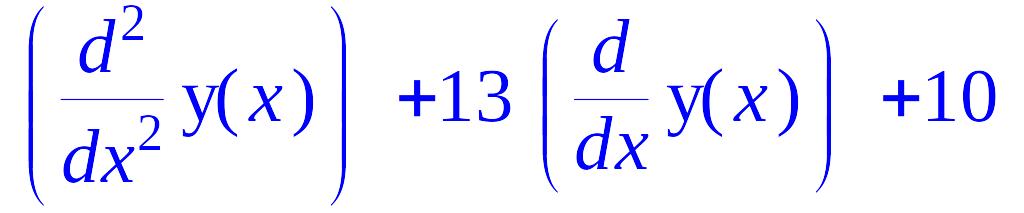
> dsolve(a2,y(x));

dsolve(a1,y(x));

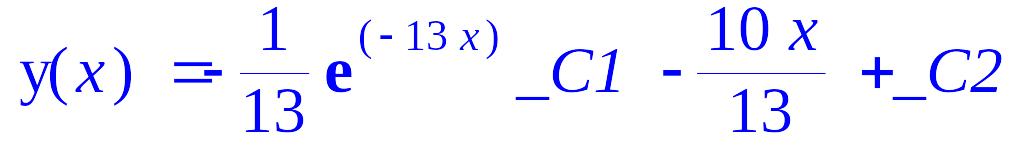
Сначала производим отмену всех определений. Затем переменной а1 присваиваем значение дифференциального уравнения с использованием diff и преобразуем его к виду с использованием оператора D. После этого для сравнения переменной a2 присваиваем значение дифференциального уравнения записанного с использованием оператора D и преобразуем к виду с diff. Затем решаем поочередно оба уравнения. Результаты совпадают, следовательно, обе формы записи аналогичны.

Выражение с помощью diff можно записать так: diff(y(x),x$n). Здесь используется оператор перечисления $. Это выражение аналогично записи, где переменная x записана через запятую n раз. Аналогия с помощью оператора D выглядит следующим образом: (D@@n)(y)(x). В данном случае применяется оператор вложенности @@, т. е. сначала берется производная, а затем от нее еще производная и так n раз.