Лабораторная работа №2 Решение системы нелинейных уравнений
Задача. Данную систему нелинейных уравнений решить несколькими методами. 1) методом итераций; 2) методом Ньютона; 3) с помощью функций MathCAD. Результаты сравнить. Каждый пункт задания выполнять в отдельном документе. Точность решения принять равной 10-3.
Решение. 1.
Задаются уравнения. C
клавиатуры вводится имя переменной, в
которую заносится уравнение, вводится
левая часть, ставится знак равенства
клавишей
на панели Boolean,
вводится правая часть. Греческие буквы
вводятся с помощью панели Greek.
Возведение в степень осуществляется с
помощью знака “^” (10^-3) или клавиши
на панели Calculator.
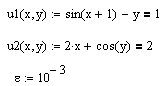
Теперь выражаются
искомые переменные. Их надо выразить
обе, по одной из каждого уравнения.
Получатся две функции, каждая из которых
будет зависеть только от одной переменной.
С клавиатуры
вводится имя функции, ставится знак
присваивания, на панели Symbolic
нажимается клавиша
,
слева от появившейся функции «■
solve,
■» пишется
имя уравнения, справа – выражаемая
переменная. Нажимается ввод.
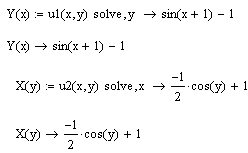
Далее графическим
способом определяются начальные
приближения. Для
построения графика на панели Graph
нажимается клавиша
,
появляется шаблон графика. Для
горизонтальной оси (под графиком)
вводится «x,X(y)»,
для вертикальной оси (слева от графика)
– «Y(x),y».
При вводе этих значений появятся поля
для ввода предельных значений абсциссы
и ординаты, которые можно не указывать
(по умолчанию – от -10 до 10), но потом их
можно будет изменить. Нажимается «Enter».
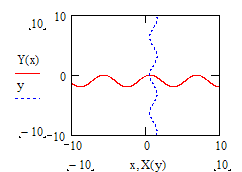
Для более точного
определения координаты точки пересечения
графиков требуется: а) щелкнуть по
графику левой клавишей мышки (войти в
график); б) на панели Graph
нажать клавишу
,
откроется окно X-Y
Zoom;
в) расположить это окно так, чтобы
оно не закрывало рисунок; г) держа нажатой
левую клавишу мыши, выделить на графике
область пересечения графиков (в полях
окна X-Y
Zoom
отобразятся координаты выделенной
области); д) нажать последовательно
клавиши
и
в окне X-Y
Zoom;
е) теперь, когда область пересечения
графиков функций увеличена, необходимо
войти в график и нажать клавишу
на панели
Graph;
ж) Открывшееся окно X-Y
Trace
расположить так, чтобы оно не закрывало
рисунок; з) левой клавишей мыши щелкнуть
в месте пересечения графиков. В полях
окна X-Y
Trace
появятся значения координат в месте
щелчка. Эти координаты следует взять в
качестве начального приближения .Окно
X-Y
Trace
можно закрыть.
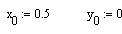
Далее организовывается итерационный цикл.
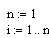
Такие циклы MathCAD обрабатывает только в числовом виде, поэтому , искомым переменным необходимо сначала присвоить числовые значения, например нулевые, затем просчитать значения итерационные.
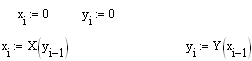
После этого цикла
оценивается погрешность и выводятся
все найденные значения. Знак
квадратного корня ставится нажатием
клавиши
на панели Calculator.
Возведение в квадрат можно поставить
нажатием клавиши
на той же панели.
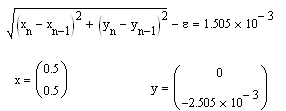
Если выведенная разность отрицательна, то точность достигнута, если она положительна, то необходимо вернуться к началу цикла (n:=..) и увеличить значение n на единицу (Например, вместо n:=1 написать n:=2). И так до тех пор, пока не будет достигнута точность.
2. Для решения методом Ньютона создается новый документ, а в уравнениях системы все слагаемые переносятся в одну сторону и уравнения системы задаются как функции двух переменных.
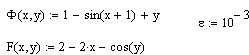
Задаются еще две
функции и начальные приближения.
Числитель и
знаменатель каждой дроби ставится так:
вводится знак определителя нажатием
клавиши
на панели Matrix,
внутри него ставится матрица 2х2. Оператор
дифференцирования вводится нажатием
клавиши
на панели Calculus.
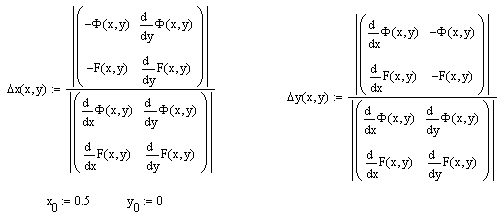
Как и в первом методе организуется итерационный цикл, оценивается погрешность и выводятся найденные значения. Если точность не будет достигнута, то в начале цикла n увеличивается на 1.
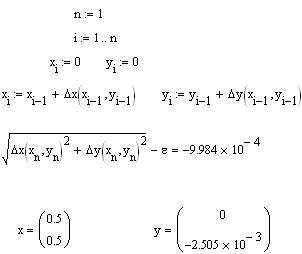
3. И наконец, система уравнений решается с помощью функций MathCAD. В новом документе задаются начальные приближения;
Пишется ключевое
слово
и ниже него система уравнений;
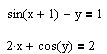
После этого решение находится с помощью функции Find:
.
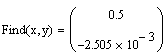