Метод Якоби

Чтобы решить систему

(5.10)

методом простой итерации, необходимо привести ее к виду

. (5.11)

После того, как мы выяснили, каким условиям должна удовлетворять матрица для сходимости метода, следует выяснить как привести систему (5.10) к виду (5.11), чтобы это условие сходимости выполнялось.

Представим матрицу системы (5.10) в виде:

,

где – диагональная, и – левая и правая строго треугольные (т.е. с нулевой диагональю) матрицы. Тогда система (5.10) может быть записана в виде:

.

Если на диагонали исходной матрицы нет нулей, то эквивалентной (5.10) задачей вида (5.11) будет

, (5.12)

т. е.

, .

Метод простых итераций, основанный на таком приведении системы (5.10) к виду (5.11), называется метод Якоби . Тогда последовательность приближений по методу простой итерации имеет вид:

.

Здесь – обратная к матрице – диагональная матрица

, ,

поэтому представление системы в виде (5.12) равнозначно выражению диагональных неизвестных:

;

;

.

Теперь для записи итерационного процесса в развернутом виде следует расставить номера итераций:

;

; (5.13)

.

Достаточный признак сходимости метода Якоби к решению системы (5.10) сформулирован в следующей теореме.

Теорема. В случае диагонального преобладания в матрице системы (5.10) метод Якоби (5.13) сходится.

Диагональное преобладание означает, что: .

Тогда в матрице

,

сумма модулей элементов в любой строке меньше единицы , следовательно, одна из норм (по крайне мере одна) матрицы меньше единицы, т. е. метод Якоби сходится.

Метод Зейделя

Под методом Зейделя понимают такое видоизменение метода простых итераций (5.12) решения систем линейных уравнений, приведенных к виду (5.11), при котором при подсчете i-ой компоненты приближения к искомому используются уже найденные на этом шаге новые значения первых компонент, т. е. приближения к решению системы (5.11) по методу Зейделя определяются выражениями:

.

Здесь , - компоненты начального приближения . Эти формулы можно записать в виде:

; .

Если приведение СЛАУ (1) к виду (5.11) основано на представлении (5.12), то метод Зейделя есть модифицированный метод Якоби:

.

Для метода Зейделя

Теорема. Если , то при любом метод Зейделя сходится к точному решению системы и справедливы оценки погрешности:

.

Если матрица имеет диагональное преобладание, то метод Зейделя сходится быстрее, чем метод Якоби.

Пример. Решить систему методом итерации:

Приведем систему к нормальному виду:

Здесь . Вычислим норму матрицы

, следовательно, метод простых итераций сходится.

Пусть , ;

; ; – оценка числа итераций.

Практикум по вычислительной математике Лабораторные работы для Mathcad 2001i Professional Лабораторная работа № 1 Обращение матриц

Задача. 1. Данную квадратную матрицу A разбить на произведение двух треугольных матриц T1 и T2. 2. Для каждой из полученных матриц (T1 и T2) найти обращенную (T1^-1 и T2^-1 соответственно), т.е. такую, чтобы произведение исходной матрицы и обращенной давало единичную (например, T1*T1^-1=E). Произведение обращенных матриц должно давать обращенную матрицу A (T2^-1*T1^-1=A^-1). т.е. необходимо посчитать A^-1, перемножив T1^-1 и T2^-1, и посчитать A^-1 с помощью функций MathCAD. Результаты сравнить.

Решение. 1. Задается исходная матрица A и треугольные матрицы T1 и T2, т.к. в матрицах T1 и T2 коэффициенты неизвестны, то необходимо указать, что эти матрицы зависят от коэффициентов. C клавиатуры вводится имя матрицы, знак присваивания вводится нажатием клавиши на панели Evaluation или клавишей “:”, матрица вводится нажатием клавиши на панели Matrix. Количество строк и столбцов задается равным 4. Ввод нижнего индекса осуществляется с помощью клавиатуры следующим образом: нажимается клавиша “[”, вводится индекс, заканчивается ввод нажатием клавиши “→”. (Нумерация элементов матриц и векторов в MathCAD начинается с нуля).

Теперь выражаются формулы для расчета элементов треугольных матриц. Для этого необходимо посчитать произведение T1 и T2 в символьном (аналитическом) виде. Ниже введенных матриц выводится это произведение. С клавиатуры вводится выражение T1(b)*T2(b), вводится оператор символьного вывода нажатием клавиши на панели Symbolic, нажимается “Enter”.

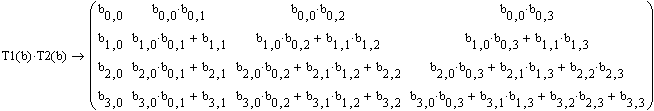
Далее из уравнения T1(b)*T2(b)=A каждый элемент полученного символьного произведения матриц должен быть равен соответствующему элементу матрицы A. Например, для нулевого столбца необходимо реализовать цикл i от 0 до 3, и всем присвоить b_i,0=a_i,0. Это действие выполняется в столбик. С клавиатуры вводится имя циклически изменяемой переменной, знак присваивания, пределы изменения нажатием клавиши на панели Matrix. Ниже операция присваивания. Для проверки можно вывести значения найденных величин. Знак численного вывода вводится клавишей на панели Evaluation.

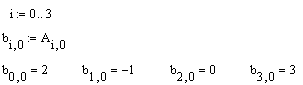
Аналогичным образом вычислить самостоятельно значения остальных коэффициентов для:

j от 1 до 3 b_0,j:=A_0,j/b_0,0 в нулевой строке;

i от 1 до 3 b_i,1:= A_i,1-b_i,0*b_0,1 в первом столбце;

j от 2 до 3 b_1,j:= (A_1,j-b_1,0*b_0,j)/ b_1,1 в первой строке;

i от 2 до 3 b_i,2:= A_i,2-b_i,0*b_0,2-b_i,1*b_1,2 во втором столбце;

b_2,3:= (A_2,3-b_2,0*b_0,3-b_2,1*b_1,3)/ b_2,2 ; b_3,3:= A_3,3- b_3,k*b_k,3.

Скобки можно ввести c клавиатуры или клавишей на панели Calculator. Операция суммирования вводится клавишей на палении Calculus. Теперь производится вывод треугольных матриц и проверка правильности нахождения их элементов.

Если произведение получилось равным исходной матрице A, то элементы найдены верно.

2. Обращение матрицы T1. Вводится новая матрица TT1.

.

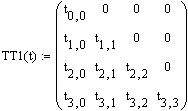Производится символьное умножение.

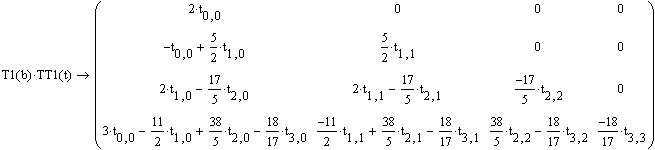
Вычисляются коэффициенты обращенной матрицы сначала на главной диагонали затем вниз от нее:

1) для i от 0 до 3 t_i,i=1/b_i,I ;

2) для i от 1 до 3 t_i,i-1=-t_i-1,i-1*b_i,i-1/b_i,I ;

3) для i от 2 до 3 t_i,i-2=-(t_i-2,i-2*b_i,i-2+t_i-1,i-2*b_i,i-1)/b_i,I ;

4) t_3,0= -( b _3,k*t _k,0)/b_3,3 .

Проверка правильности вычислений.

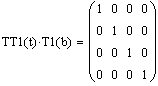
Матрицу T2 обратить самостоятельно. Обращенную матрицу представить в виде

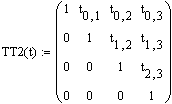
Если символьно перемножить T2 и TT2, получится матрица вида (при выполнении работы не выводить):

.

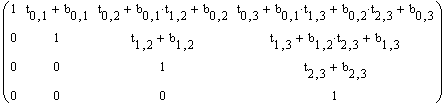Из условия, что все ее элементы, лежащие выше главной диагонали, должны быть равны нулю, и, зная все коэффициенты b_i,j, вывести формулы для нахождения неизвестных коэффициентов t_ij. Использовать циклы и знак суммирования.

Для обращения матрицы с помощью MathCAD на свободном месте документа вводится имя матрицы, знак обращения клавишей на панели Matrix, и знак численного вывода.