Итерационные методы

Итерационные методы решения систем линейных алгебраических уравнений предпочтительнее прямых в случае систем большой размерности.

Рассмотрим метод простой итерации. Пусть требуется решить систему

. (5.6)

Прежде чем применять метод итерации систему (5.6) следует привести к равносильной системе вида

. (5.7)

Здесь – некоторые новые матрицы. Итерационный процесс состоит в том, что последовательно исправляются значения неизвестных. Решение системы получается как предел некоторой единым образом построенной последовательности приближений.

Пусть нам известно некоторое начальное приближение ( о его выборе скажем позже). Подставим в правую часть равенства (5.7), получим следующее приближение:

,

затем поступим с аналогично, получим и так далее:

;

. (5.8)

Таким образом строится последовательность матриц -столбцов .

Если последовательность матриц-столбцов сходится к решению системы , то говорят, что метод итерации для данной системы сходится.

Можно доказать, что если последовательность имеет предел , то этот предел является решением системы (5.7), а следовательно, и (5.6). Если формально в равенстве (5.8) перейти к пределу при , то т. к. , то равенство (5.8) примет вид , т. е. предел является решением системы (5.7). Выясним условия, при которых последовательность имеет предел.

Рассмотрим последовательность решений системы (5.7)

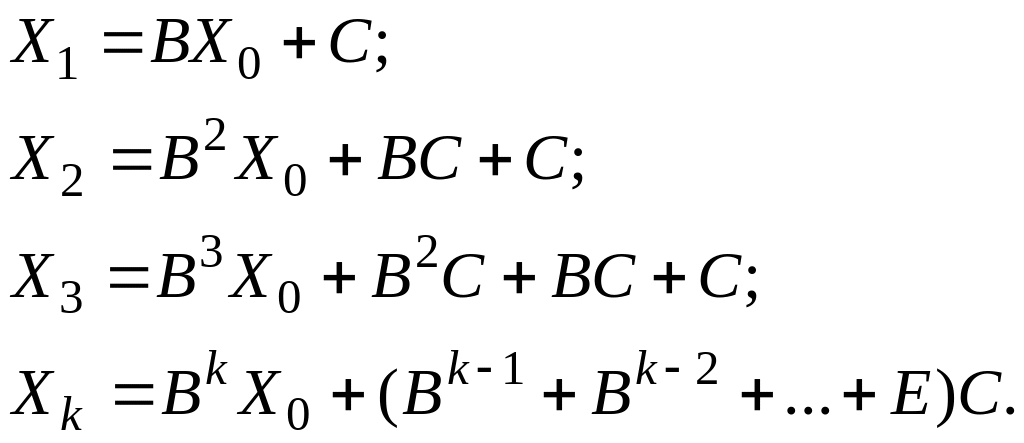
Получается в скобках сумма конечного числа матриц:

,

при получим матричный ряд

. (5.9)

Лемма. Для того, чтобы необходимо и достаточно, чтобы все собственные числа матрицы были бы по модулю меньше единицы: .

Допустим, что все собственные числа матрицы различны, тогда существует невырожденная матрица , такая, что , где – диагональная матрица

,

тогда матрица может быть преобразована к диагональному виду:

.

Возведем в степень обе части по правилам действия с матрицами

;

.

Здесь

.

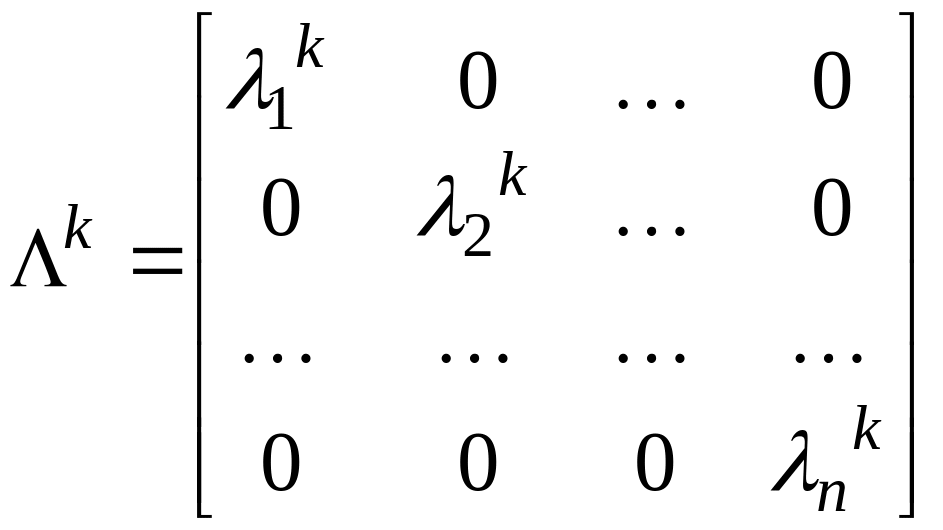Для того, чтобы , необходимо и достаточно, чтобы , а для этого необходимо и достаточно, чтобы .

На практике легче вычислить норму матрицы, чем решать задачу о нахождении собственных значений, поэтому удобнее использовать следующую теорему, дающую достаточные условия.

Теорема. Для того, чтобы , достаточно, чтобы какая-нибудь из норм матрицы была меньше единицы.

На основании свойств нормы можно записать . Т. к. , это и означает, что .

Верно утверждение о том, что модуль каждого собственного числа матрицы не превосходит любой из ее норм .

Теорема. Для того, чтобы ряд сходился, необходимо и достаточно, чтобы , при этом сумма ряда равна .

Необходимость условия очевидна. Докажем достаточность. Пусть , следовательно, , значит, нет ни одного собственного числа, равного единице, тогда и существует обратная матрица . Обозначим сумму сходящегося ряда

.

Рассмотрим выражение:

тогда

, .

Теорема. Необходимое и достаточное условие сходимости метода итераций. Для того, чтобы метод простых итераций сходился при любом начальном векторе , необходимо и достаточно, чтобы все собственные значения матрицы были бы по модулю меньше единицы.

Необходимость. Пусть , тогда является решением системы (5.7), следовательно,

, .

Вычтем из первого равенства второе, получим:

.

К разности можно применить аналогичные рассуждения:

,

т. к. , то , поскольку – произвольный вектор, то , , следовательно, все собственные числа матрицы по модулю меньше единицы.

Достаточность. Пусть . Перейдем в равенстве

к пределу при , тогда , , следовательно , а это решение системы (5.7), а значит и системы (5.6).

Проверить выполнение условий доказанной теоремы довольно трудно. Для практического применения метода итераций нужно иметь достаточные условия , которые даются в следующей теореме.

Теорема. Для того, чтобы метод простых итераций сходился при любом начальном векторе к единственному решению , достаточно, чтобы какая-нибудь норма матрицы была меньше единицы , при этом справедливы оценки погрешности:

– апостериорная;

– априорная.

Априорная оценка, как правило, грубее апостериорной.

Априорная оценка позволяет подсчитать заранее число итераций, достаточное для получения с заданной точностью при выбранном начальном векторе . Для этого нужно найти наименьшее целое решение неравенства

относительно : , т. к. , .

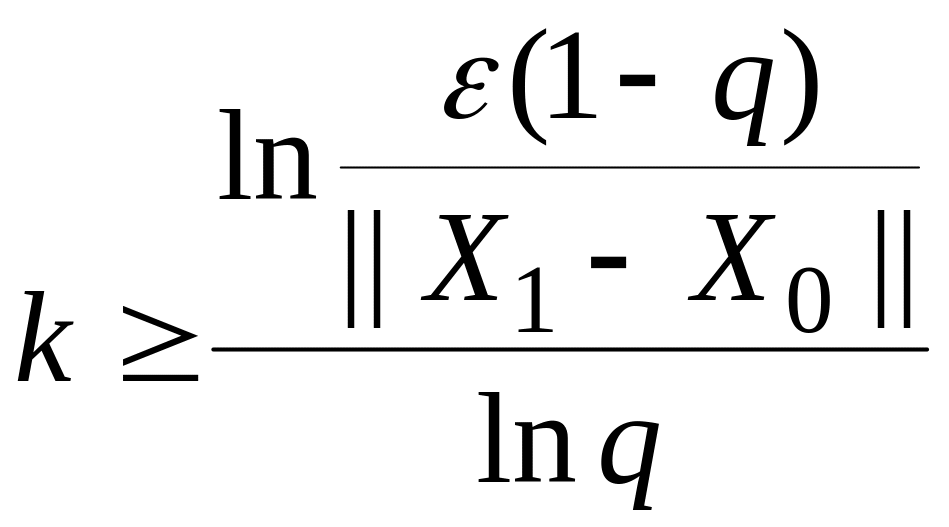Апостериорной оценкой удобно пользоваться непосредственно в процессе вычислений и останавливать этот процесс, как только выполнится неравенство .

Отметим, что неравенство будет гарантией того, что только, если .

Обычно за принимают вектор – матрицу-столбец свободных членов системы (5.7), если неизвестно какое-нибудь близкое решение. Если , то априорная оценка имеет вид:

– при любом .

Дополнительно отметим, что процесс итераций сходится, если все элементы , где – число неизвестных.