Пример 8

Рассмотрим следующие работы и времена их выполнения на соответствующих машинах.

Работа	Продолжительность, ч
	Машина 1, t1	Машина 2, t2	Машина 3, t3
А	13	5	9
В	5	3	7
С	6	4	5
D	7	2	6

Мы используем правило Джонсона, чтобы найти оптимальную последователь­ность. Поскольку выполнены оба условия, позволяющие применить правило Джонсона, попробуем это сделать. Вначале построим новую матрицу следующим образом.

Работа	t1 + t2	t2 + t3	Работа	t1 + t2	t2 + t3
А	18	14	С	10	9
В	8	10	D	9	8

Теперь используем правило Джонсона, как для решения проблемы N / 2, и получим оптимальную последовательность: В, А, С, D.

N работ на М машин. Когда несколько работ должны пройти через процессы на нескольких машинах или иных средствах, требуя определенных затрат времени для их выполнения, отыскание оптимальной последовательности является сложной проце­дурой.

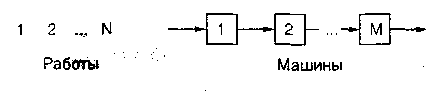
Эффективная эвристическая процедура предложена Кемпбеллом, Дюдеком и Смитом и известна под названием «CDS-алгоритм». Алгоритм CDS распространяет правило Джонсона N / 3 на общую проблему N / M и обеспечивает околооптимальное решение.

Другие исследования, которые используют теорию очередей и компьютерное моделирование (глава 5), чтобы решить сложные проблемы последовательностей математически, всегда доступны. Но все-таки что делать обыкновенному менеджеру и составителю расписаний, сталкивающимся с нахождением сложных решений поиска последовательностей запуска, которые требуют решения каждый день? Ответ такой: они должны пользоваться ординарны­ми правилами составления последовательностей обработки, та­кими, как SPT, EDD или критическим отношением. Использова­ние этих методов периодически появляется в каждом рабочем центре тогда, когда ясно, что последовательность выполнения работ изменяет экономические преимущества при движении по­тока работ от одной машины к другой. Стоит заметить, что даже если обычные подходы не ведут к оптимальным решениям, их использование на практике всегда желательно потому, что любое упорядочение всегда сопровождается положительным эффектом.

В этом смысле необходимо обратить внимание на разработки русских ученых С. А. Соколицына и В. А. Петрова, посвященные решению проблем очередности запуска. С практической точки зрения, их результативность значительно выше, чем от использо­вания ординарных правил запуска SPT, EDD и других, и в то же время процедуры, которые они предлагают, проще, чем алгоритм Кемпбелла. Правила, разработанные проф. В.А. Петровым и проф. С.А. Соколицыным, доступны для использования их менеджерами и составителями расписаний на цеховом уровне.

Формирование последовательности запуска партий дета­лей в обработку методом В. А. Петрова и С. А. Соколицына. Решение о нахождении оптимальной последовательности запуска партий деталей различных наименований отыскивалось для задан­ной одинаковой последовательности выполнения операций, т. е. для деталей с одинаковыми технологическими маршрутами обра­ботки. Детали после обработки проходили комплектацию и посту­пали на сборку. Это означает, что определялась так называемая совокупная ДПЦ обработки (Т_ЦС).

В процессе обработки партии деталей на второй и последую­щих операциях между обработкой партий различных наименова­ний возникали перерывы. Таким образом, перерывы, возникаю­щие при обработке партий деталей на последней операции, зави­сят от величин перерывов, возникающих между партиями на всех предыдущих станках, кроме первого. Это не позволяло сформулировать задачу как задачу линейного программирования, но воз­можно было аналитически сформулировать условия, которые бы обеспечивали либо отсутствие перерывов, либо их минимальную величину между обработкой деталей f-го и f + 1-го наименования на той или иной операции, кроме первой. Рис. 11.4 иллюстриру­ет движение деталей различных наименований (партий) по опе­рациям. Здесь К_Д – число наименований деталей, запускаемых в обработку; f = 1 ... К_Д ; s – число операций; j = 1 ... s.

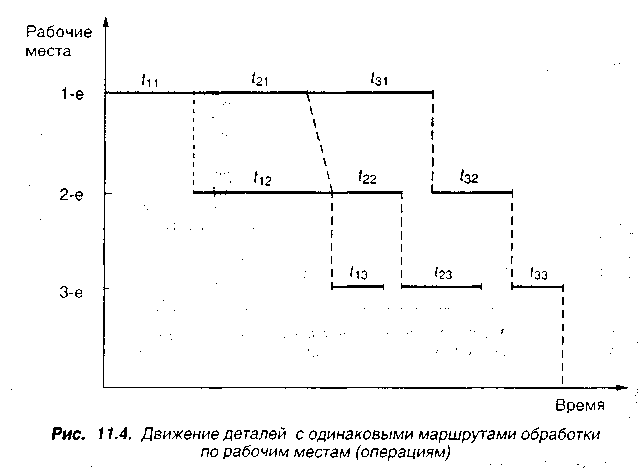
На первой операции при запуске деталей в обработку переры­вы отсутствуют, т. е. при j = 1 перерывы отсутствуют.

Рассмотрим операцию j = 2 и запишем условия, когда переры­вы отсутствуют:

между первой и второй деталью

(t₁₂ – t₂₁ ) ≥ 0 ;

между второй и третьей деталью

(t₁₂ – t₂₁) + (t₂₂ – t₃₁ ) ≥ 0 ;

и т. д.;

между (К_Д – 1) и К_Д деталью

(t₁₂ – t₂₁ ) + (t₂₂ – t₃₁ ) + ... + (t_{Кд – 1, 2} – t_{Кд, 1}) ≥ 0 .

Просуммируем условия отсутствия перерывов на операции j - 2.

(К_Д – 1) (t₁₂ – t₂₁) + (К_Д – 2) (t₂₂ – t₃₁) + ... + (t_{Кд – 1, 2} – t_{Кд, 1}) ≥ 0 .

Аналогичные условия записываем для всех операций j = 3 ... s – 1. Для j = s получим:

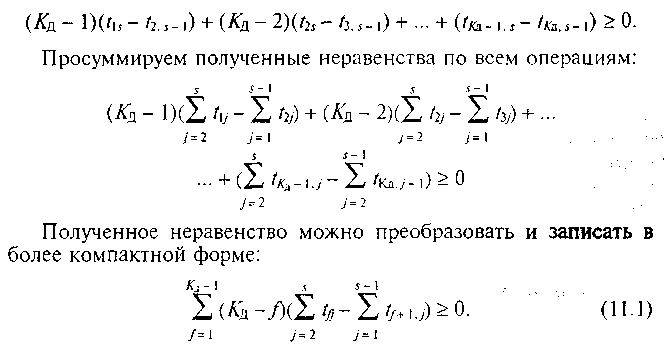
Неравенство (11.1) дает возможность сформулировать два пра­вила очередности запуска деталей в обработку, обеспечивающих минимальное значение T_ЦС:

1) детали должны обрабатываться в порядке уменьшения сум­марной трудоемкости обработки от второго до последнего станка;

2) детали должны обрабатываться в порядке увеличения сум­марной трудоемкости обработки от первого до предпоследнего станка.

ПРИМЕР 9

Формирование последовательности запуска в обработку деталей A, Б, В и Г на четырех станках в соответствии с правилами: 1) в порядке уменьшения суммарной трудоемкости обработки от второго до последнего станка; 2) в порядке увеличения суммарной трудоемкости от первого до предпоследнего станка.

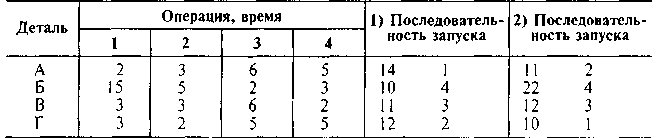
Таким образом, в соответствии с правилом 1) последовательность запуска де­талей А—Г—В—Б; правило 2) дает такую последовательность запуска: Г—А—В—Б.

Этих двух вариантов запуска бывает недостаточно. Из выраже­ния (11.1) видно, что для всех деталей, кроме f = 1 и f = K_Д , разность соответствующих сумм трудоемкости определяет собой разность длительности обработки партии на последней (j = s) и первой операциях (f = 1). Отсюда возникает третье правило: детали обрабатываются в порядке уменьшения разности трудоемкостей обработки партии на последнем и первом станках, кроме деталей первого и последнего наименования. Когда полученная разность отрицательна, то приходят к четвертому правилу, согласно кото­рому рассматривается модуль разности трудоемкостей, организо­ванных по третьему правилу.

Рассмотренный эвристический метод установления очеред­ности запуска партий деталей в обработку позволяет из громадно­го множества всех вариантов отобрать на основе сформулирован­ных правил всего четыре варианта запуска, которые в дальнейшем необходимо оценить по значению Т_ЦС.