Пример 6

Сегодня 25–й день производственного расписания. Имеется определенный порядок выполнения работ, указанный ниже.

Работа	Дата выполнения	Остающиеся рабочие дни выполнения (завершения)
А	30	4
В	28	5
С	27	2

Рассчитаем критические отношения, используя формулу CR.

Работа	Критическое отношение	Приоритетный порядок
А	(30 – 25) / 4 = 1.25	3
В	(28 – 25) / 5 = .60	1
С	(27 – 25) / 2 = 1.00	2

Работа В имеет критическое отношение меньше единицы. Выполнение се запаздывает, если не ускорить ее продвижение, поэтому она должна иметь наивыс­ший приоритет. Работа С выполняется по графику, и работа А имеет некоторый запас времени согласно сроку завершения.

Правило критического отношения может оказать помощь при решении ряда вопросов, возникающих при составлении произ­водственных расписаний в следующих системах:

1. определение статуса специфических работ;

2. определение относительных приоритетов среди работ на общей базе;

3. установление связи между величиной запаса на складе и порядком выполнения работ, находящихся в рабочем процессе на общей базе;

4. регулирование приоритетов (и пересмотр расписаний) авто­матически как при изменении, так и при возникновении прогрес­са в выполнении работ;

5. динамичное размещение работы и прослеживание пути ее выполнения.

Правило Джонсона: расписание N работ на два станка (две машины). Следующим шагом, усложняющим цеховые проблемы, является случай, в котором N работ (где N состоит из двух или более работ) должны пройти дне машины или дна рабочих центра в одинаковом порядке. Это называется проблемой N / 2.

Правило Джонсона может быть использовано для минимизации общего времени процесса обработки путем поиска последователь­ности запуска группы работ через две единицы оборудования. Оно также минимизирует общее время простоев машин (рабочих цент­ров, станков, оборудования, аппаратуры и пр.).

Правило Джонсона включает четыре шага.

1. Все работы должны быть перечислены, и представлены все требуемые времена выполнения работ на машинах.

2. Отбирается работа с наикратчайшим временем выполнения. Если наикратчайшее время приходится на первую машину, работу расписываем первой. Если наикратчайшее время приходится на вторую машину, записываем ее в расписание последней. При равенстве времен – на основе арбитражного суждения.

3. Если работа расписана, она исключается из рассмотрения.

4. Распространяются шаги 2 и 3 на оставшиеся работы при продвижении в направлении середины формирующейся последо­вательности.

ПРИМЕР 7

Пять специальных работ должны быть выполнены в двух рабочих центрах последовательно (сверлильный станок и токарный станок). Время выполнения каждой работы показано ниже.

Время процесса выполнения работ, ч

Работа	Рабочий центр (сверление)	Рабочий центр (токарная обработка)
А	5	2
В	3	б
С	8	4
D	10	7
Е	7	12

1. Мы желаем найти последовательность запуска, которая минимизирует общее время процесса обработки пяти работ. Работа с наикратчайшим временем процесса выполнения есть А в рабочем центре 2 (время выполнения два часа).

Поскольку это второй центр, работа А должна попасть в расписание последней. Исключим ее из дальнейшего рассмотрения.

А

2. Работа В – следующая с наикратчайшим временем. Поскольку оно прихо­дится на первый рабочий центр, записываем ее в списке первой и исключаем из дальнейшего рассмотрения.

В

А

3. Следующее наикратчайшее время принадлежит работе С и достигается оно на втором станке. Она расписывается так поздно, как это возможно, т. е. второй от конца.

В

С

А

4. Наблюдается равенство (семь часов) наикратчайших времен работ среди оставшихся. Мы должны разместить Е, демонстрирующую минимум в первом рабочем центре первой. Затем D на последней свободной позиции последователь­ности.

В

Е

D

С

А

Временная последовательность следующая:

Рабочий центр 1	3	7	10	8	5
Рабочий центр 2	6	12	7	4	2

Временная фазовая характеристика потока для установленной последователь­ности иллюстрируется следующим графиком.

Таким образом, пять работ завершены за 35 часов. Второй рабочий центр будет ожидать первую работу в течение трех часов, и он также будет простаивать один час после завершения работы В.

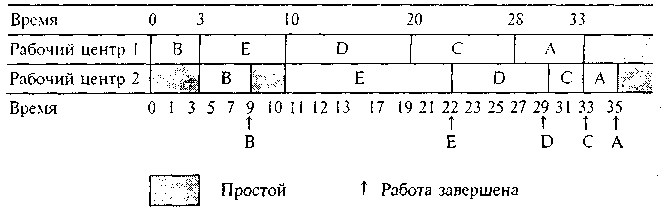
Расписание N работ на три станка (машины). Хотя оптималь­ное расписание N работ по трем машинам является чрезвычайно сложным, но если одно из двух или оба следующих условия выполнены, то решение возможно по правилу Джонсона.

1. Наименьшая продолжительность, выполняемая на машине 1, является такой большой, как наибольшая продолжительность, выполняемая на машине 2.

2. Наименьшая продолжительность выполнения работы на машине 3 по крайней мере так велика, как наиболее продолжи­тельное выполнение работы на машине 2.

Проиллюстрируем это следующим примером.