2. Составление расписаний

Целью составления расписаний является оптимизация исполь­зования ресурсов так, чтобы генеральные цели производства были достигнуты. В главном процедура расписания состоит из назначе­ния должных дат для специфических работ (ведущих).

Как упоминалось ранее, многие работы могут претендовать на использование ресурсов одновременно. Поломки машин, невыхо­ды на работу, проблемы качества, дефициты и другие факторы осложняют условия производства. Поэтому назначение даты (чис­ла) не дает уверенности, что работа будет представлена в соответ­ствии с расписанием. Создание желаемых для выполнения в срок работ расписаний требует набора правил для того, чтобы опреде­лить последовательность, в которой расписываемые работы долж­ны выполняться. Когда люди верят в эти правила и используют их, составление расписаний становится надежным и формальным средством коммуникаций.

Может использоваться много методов составления расписа­ний. Используемый тип (метод) зависит от объемов заказов, природы организаций и преобладающей сложности работ. Выбор метода также зависит от широты системы контроля над работами, представляющими производственный процесс. Например, мы мо­жем поставить цель минимизировать или ограничить время про­стоев машин, на которых выполняются дорогостоящие операции, и в то же время мы можем захотеть минимизировать стоимость заделов, находящихся в производственном процессе. Методы со­ставления расписаний делятся на две категории:

• встречное расписание;

• расписание в обратном порядке (обратное расписание).

На практике часто отмечается комбинация эти двух категорий расписаний.

Встречное расписание. Встречное расписание предполагает, что поставка материалов и выполнение операций начинается сразу же, как только становятся известны потребности в них.

Встречное расписание используется в компаниях, изготавлива­ющих металлургическую продукцию и инструменты для машино­строительных предприятий, где работы выполняются в соответст­вии с потребностями покупателей и доставка осуществляется так быстро, как это возможно. Встречное расписание хорошо подхо­дит для случаев, где поставщик обычно находится за пределами (после) расписания. Логика опережающего (встречного) расписа­ния обычно является причиной образования излишних заделов внутри производственного процесса.

Расписание в обратном порядке. В процедуре обратного расписания последняя операция процесса изготовления входит в расписание первой (расписывается первой). Затем остальные опе­рации сводятся во времени в обратном порядке в соответствии с возникающей необходимостью. В результате этой процедуры по­лучают время начала процесса. Обратное расписание хорошо работает в среде, окружающей MRP, и используется для опреде­ления запусков работ по цехам и времени выполнения ведущих операций и их последовательностей.

11.3. Загрузка цехов (рабочих центров)

Загрузка означает назначение работ, которые должны быть выполнены конкретными рабочими центрами или центрами, обеспечивающими выполнение конкретных процессов. Операци­онные менеджеры (мастера) создают рабочие центры для выпол­нения работ, обеспечивая тем самым снижение затрат, время простоев, время комплектации. Загрузка центров представлена двумя формами. Первая ориентирована на мощность центра, вторая имеет дело с назначениями специфических работ в соот­ветствующие рабочие центры. Вначале мы подвергаем проверке загрузку центра, исходя из перспектив мощности, используя для этого метод, известный под названием «контроль “вход – вы­ход”». Затем рассмотрим два подхода, используемых при загруз­ке – загрузочные графики Гантта и метод назначений в виде постановки и решения задачи линейного программирования.

Контроль «вход – выход». Многие фирмы имеют трудности при составлении расписаний (в достижении эффективного про­хождения) потому, что они перегружают производственный про­цесс. Это часто происходит потому, что они не знают действи­тельного состояния (возможностей) дел в рабочих центрах. Эф­фективное расписание зависит от подгонки расписания под со­стояние объекта. Недостаток знаний о мощности и состоянии центра является причиной, снижающей прохождение материаль­ного потока.

Контроль «вход – выход» является техникой (методом), позво­ляющей операционному персоналу гибко управлять протеканием рабочих процессов. Если работа прибывает (приходит) быстрее, чем это было предписано, значит, растут заделы. Если работа прибывает (приходит) с меньшей скоростью поступления, чем это было предусмотрено, рабочий центр может вообще выйти из графика и нарушить выполнение заказа.

Предыдущий случай (называемый перегрузкой) создает пере­полнение оборудования, ведущее к проблемам неэффективности и качества. Следующий за этим случай с недогрузкой оборудова­ния имеет своим результатом недоиспользованные мощности и потерянные ресурсы. Пример 1 иллюстрирует использование кон­троля «вход – выход».

ПРИМЕР 1

Информация в рассматриваемом примере указывает запланированную мощ­ность (загрузку) для дробильного рабочего центра на 10 недель (с 1–й по 10–ю неделю). Запланированный вход составляет 280 стандартных (нормативных) часов в неделю. Действительный вход, наиболее близкий к этой цифре, варьируется между 250 и 285. Выход, согласно составленному расписанию, определен в 320 нормативных часов и представляет предполагаемую мощность. В рабочем центре существует резерв (задел) в 300 часов¹ однако действительный выход (270 часов), по существу, меньше, чем запланированный. Поэтому ни входной план, ни выходной план не могут быть реализованы. Действительно, рабочий задел в этом центре увеличился на пять часов к 4–й неделе. Это увеличение текущего задела осложняет задачи расписания и указывает на необходимость активных действий со стороны менеджера.

Ниже приводится процедура контроля «вход – выход» для рабочего центра дробления (в нормо–часах).

Окончания недель	6/6	6/13	6/20	6/27	7/4	7/11	7/18	7/25	8/1	8/8
Планируемый выход	280	280	280	280	280	280	280	280	280	280
Действительный выход	270	250	280	285	280	285
Отклонение нарастающим итогом	–10	–40	–40	–35	–35	–30
Планируемый выход	320	320	320	320
Действительный выход	270	270	270	270
Отклонение нарастающим итогом	–50	–100	–150	–200
Изменение задела нарастающим итогом	0	–20	–10	+5

Средства, доступные оперативному персоналу, необходимые для управления рабочим потоком (процессом), следующие.

1. Корректировка представления о состоянии центра.

2. Увеличение размеров и количества оборудования.

3. Увеличение или уменьшение входа рабочего центра, для чего:

а) строго маршрутировать работу в центре или из других рабо­чих центров;

б) увеличивать пли уменьшать субконтракты;

в) производить меньше (или производить больше).

Производить меньше не является популярным решением для многих менеджеров, однако преимущества могут быть неожидан­ными. Во–первых, уровень покупательского сервиса может улуч­шиться потому, что заказы могут производиться вовремя. Во–вто­рых, эффективность может быть действительно повышена потому, что уменьшение работы устраняет загромождения и беспорядок в центре, которые увеличивали дополнительные сверхнеобходимые затраты. В–третьих, качество может повыситься, так как становит­ся меньше невыявленных проблем.

Графики Гантта. Графики Гантта являются видимым (нагляд­ным) пособием, которое полезно при загрузке и составлении расписания работ в цехе (рабочем центре). Их название произо­шло от имени Генри Гантта, который развил концепцию построения графиков в конце 1800–х годов. Графики помогают описать использование ресурсов, таких, как рабочие центры и сверхуроч­ное время.

Когда их используют для целей загрузки, графики Гантта показывают рабочее время (время занятости) и время простоев, например, нескольких отделов, машин или аппаратуры. Это по­казывает относительную рабочую занятость (загрузку) системы. Например, когда один из рабочих центров становится перегру­женным, служащие из низкозагруженного центра могут быть временно переведены в перегруженный, для повышения произ­водственной мощности перегруженного центра. Или ожидающие выполнения работы могут быть распределены по другим рабочим центрам, причем некоторые работы из высокозагруженных цент­ров могут быть переданы в центры, загруженные не полностью. Гибкое многостороннее оборудование также может быть распре­делено между центрами. Пример 2 иллюстрирует простой загру­зочный график Гантта.

ПРИМЕР 2

Производитель стиральных машин взял специальные заказы на машины, которые должны использоваться в уникальных системах, таких, как подводные лодки, госпитали и большие индустриальные прачечные. Производство каждой машины требует решения различных задач и различных времен исполнения. Рис. 1 1.2 показывает загрузочный график на неделю с 8 марта.

На четырех центрах выполняются работы в течение недели. Из карты видно, что центры по металлообработке и покраске загружены полностью на протяжении всей недели. Центры механики и электрики имеют простои, разбросанные по различным дням недели. Обращаем внимание, что центр металлообработки выве­ден из процесса во вторник, возможно, для профилактических работ.

Рис. 11.2. Загрузочный график Гантта на неделю с 8 марта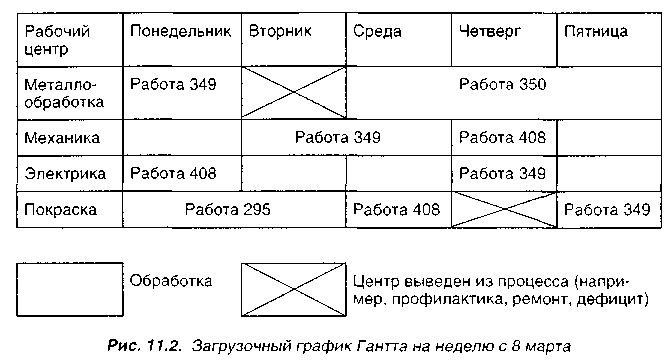

Загрузочный график Гантта имеет несколько главных ограни­чений по использованию. Одно из них: он не учитывает разнооб­разия производственных ситуаций, таких, как поломки или чело­веческие ошибки, которые требуют повторения работы. График должен также регулярно пересчитываться при появлении новых работ и при пересмотре временных оценок.

Временной график Гантта используется для управления рабо­тами в процессе. Он указывает, какая работа выполняется по расписанию и какая опережает его или отстает от расписания. Существует много возможностей использования графиков на практике. В примере 3 рассматривается временной график, разме­щающий работы по ходу их выполнения на вертикальной оси и время их выполнения на горизонтальной оси.

ПРИМЕР 3

Корпорация использует график Гантта, представленный на рис. 11.3, чтобы проследить расписание выполнения трех заказанных работ: А. В и С. Каждая пара скобок на временной оси обозначает оценку начала и окончания работы, заклю­ченной внутри них. Сплошная полоса отражает действительное положение или прогресс в выполнении работы. Работа А, например, около половины дня отстает от расписания пятого дня выполнения работы. Работа В завершена после дневной профилактики, которая была произведена до начала работы. Работа С опережает расписание.

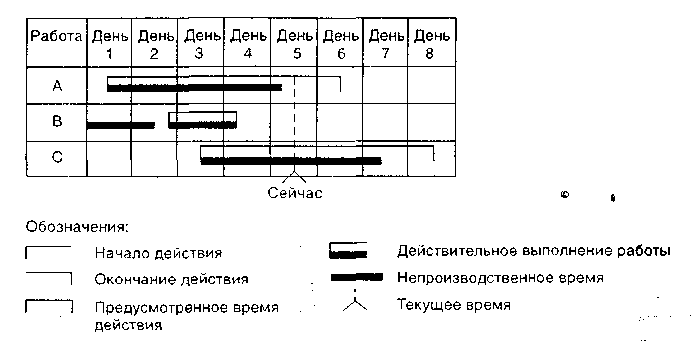
Рис. 11.3. Временной график Гантта для работ А, В и С

Метод назначений. Метод назначений представляет специаль­ный класс моделей линейного программирования, в которых рассматриваются задачи назначений и работ в зависимости от ресурсов. Примеры включают назначения работ по станкам, кон­трактов по строителям, людей по проектам и продавцов по территориям. Наиболее часто целью является достижение минимума суммарных денежных затрат или времени, необходимых для прак­тической реализации возникающих задач. Одной важной характе­ристикой проблем назначения является то, что назначению под­лежит только одна работа (или рабочий) на одну машину (или проект).

Каждая задача назначения может быть представлена таблицей. Числа в таблице будут денежными затратами или временными, ассоциирующимися с каждым конкретным назначением. Напри­мер, если в цехе имеются три свободных машины (А, В и С) и три новых работы, которые должны быть размещены, то ситуация может быть представлена таблицей.

Долларовые записи (занесения) представляют опенки фирмой затрат при назначении соответствующей работы на определенную машину.

Метод назначений – включает операции сложения и вычитания соответствующих чисел таблицы для того, чтобы найти самые низкие затраты, соответствующие условиям каждого отдельного назначения. Он включает следующие четыре шага.

1. Вычесть наименьшее число в каждой строке из каждого числа строки и затем вычесть наименьшее число в каждой колон­ке из всех чисел этой колонки.

Машина	Работа
	А	В	С
R – 34	$11	$14	$6
S – 66	$8	$10	$11
Т – 50	$9	$12	$7

Этот шаг имеет своей целью понизить величины чисел в таблице до появления в ней серии нулей. Хотя числа и изменились в результате снижения их значений, в целом проблема остается эквивалентной исходной (первоначальной) и ее оптимальное ре­шение будет тем же, что и для исходной задачи.

2. Используя минимальное число вертикальных и горизон­тальных прямых линий, необходимо зачеркнуть все нули в табли­це. Если число линий равно либо числу строк, либо числу столб­цов в таблице, тогда мы можем сделать оптимальное назначение (смотри шаг 4). Если число линий меньше числа строк или ; столбцов, мы переходим к шагу 3.

3. Вычтем минимальное неперечеркнутое число из всех других неперечеркнутых чисел. Добавим это же самое число ко всем числам, лежащим на пересечении любых двух линий. Вернемся к шагу 2 и продолжим процедуру до получения оптимального назначения.

4. Оптимальные назначения всегда будут находиться на местах размещения нулей в таблице. Направленный путь оценки назна­чений состоит в начальном отборе строки или колонки, которая содержит только один ноль. Мы можем сделать назначение в этот квадрат и затем прочеркнуть линиями эту строку и столбец. Мы осуществим это назначение и продолжим вышеописанную проце­дуру, пока не назначим каждого человека или машину в соответствии с задачей.

ПРИМЕР 4

Найдем минимальную стоимость назначения для выполнения работ на стан­ках за четыре шага. Исходные цифры взяты из предыдущей таблицы.

Машина	Работа
	А	В	С
R – 34	$11	$14	$6
S – 66	$8	$10	$11
Т – 50	$9	$12	$7

Шаг la. Используя данную таблицу, вычтем минимальное число каждой строки из каждого числа в строке. Результат будет следующий.

Машина	Работа
	А	В	С
R – 34	5	8	0
S – 66	0	2	3
Т – 50	2	5	0

Шаг 16. Вычтем минимальное число каждой колонки из каждого числа в колонке. Результат будет следующий.

Машина	Работа
	А	В	С
R – 34	5	6	0
S – 66	0	0	3
Т – 50	2	3	0

Шаг 2. Зачеркнем минимальным числом прямых линий все нули. Поскольку только две линии пересекают таблицу, решение не является оптимальным.

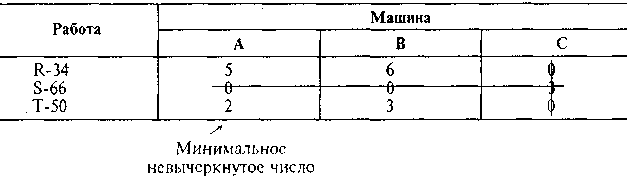
Шаг 3. Вычтем минимальное нсзачеркнутое число (2 в этой таблице) из каждого незачеркнутого числа и прибавим его к числам, находящимся на пересе­ чении двух линий.

Машина	Работа
	А	В	С
R – 34	3	4	0
S – 66	0	0	5
Т – 50	0	1	0

Вернемся к шагу 2. Покроем нули прямыми линиями снова.

Поскольку для этого необходимы три линии, то может быть сделано оптималь­ное назначение (шаг 4 на стр. 254). Назначение: R – 34 на машину С, S – 66 на машину В, Т – 50 на машину А.

(Минимальные затраты) = $6 + $10 + $9 = $25.

(Замечание: если бы мы назначили S – 66 на машину А, мы не смогли бы назначить Т – 50 на место, обозначаемое нулем.)

Некоторые задачи назначения определяют порядок макси­мизации выручки, эффективности или увольнений. Очень легко получить эквивалент минимизационной проблеме, превращая каждое число в таблице в условия потерь. Чтобы представить (осуществить) такое превращение, мы вычтем каждое число в исходной таблице увольнений из наибольшего числа в таблице.

Затем проделаем первый шаг четырехшагового метода решения проблемы назначения. В результате, минимизируя условия по­терь, получаем то же назначение, какое соответствует проблеме максимизации.