4. Жазық қималардың геометриялық сипаттамалары

Тапсырма шарты. Күрделі қима швеллерден, қоставрдан, тік төртбұрышты қимадан және тең бүйірлі бұрыштамадан құралған (7 сурет).

Кесте 3 - №3 есептеп-жобалау жұмысының сандық мәндері

Нұсқалар	Тік төртбұрыш		Қоставр	Швеллер	Бұрыштама
	h	δ		[ N	в×в×d
	мм	мм
1-20	160	10	10	16	125х125х16
21-40	220	30	16	20	160х160х18
41-60	300	15	20	24	220х220х16
61-80	250	15	16	30	100х100х10
81-100	150	10	18	22	180х180х20
101-120	200	10	20	10	200х200х20
121-140	250	12	18	20	160х160х20
141-160	300	40	14	24	125х125х16
161-180	200	14	16	18	140х140х10

Талап етіледі:

1. Қиманың ауырлық центрінің орнын анықтау;

2. Қиманың ауырлық центрі арқылы өтетін және өстеріне байланысты өстік және центрден тепкіш инерция моментерін анықтау;

3. Басты орталық инерция өстерінің орындарын анықтау;

4. Қиманың ең үлкен және кіші өстік инерция моменттерін анықтау;

5. Қиманы 1:2 маштабымен сызып, сызба барлық өлшемдерді және өстерді көрсету.

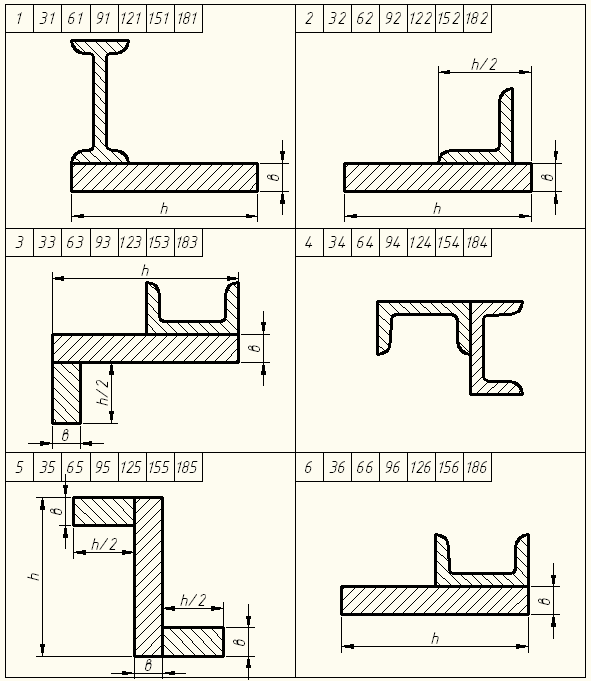
Сурет 7 - №3 есептеп-жобалау жұмысының есептеу сұлбалары

7 суреттің жалғасы

7 суреттің жалғасы

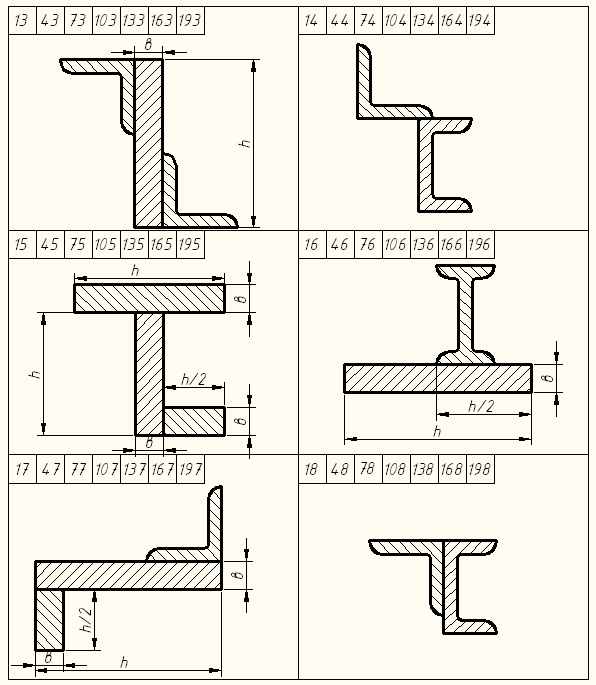
7 суреттің жалғасы

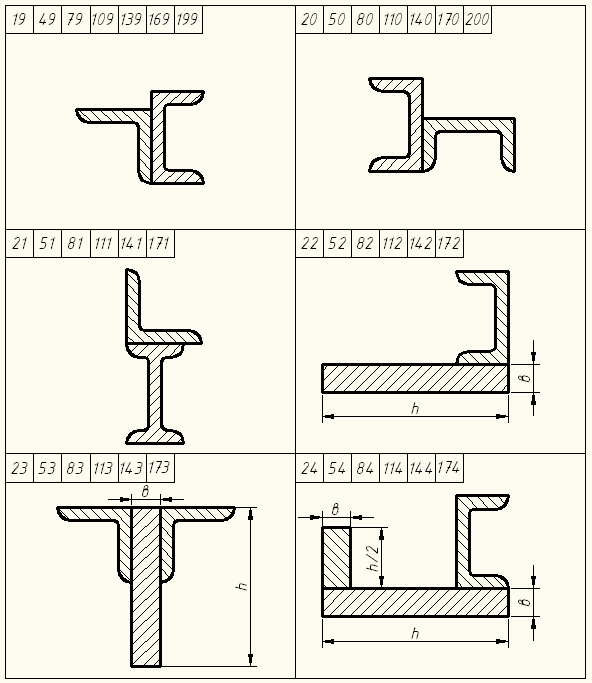
7 суреттің жалғасы

4.1 Есеп шығаруға арналған әдістемелік нұсқаулар

а) Мемлекеттік стандарт кестелерінен сызбадағы прокат профильдеріне қажетті және геометриялық сиппатамаларды жазып алу керек;

б) Қиманы 1:2 маштабымен А4 форматына сызып, оның қажетті өлшемдері көрсетіледі;

в) Күрделі қима қарапайым дара фигураларға бөлініп, оның кез келген нүктесі арқылы көмекші немесе «кездейсоқ» координат өстері Z_o, Y_o жүргізіледі;

г) Z_o , Y_o, өстеріне байланысты әр фигураның ауырлық центрінің орындары (С₁, С₂, С_i) анықталып, олар арқылы көмекші өстерге Z_o , Y_o паралелль жеке өстері Z_i , Y_i жургізіледі;

д) Күрделі қиманың ауырлық центрінің координаталары Z_с және Y_с қосымша өстерге Z_o және Y_o байланысты анықталып, графикалық жолмен тексеріледі;

е) Сызбада күрделі қиманың ауырлық центрі арқылы қосымша өстерге Z_о және Y_о паралелль орталық Z_с және Y_с өстері жүргізіледі;

ж) Әр фигураның ауырлық центрінің координаталары a_i , b_i Z_с және Y_c өстеріне өстеріне байланысты анықталып, сызбада көрсетіледі;

з) Күрделі қиманың Z_c және Y_c өстеріне байланысты өстік инерция , және центрден тепкіш инерция моменттері анықталады;

ЕСКЕРТУ! Өстік инерция моментерінің мәні әр уақытта оң танбалы «+», ал центрден тепкіш инерция моментінің мәні - теріс «-» немесе оң «+» болуы мүмкін.

и) Қиманың басты орталық инерция өстерінің U, V орындары α₁ , α₂ анықталады. Егер α > 0 болса, онда бұрыштың мәні Z_c және Y_c өстеріне сағат тіліне қарсы бағытта, ал α < 0 – сағат тілі бағытында салынады;

к) Өстік инерция моменті үлкен басты орталық инерция өсі Z_c немесе Y_c өстерімен кіші бұрыш жасайды. Мысалы: егер > , болса, онда U өсі мен Zc өсінің арасындағы бұрыш – кіші сүйір бұрыш, ал U- ең үлкен басты орталық инерция өсі;

л) Инерция моментерінің ең үлкен мәндері , есептеледі;

м) U және V өстеріне байланысты басты инерция моменттерінің , мәндерінің анықталуы тексеріледі. Дұрыстық шарты =0.